
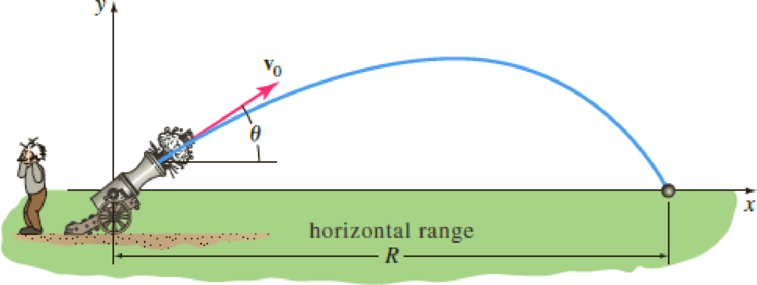
Range of a Projectile—No Air Resistance (a) A projectile, such as the canon ball shown in Figure 7.R.13, has weight w = mg and initial velocity v0 that is tangent to its path of motion. If air resistance and all other forces except its weight are ignored, we saw in Problem 23 of Exercises 4.9 that motion of the projectile is described by the system of linear differential equations
Use the Laplace transform to solve this system subject to the initial conditions
where v0 = |v0| is constant and θ is the constant angle of elevation shown in Figure 7.R.13 on page 330. The solutions x(t) and y(t) are parametric equations of the trajectory of the projectile.
- (b) Use x(t) in part (a) to eliminate the parameter t in y(t). Use the resulting equation for y to show that the horizontal range R of the projectile is given by
- (c) From the formula in part (b), we see that R is a maximum when sin 2θ = 1 or when θ = π/4. Show that the same range—less than the maximum—can be attained by firing the gun at either of two complementary angles θ and π/2 − θ. The only difference is that the smaller angle results in a low trajectory whereas the larger angle gives a high trajectory.
- (d) Suppose g = 32 ft/s2, θ = 38°, and v0 = 300 ft/s. Use part (b) to find the horizontal range of the projectile. Find the time when the projectile hits the ground.
- (e) Use the parametric equations x(t) and y(t) in part (a) along with the numerical data in part (d) to plot the ballistic curve of the projectile. Repeat with θ = 52° and v0 = 300 ft/s. Superimpose both curves on the same
coordinate system .
FIGURE 7.R.13 Projectile in Problem 51
Want to see the full answer?
Check out a sample textbook solution
Chapter 7 Solutions
Differential Equations with Boundary-Value Problems
- Prove by mathematical induction that for any positive integer n, the sum of the cubes of the first n natural numbers is given by: n Σκ k=1 (n(n + 1))²arrow_forward1 L'Ina (ln x) 2020 dx 0arrow_forwardCalibri BIUAAAA ויו Text in Italian is not being checked. Do you want to add it as a proofing language? Task 12 Fig 1 75 75 75 Fig 2 Fig 3j Add Figures 1 to 3 each shows a top view and a front view of models. Make use of the lineated paper for isometric projection and take each block on the paper as being 10mm x 10mm. Use the indicated sizes and draw an isometric view of each of the three models Samsung Galaxy A04earrow_forward
- a) show that the empty set and sigletonset are convex set. 6) show that every sub space of linear space X is convex but the convers heed not be true. c) let Mand N be two convex set of a linear Space X and KEF Show that MUN is conevex and (ii) M-N is convex or hot A and is MSN or NSM show that MUN convex or not, 385arrow_forwardxp x+xarrow_forwardFor the given graph, determine the following. -3 12 УА 4 3 - -1 ° 1 2 3 x -1. -2- a. Determine for which values of a the lim f (x) exists but f is not continuous at x = a. a b. Determine for which values of a the function is continuous but not differentiable at x = a. aarrow_forward
- I write with prove one-to-one linear Sanction but not onto Lexample.) b) write with Prove on to linear function but not oh-to-on (example). c) write with prove example x=y St Xandy two linear space over Sielad F.arrow_forwardUse the following graph of ƒ (x) to evaluate ƒ' (−1) and ƒ' (2). y +10+ 9 8 7 6 5 4 3 2 1- -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 x 3 4 0 8 9 10 -2 3 -4 5 -6 -7 -8 -9 -10- f'(-1)= f' (2)arrow_forwardFor the following function f and real number a, a. find the slope of the tangent line mtan = = f' (a), and b. find the equation of the tangent line to f at x = a. f(x) = 2 = ;a=2 a. Slope: b. Equation of tangent line: yarrow_forward
 Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
 Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning, Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education





