EXERCISES In Exercises 1–3, assume that you work for the Internal Revenue Service. You are asked to write a report about the claim that 57% of U.S. adults think the amount of federal income tax they pay is too high. (Source: Gallup) 1. What is the null hypothesis in this situation? Describe how your report could be incorrect by trying to prove the null hypothesis. 2. Describe how your report could make a type I error. 3. Describe how your report could make a type II error.

Question

Want to see more full solutions like this?

Answer 1

Textbook Question

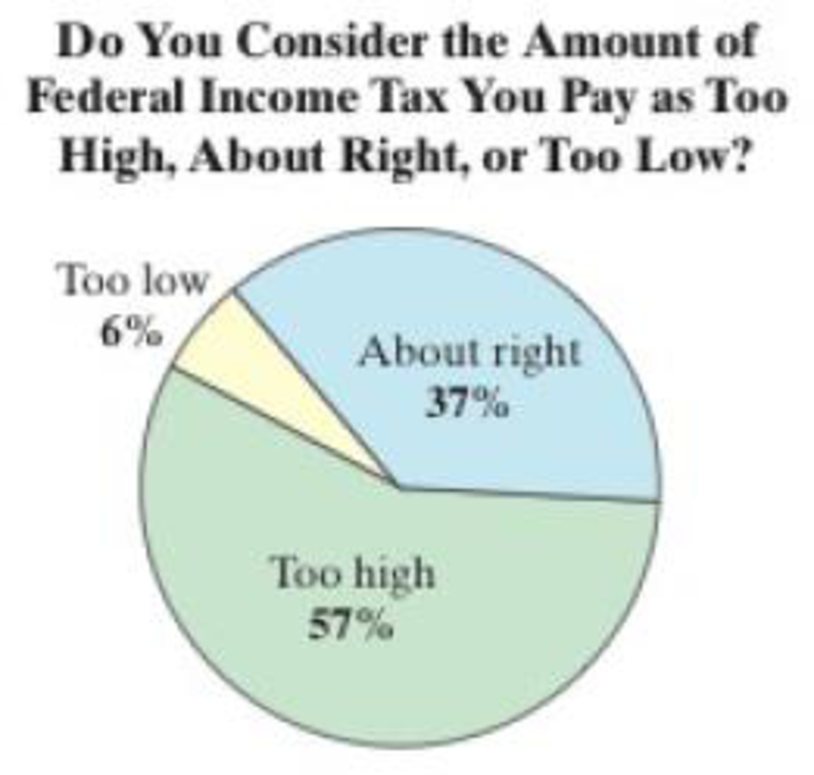
Chapter 7, Problem 1UA

EXERCISES

In Exercises 1–3, assume that you work for the Internal Revenue Service. You are asked to write a report about the claim that 57% of U.S. adults think the amount of federal income tax they pay is too high. (Source: Gallup)

1. What is the null hypothesis in this situation? Describe how your report could be incorrect by trying to prove the null hypothesis.
2. Describe how your report could make a type I error.
3. Describe how your report could make a type II error.

Chapter 7, Problem 1UA, EXERCISES In Exercises 13, assume that you work for the Internal Revenue Service. You are asked to

Expert Solution & Answer

To determine

To state: The null hypothesis in the given situation and describe how the report could be incorrect by trying to prove the null hypothesis.

Answer to Problem 1UA

The null hypothesis in the given situation is, H0:p=0.57 .

When type error is present, the report could be incorrect by trying to prove the null hypothesis.

Explanation of Solution

Null hypothesis:

Null hypothesis is a statement about the population parameter. Its value is equal to the claim value, which is denoted by H0 . The population parameter can be the mean, standard deviation, proportion, variance, and so forth. The possible symbols used in the null hypothesis would be ≤,≥ or = .

Alternative hypothesis:

It is complementary to the null hypothesis. That is, it differs from the null hypothesis. The possible symbols used in the alternative hypothesis would be <,>, or ≠. It is denoted by H1 .

Here, the claim is that, “57% of U.S adults think the amount of federal income tax they pay is too high”. This can be written as p=0.57 . The complement of the claim is p≠0.57 .

Null hypothesis: H0:p=0.57

Type I error: Rejecting the null hypothesis, when it is actually true.

Type II error: Failing to reject the null hypothesis, when it is false.

A type I error occurs when the hypothesis test indicates that the percentage of U.S. adults think the amount of federal income tax they pay is too high is not 57%; but in reality, the percentage of U.S. adults think the amount of federal income tax they pay is too high is 57%. Thus, the report could be incorrect by trying to prove the null hypothesis when the type error I is present.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Students have asked these similar questions

08:34 ◄ Classroom 07:59 Probs. 5-32/33 D ا. 89 5-34. Determine the horizontal and vertical components of reaction at the pin A and the normal force at the smooth peg B on the member. A 0,4 m 0.4 m Prob. 5-34 F=600 N fr th ar 0. 163586 5-37. The wooden plank resting between the buildings deflects slightly when it supports the 50-kg boy. This deflection causes a triangular distribution of load at its ends. having maximum intensities of w, and wg. Determine w and wg. each measured in N/m. when the boy is standing 3 m from one end as shown. Neglect the mass of the plank. 0.45 m 3 m

Examine the Variables: Carefully review and note the names of all variables in the dataset. Examples of these variables include: Mileage (mpg) Number of Cylinders (cyl) Displacement (disp) Horsepower (hp) Research: Google to understand these variables. Statistical Analysis: Select mpg variable, and perform the following statistical tests. Once you are done with these tests using mpg variable, repeat the same with hp Mean Median First Quartile (Q1) Second Quartile (Q2) Third Quartile (Q3) Fourth Quartile (Q4) 10th Percentile 70th Percentile Skewness Kurtosis Document Your Results: In RStudio: Before running each statistical test, provide a heading in the format shown at the bottom. “# Mean of mileage – Your name’s command” In Microsoft Word: Once you've completed all tests, take a screenshot of your results in RStudio and paste it into a Microsoft Word document. Make sure that snapshots are very clear. You will need multiple snapshots. Also transfer these results to the…

Answer 2

Textbook Question

Chapter 7, Problem 1UA

EXERCISES

In Exercises 1–3, assume that you work for the Internal Revenue Service. You are asked to write a report about the claim that 57% of U.S. adults think the amount of federal income tax they pay is too high. (Source: Gallup)

1. What is the null hypothesis in this situation? Describe how your report could be incorrect by trying to prove the null hypothesis.
2. Describe how your report could make a type I error.
3. Describe how your report could make a type II error.

Chapter 7, Problem 1UA, EXERCISES In Exercises 13, assume that you work for the Internal Revenue Service. You are asked to

Expert Solution & Answer

To determine

To state: The null hypothesis in the given situation and describe how the report could be incorrect by trying to prove the null hypothesis.

Answer to Problem 1UA

The null hypothesis in the given situation is, H0:p=0.57 .

When type error is present, the report could be incorrect by trying to prove the null hypothesis.

Explanation of Solution

Null hypothesis:

Null hypothesis is a statement about the population parameter. Its value is equal to the claim value, which is denoted by H0 . The population parameter can be the mean, standard deviation, proportion, variance, and so forth. The possible symbols used in the null hypothesis would be ≤,≥ or = .

Alternative hypothesis:

It is complementary to the null hypothesis. That is, it differs from the null hypothesis. The possible symbols used in the alternative hypothesis would be <,>, or ≠. It is denoted by H1 .

Here, the claim is that, “57% of U.S adults think the amount of federal income tax they pay is too high”. This can be written as p=0.57 . The complement of the claim is p≠0.57 .

Null hypothesis: H0:p=0.57

Type I error: Rejecting the null hypothesis, when it is actually true.

Type II error: Failing to reject the null hypothesis, when it is false.

A type I error occurs when the hypothesis test indicates that the percentage of U.S. adults think the amount of federal income tax they pay is too high is not 57%; but in reality, the percentage of U.S. adults think the amount of federal income tax they pay is too high is 57%. Thus, the report could be incorrect by trying to prove the null hypothesis when the type error I is present.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Answer 3

Textbook Question

Chapter 7, Problem 1UA

EXERCISES

In Exercises 1–3, assume that you work for the Internal Revenue Service. You are asked to write a report about the claim that 57% of U.S. adults think the amount of federal income tax they pay is too high. (Source: Gallup)

1. What is the null hypothesis in this situation? Describe how your report could be incorrect by trying to prove the null hypothesis.
2. Describe how your report could make a type I error.
3. Describe how your report could make a type II error.

Chapter 7, Problem 1UA, EXERCISES In Exercises 13, assume that you work for the Internal Revenue Service. You are asked to

Expert Solution & Answer

To determine

To state: The null hypothesis in the given situation and describe how the report could be incorrect by trying to prove the null hypothesis.

Answer to Problem 1UA

The null hypothesis in the given situation is, H0:p=0.57 .

When type error is present, the report could be incorrect by trying to prove the null hypothesis.

Explanation of Solution

Null hypothesis:

Null hypothesis is a statement about the population parameter. Its value is equal to the claim value, which is denoted by H0 . The population parameter can be the mean, standard deviation, proportion, variance, and so forth. The possible symbols used in the null hypothesis would be ≤,≥ or = .

Alternative hypothesis:

It is complementary to the null hypothesis. That is, it differs from the null hypothesis. The possible symbols used in the alternative hypothesis would be <,>, or ≠. It is denoted by H1 .

Here, the claim is that, “57% of U.S adults think the amount of federal income tax they pay is too high”. This can be written as p=0.57 . The complement of the claim is p≠0.57 .

Null hypothesis: H0:p=0.57

Type I error: Rejecting the null hypothesis, when it is actually true.

Type II error: Failing to reject the null hypothesis, when it is false.

A type I error occurs when the hypothesis test indicates that the percentage of U.S. adults think the amount of federal income tax they pay is too high is not 57%; but in reality, the percentage of U.S. adults think the amount of federal income tax they pay is too high is 57%. Thus, the report could be incorrect by trying to prove the null hypothesis when the type error I is present.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Answer 4

Textbook Question

Chapter 7, Problem 1UA

EXERCISES

In Exercises 1–3, assume that you work for the Internal Revenue Service. You are asked to write a report about the claim that 57% of U.S. adults think the amount of federal income tax they pay is too high. (Source: Gallup)

1. What is the null hypothesis in this situation? Describe how your report could be incorrect by trying to prove the null hypothesis.
2. Describe how your report could make a type I error.
3. Describe how your report could make a type II error.

Chapter 7, Problem 1UA, EXERCISES In Exercises 13, assume that you work for the Internal Revenue Service. You are asked to

Expert Solution & Answer

To determine

To state: The null hypothesis in the given situation and describe how the report could be incorrect by trying to prove the null hypothesis.

Answer to Problem 1UA

The null hypothesis in the given situation is, H0:p=0.57 .

When type error is present, the report could be incorrect by trying to prove the null hypothesis.

Explanation of Solution

Null hypothesis:

Null hypothesis is a statement about the population parameter. Its value is equal to the claim value, which is denoted by H0 . The population parameter can be the mean, standard deviation, proportion, variance, and so forth. The possible symbols used in the null hypothesis would be ≤,≥ or = .

Alternative hypothesis:

It is complementary to the null hypothesis. That is, it differs from the null hypothesis. The possible symbols used in the alternative hypothesis would be <,>, or ≠. It is denoted by H1 .

Here, the claim is that, “57% of U.S adults think the amount of federal income tax they pay is too high”. This can be written as p=0.57 . The complement of the claim is p≠0.57 .

Null hypothesis: H0:p=0.57

Type I error: Rejecting the null hypothesis, when it is actually true.

Type II error: Failing to reject the null hypothesis, when it is false.

A type I error occurs when the hypothesis test indicates that the percentage of U.S. adults think the amount of federal income tax they pay is too high is not 57%; but in reality, the percentage of U.S. adults think the amount of federal income tax they pay is too high is 57%. Thus, the report could be incorrect by trying to prove the null hypothesis when the type error I is present.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Answer 5

Textbook Question

Answer 6

Textbook Question

Answer 7

Expert Solution & Answer

To determine

To state: The null hypothesis in the given situation and describe how the report could be incorrect by trying to prove the null hypothesis.

Answer to Problem 1UA

The null hypothesis in the given situation is, H0:p=0.57 .

When type error is present, the report could be incorrect by trying to prove the null hypothesis.

Explanation of Solution

Null hypothesis:

Null hypothesis is a statement about the population parameter. Its value is equal to the claim value, which is denoted by H0 . The population parameter can be the mean, standard deviation, proportion, variance, and so forth. The possible symbols used in the null hypothesis would be ≤,≥ or = .

Alternative hypothesis:

It is complementary to the null hypothesis. That is, it differs from the null hypothesis. The possible symbols used in the alternative hypothesis would be <,>, or ≠. It is denoted by H1 .

Here, the claim is that, “57% of U.S adults think the amount of federal income tax they pay is too high”. This can be written as p=0.57 . The complement of the claim is p≠0.57 .

Null hypothesis: H0:p=0.57

Type I error: Rejecting the null hypothesis, when it is actually true.

Type II error: Failing to reject the null hypothesis, when it is false.

A type I error occurs when the hypothesis test indicates that the percentage of U.S. adults think the amount of federal income tax they pay is too high is not 57%; but in reality, the percentage of U.S. adults think the amount of federal income tax they pay is too high is 57%. Thus, the report could be incorrect by trying to prove the null hypothesis when the type error I is present.

Answer 8

Expert Solution & Answer

To determine

To state: The null hypothesis in the given situation and describe how the report could be incorrect by trying to prove the null hypothesis.

Answer to Problem 1UA

The null hypothesis in the given situation is, H0:p=0.57 .

When type error is present, the report could be incorrect by trying to prove the null hypothesis.

Explanation of Solution

Null hypothesis:

Null hypothesis is a statement about the population parameter. Its value is equal to the claim value, which is denoted by H0 . The population parameter can be the mean, standard deviation, proportion, variance, and so forth. The possible symbols used in the null hypothesis would be ≤,≥ or = .

Alternative hypothesis:

It is complementary to the null hypothesis. That is, it differs from the null hypothesis. The possible symbols used in the alternative hypothesis would be <,>, or ≠. It is denoted by H1 .

Here, the claim is that, “57% of U.S adults think the amount of federal income tax they pay is too high”. This can be written as p=0.57 . The complement of the claim is p≠0.57 .

Null hypothesis: H0:p=0.57

Type I error: Rejecting the null hypothesis, when it is actually true.

Type II error: Failing to reject the null hypothesis, when it is false.

A type I error occurs when the hypothesis test indicates that the percentage of U.S. adults think the amount of federal income tax they pay is too high is not 57%; but in reality, the percentage of U.S. adults think the amount of federal income tax they pay is too high is 57%. Thus, the report could be incorrect by trying to prove the null hypothesis when the type error I is present.

Answer 9

Expert Solution & Answer

Answer 10

Expert Solution & Answer

Answer 11

To determine

To state: The null hypothesis in the given situation and describe how the report could be incorrect by trying to prove the null hypothesis.

Answer 12

Answer to Problem 1UA

The null hypothesis in the given situation is, H0:p=0.57 .

When type error is present, the report could be incorrect by trying to prove the null hypothesis.

Answer 13

Explanation of Solution

Null hypothesis:

Null hypothesis is a statement about the population parameter. Its value is equal to the claim value, which is denoted by H0 . The population parameter can be the mean, standard deviation, proportion, variance, and so forth. The possible symbols used in the null hypothesis would be ≤,≥ or = .

Alternative hypothesis:

It is complementary to the null hypothesis. That is, it differs from the null hypothesis. The possible symbols used in the alternative hypothesis would be <,>, or ≠. It is denoted by H1 .

Here, the claim is that, “57% of U.S adults think the amount of federal income tax they pay is too high”. This can be written as p=0.57 . The complement of the claim is p≠0.57 .

Null hypothesis: H0:p=0.57

Type I error: Rejecting the null hypothesis, when it is actually true.

Type II error: Failing to reject the null hypothesis, when it is false.

A type I error occurs when the hypothesis test indicates that the percentage of U.S. adults think the amount of federal income tax they pay is too high is not 57%; but in reality, the percentage of U.S. adults think the amount of federal income tax they pay is too high is 57%. Thus, the report could be incorrect by trying to prove the null hypothesis when the type error I is present.

Answer 14

Ch. 7.1 - Write each claim as a mathematical statement....Ch. 7.1 - A company specializing in parachute assembly...Ch. 7.1 - For each claim, state H0 and Ha in words and in...Ch. 7.1 - You perform a hypothesis test for each claim. How...Ch. 7.1 - 1. You represent a chemical company that is being...Ch. 7.1 - What are the two types of hypotheses used in a...Ch. 7.1 - Describe the two types of errors possible in a...Ch. 7.1 - Prob. 3E Ch. 7.1 - Does failing to reject the null hypothesis mean...Ch. 7.1 - True or False? In Exercises 510, determine whether...

Concept explainers

Videos

Answer to Problem 1UA

Explanation of Solution

Want to see more full solutions like this?

Chapter 7 Solutions