
Concept explainers
(a)
Interpretation: A process flow diagram is to be constructed along withlabeling and the times and percentages.
Concept Introduction:
Any flow unit, when flows through a process, follows L’s Law which states that the Work in Progress and given by,
(a)
Explanation of Solution
Process flow diagram is as follows.

(b)
Interpretation: The throughout in patients is to be determined per hour of each stage in the process.
Concept Introduction:
The throughput of any process is the rate at which outputs are coming out of the process. When the capacity (i.e. the service rate) of a process step is more than or equal to the arrival rate or the demand rate, the throughput will be equal to the demand rate.
On the contrary, if the capacity is less than the demand rate, it means that the process step is a bottleneck and the throughput will be equal to the capacity.
(b)
Explanation of Solution
The throughout in patients per hour of each stage in the process is shown in table below.
| Resource | Demand or arrival rate | Capacity or Service rate | Condition | Throughout rate |
| RC | 10 per hour | 10 per hour | ||
| RRC | 10 per hour | 10 per hour | ||
| NP | 10 per hour | 10 per hour | ||
| PA | 4 per hour | |||
| MD | 4 per hour | |||
| BC | 8 per hour | 8 per hour |
(c)
Interpretation: The labor utilization rates are to be calculated and whether these values appropriate. In case they are not appropriate the way the process can be redesigned is to be determined along with then bottlenecks.
Concept Introduction:
The labor utilization is defined as the fraction of time a resource is busy producing output in the long run. It can be calculated by using the following formula.
(c)
Explanation of Solution
However, note that the labor utilization cannot be more than 100% in long run. However, in short run, we can write it as more than 100% using the above formula.
| Resource | Demand or arrival rate | Capacity or Service rate | Number of servers (N) | Utilization (U) |
| RC | 10 per hour | 1 | 50.00% | |
| RRC | 10 per hour | 1 | 100.00% | |
| NP | 10 per hour | 1 | 83.33% | |
| PA | 1 | 40.00% | ||
| MD | 1 | 150.00% | ||
| BC | 8 per hour | 1 | 66.67% |
The resource RRC and MD are overloaded as the utilization figures suggest. Similarly, the resource RC and PA are under loaded. Possible improvement strategy is to share the loads of work (as they are similar in nature) between RC and RRC. Also, it should be checked whether the 60/40 ratio of diversion to MD and PA can be modified in order to balance their load
At present, the resource MD, having the capacity less than the arrival rate and thus the flow is constrained at MD. So, it is the bottleneck.
(d)
Interpretation: The way by which the given change affect your answer to the preceding questions.
Concept Introduction:
Any flow unit, when flows through a process, follows L’s Law which states that the Work in Progress and given by,
(d)
Explanation of Solution
Due to the change, the process layout will be as follows.
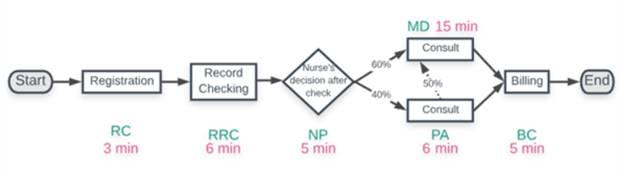
The throughput rates for each resource will be as follows.
| Resource | Demand or arrival rate (D) | Capacity or Service rate | Condition | Throughout rate |
| RC | 10 per hour | 10 per hour | ||
| RRC | 10 per hour | 10 per hour | ||
| NP | 10 per hour | 10 per hour | ||
| PA | 4 per hour | |||
| MD | 4 per hour | |||
| BC | 6 per hour |
The labor utilization of the resources are as follows.
| Resource | Demand or arrival rate | Capacity or Service rate | Number of servers (N) | Utilization (U)
|
| RC | 10 per hour | 1 | 50.00% | |
| RRC | 10 per hour | 1 | 100.00% | |
| NP | 10 per hour | 1 | 83.33% | |
| PA | 1 | 40.00% | ||
| MD | 1 | 200.00% | ||
| BC | 1 | 50.00% |
Note that the utilization of MD has just jumped to 200%.
Want to see more full solutions like this?
Chapter 7 Solutions
OM (with OM Online, 1 term (6 months) Printed Access Card)
- At Quick Car Wash, the wash process is advertised to take less than 6 minutes. Consequently, management has set a target average of 330 seconds for the wash process. Suppose the average range for a sample of 7 cars is 10 seconds. Use the accompanying table to establish control limits for sample means and ranges for the car wash process. Click the icon to view the table of factors for calculating three-sigma limits for the x-chart and R-chart. The UCLR equals seconds and the LCLR equals seconds. (Enter your responses rounded to two decimal places.)arrow_forwardIf Jeremy who is the VP for the operations, proceeds with their existing prototype (which is option a), the firm can then expect sales to be 120,000 units at $550 each. And with a probability of 0.52 and a 0.48 probability of 65,000 at $550. we However, he uses his value analysis team (option b), the firm expects sales of 75,000 units at $770, with a probability of 0.78 and a 0.22 probability of 65,000 units at $770. Value engineering, at a cost of $100,000, is only used in option b. Which option for this has the highest expected monetary value (EMV)? The EMV for option a is $? The EMV for option b is $? Which has the highest expected monetary value. A or B?arrow_forwardPart 1 of 2 Jim's Outfitters, Inc., makes custom western shirts. The shirts could be flawed in various ways, including flaws in the weave or color of the fabric, loose buttons or decorations, wrong dimensions, and uneven stitches. Jim randomly examined 10 shirts, with the following results shown to the right. Shirt Defects 1 7 2 1 4 13 3 10 2 8 5 9 10 8 7 a. Assuming that 10 observations are adequate for these purposes, determine the three-sigma control limits for defects per shirt. The UCLC equals and the LCL equals (Enter your responses rounded to two decimal places. If your answer for LCL is negative, enter this value as 0.)arrow_forward
- Management at Webster Chemical Company is concerned as to whether caulking tubes are being properly capped. If a significant proportion of the tubes are not being sealed, Webster is placing its customers in a messy situation. Tubes are packaged in large boxes of 144. Several boxes are inspected, and the following numbers of leaking tubes are found: Sample Tubes Sample Tubes Sample Tubes 1 7 8 7 15 7 2 7 9 8 16 9 3 6 10 7 17 3 4 4 11 1 18 7 5 8 12 8 19 7 6 7 2 9 13 14 1 20 6 7 Total 121 Calculate p-chart three-sigma control limits to assess whether the capping process is in statistical control. The UCLp equals and the LCLp equals (Enter your responses rounded to three decimal places. If your answer for LCLp is negative, enter this value as 0.)arrow_forwardAspen Plastics produces plastic bottles to customer order. The quality inspector randomly selects four bottles from the bottle machine and measures the outside diameter of the bottle neck, a critical quality dimension that determines whether the bottle cap will fit properly. The dimensions (in.) from the last six samples are Bottle Sample 1 2 3 4 1 0.624 0.586 0.602 0.591 2 0.613 0.599 0.578 0.618 3 0.606 0.585 0.587 0.623 4 0.581 0.623 0.571 0.610 5 0.609 0.610 0.623 0.617 6 0.605 0.573 0.570 0.602 Click the icon to view the table of factors for calculating three-sigma limits for the x-chart and R-chart. Suppose that the specification for the bottle neck diameter is 0.600 ± 0.050 in. and the population standard deviation is 0.014 in. a. What is the process capability index? The Cpk is (Enter your response rounded to two decimal places.)arrow_forwardHow would you handle the Apple 'batterygate' scandal as an operations manager? What quality measures would you take to fix the problem and prevent it from happening again? When would you implement these measures and communicate with the stakeholders?arrow_forward
- Perosnal Thoughts about the articlearrow_forwardRevenue retrieval for Brew Mini= $ round response to two decimal places What would be the best design alternative? Brew master or brew miniarrow_forwardThe revenue retrieval for PG Glass design is ?. Enter response as a whole number). The revenue retrieval for Glass Unlimited design is ? (enter your response as a whole number). What is The best design alternative? Glass unlimited or PG Glass?arrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,MarketingMarketingISBN:9780357033791Author:Pride, William MPublisher:South Western Educational Publishing
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,MarketingMarketingISBN:9780357033791Author:Pride, William MPublisher:South Western Educational Publishing


