
Concept explainers
A multiple-choice exam has 100 questions. Each question has four choices, (a) What minimum score should be required to reduce the chance of passing by random guessing to 5 percent? (b) To 1 percent? (c) Find the
a.
Find the minimum score should be required to reduce the chance of passing by random guessing to 5%.
Answer to Problem 107CE
The minimum score should be required to reduce the chance of passing by random guessing to 5% is 32.12.
Explanation of Solution
Calculation:
It is given that a multiple-choice exam has 100 questions, with 4 options each.
Assume that the random variable X defines the number of correct answers by a student randomly guessing the answers. Consider choosing a correct answer as a success. Then, X has a binomial distribution.
Only 1 out of the 4 options is correct for each question. Thus, the probability of success is
Normal distribution:
A continuous random variable X is said to follow normal distribution if the probability density function of X is,
Binomial distribution:
A discrete random variable X is said to follow binomial distribution if the probability mass function is defined as,
It is known that, when
Here,
Hence,
As the conditions for approximation are satisfied, the normal approximation can be used.
The expected number of the random variable X is,
The standard deviation of the random variable X is,
The approximate normal probability that a student passes by random guessing is 5%.
Denote
Again, the probability
Variable value:
Software procedure:
Step-by-step software procedure to obtain variable value using EXCEL is as follows:
- • Open an EXCEL file.
- • In cell E1, enter the formula “=NORM.INV(0.95,25,4.33)”.
- Output using EXCEL software is given below:
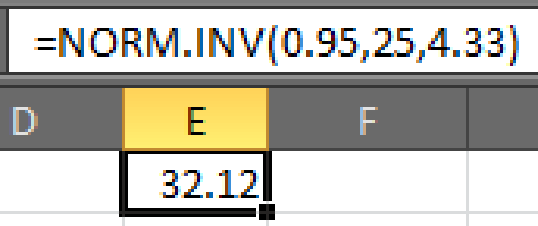
Hence,
Therefore,
Thus, the minimum score should be required to reduce the chance of passing by random guessing to 5% is 32.12.
b.
Find the minimum score should be required to reduce the chance of passing by random guessing to 1%.
Answer to Problem 107CE
The minimum score should be required to reduce the chance of passing by random guessing to 1% is 35.07.
Explanation of Solution
Calculation:
Denote
Again, the probability
Variable value:
Software procedure:
Step-by-step software procedure to obtain variable value using EXCEL is as follows:
- • Open an EXCEL file.
- • In cell E1, enter the formula “=NORM.INV(0.99,25,4.33)”.
- Output using EXCEL software is given below:
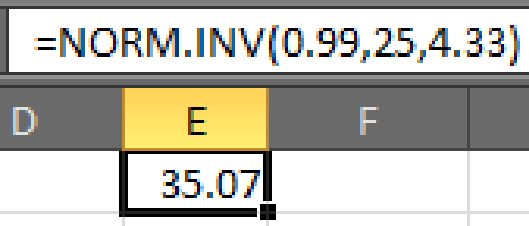
Hence,
Therefore,
Thus, the minimum score should be required to reduce the chance of passing by random guessing to 1% is 35.07.
c.
Find the quartiles for a student who guesses.
Answer to Problem 107CE
The first and third quartiles of scores for a student who guesses are respectively 22.08 and 27.92.
Explanation of Solution
Calculation:
The first quartile of a distribution is the value of the variable, below which, 25% of the observations lie. In other words, the probability that an observation lies below the first quartile is 0.25.
Denote
First quartile:
Software procedure:
Step-by-step software procedure to obtain the first quartile using EXCEL is as follows:
- • Open an EXCEL file.
- • In cell E1, enter the formula “=NORM.INV(0.25,25,4.33)”.
- Output using EXCEL software is given below:
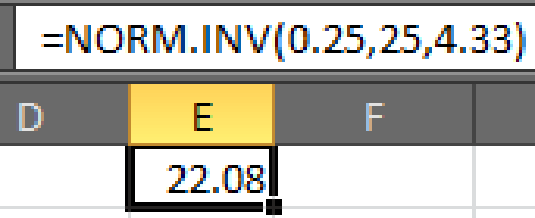
Here,
Hence,
The third quartile of a distribution is the value of the variable, below which, 75% of the observations lie. In other words, the probability that an observation lies below the third quartile is 0.75.
Denote
Third quartile:
Software procedure:
Step-by-step software procedure to obtain the third quartile using EXCEL is as follows:
- • Open an EXCEL file.
- • In cell E1, enter the formula “=NORM.INV(0.75,25,4.33)”.
- Output using EXCEL software is given below:
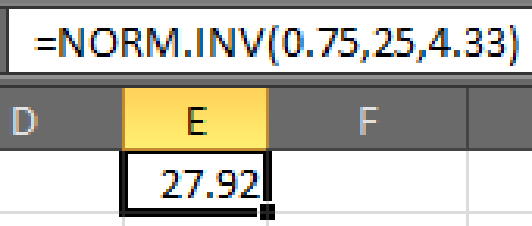
Here,
Hence,
Thus, the first and third quartiles of scores for a student who guesses are respectively 22.08 and 27.92.
Want to see more full solutions like this?
Chapter 7 Solutions
APPLIED STAT.IN BUS.+ECONOMICS
- F Make a box plot from the five-number summary: 100, 105, 120, 135, 140. harrow_forward14 Is the standard deviation affected by skewed data? If so, how? foldarrow_forwardFrequency 15 Suppose that your friend believes his gambling partner plays with a loaded die (not fair). He shows you a graph of the outcomes of the games played with this die (see the following figure). Based on this graph, do you agree with this person? Why or why not? 65 Single Die Outcomes: Graph 1 60 55 50 45 40 1 2 3 4 Outcome 55 6arrow_forward
- lie y H 16 The first month's telephone bills for new customers of a certain phone company are shown in the following figure. The histogram showing the bills is misleading, however. Explain why, and suggest a solution. Frequency 140 120 100 80 60 40 20 0 0 20 40 60 80 Telephone Bill ($) 100 120arrow_forward25 ptical rule applies because t Does the empirical rule apply to the data set shown in the following figure? Explain. 2 6 5 Frequency 3 сл 2 1 0 2 4 6 8 00arrow_forward24 Line graphs typically connect the dots that represent the data values over time. If the time increments between the dots are large, explain why the line graph can be somewhat misleading.arrow_forward
- 17 Make a box plot from the five-number summary: 3, 4, 7, 16, 17. 992) waarrow_forward12 10 - 8 6 4 29 0 Interpret the shape, center and spread of the following box plot. brill smo slob.nl bagharrow_forwardSuppose that a driver's test has a mean score of 7 (out of 10 points) and standard deviation 0.5. a. Explain why you can reasonably assume that the data set of the test scores is mound-shaped. b. For the drivers taking this particular test, where should 68 percent of them score? c. Where should 95 percent of them score? d. Where should 99.7 percent of them score? Sarrow_forward
- 13 Can the mean of a data set be higher than most of the values in the set? If so, how? Can the median of a set be higher than most of the values? If so, how? srit to estaarrow_forwardA random variable X takes values 0 and 1 with probabilities q and p, respectively, with q+p=1. find the moment generating function of X and show that all the moments about the origin equal p. (Note- Please include as much detailed solution/steps in the solution to understand, Thank you!)arrow_forward1 (Expected Shortfall) Suppose the price of an asset Pt follows a normal random walk, i.e., Pt = Po+r₁ + ... + rt with r₁, r2,... being IID N(μ, o²). Po+r1+. ⚫ Suppose the VaR of rt is VaRq(rt) at level q, find the VaR of the price in T days, i.e., VaRq(Pt – Pt–T). - • If ESq(rt) = A, find ES₁(Pt – Pt–T).arrow_forward
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning






