
Concept explainers
Derive the system of equations (1) by applying Newton’s second law,
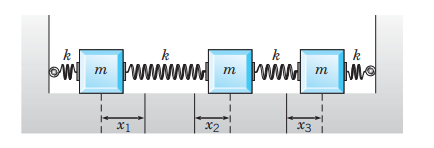
The system of equations describing motions of a three mass and four spring system by applying Newton’s second law
Answer to Problem 1P
Solution:
The system of equations describing motions of a three mass and four spring system are
Explanation of Solution
Given information:
Three masses
Newton’s second law is
The springs follow Hooke’s Law: The force exerted by a spring on a mass is directly proportional to the length of its departure from its equilibrium length.
Explanation:
The first mass’s one side is attached to the wall with the spring and the other side is attached to the second body with another spring of spring constant
Then the velocity of the mass is
Then the acceleration of the mass is
By Newton’s law, the forces acting on the mass is
By Hooke’s law, the forces acting on the mass is
Also, a force
Then the equation of motion of the first body is
In the second case, the second body is attached to the first body with the spring and the other side is attached to the third body with another spring of spring constant
Then the velocity of the mass is
Then the acceleration of the mass is
By Newton’s law, the forces acting on the mass is
By Hooke’s law, the forces acting on the mass is
Also, a force
Then the equation of motion of the second body is
Similarly, in the third case, the third mass is attached to the wall with the spring and in the other side, it is attached to the second body with another spring of spring constant
Then the velocity of the mass is
Then the acceleration of the mass is
By Newton’s law, the forces acting on the mass is
By Hooke’s law, the forces acting on the mass is
Also, a force
Then the equation of motion of the third body is
Thus, the system of equations describing the motions of a three mass and four spring system are
Want to see more full solutions like this?
Chapter 6 Solutions
Differential Equations: An Introduction To Modern Methods And Applications 3e Binder Ready Version + Wileyplus Registration Card
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
Thinking Mathematically (6th Edition)
Introductory Statistics
College Algebra with Modeling & Visualization (5th Edition)
Elementary Statistics: Picturing the World (7th Edition)
- 27 Suppose that you have a data set of 1, 2, 2, 3, 3, 3, 4, 4, 5, and you assume that this sample represents a population. The mean is 3 and g the standard deviation is 1.225.10 a. Explain why you can apply the empirical rule to this data set. b. Where would "most of the values" in the population fall, based on this data set?arrow_forward30 Explain how you can use the empirical rule to find out whether a data set is mound- shaped, using only the values of the data themselves (no histogram available).arrow_forward5. Let X be a positive random variable with finite variance, and let A = (0, 1). Prove that P(X AEX) 2 (1-A)² (EX)² EX2arrow_forward
- 6. Let, for p = (0, 1), and xe R. X be a random variable defined as follows: P(X=-x) = P(X = x)=p. P(X=0)= 1-2p. Show that there is equality in Chebyshev's inequality for X. This means that Chebyshev's inequality, in spite of being rather crude, cannot be improved without additional assumptions.arrow_forward4. Prove that, for any random variable X, the minimum of EIX-al is attained for a = med (X).arrow_forward8. Recall, from Sect. 2.16.4, the likelihood ratio statistic, Ln, which was defined as a product of independent, identically distributed random variables with mean 1 (under the so-called null hypothesis), and the, sometimes more convenient, log-likelihood, log L, which was a sum of independent, identically distributed random variables, which, however, do not have mean log 1 = 0. (a) Verify that the last claim is correct, by proving the more general statement, namely that, if Y is a non-negative random variable with finite mean, then E(log Y) log(EY). (b) Prove that, in fact, there is strict inequality: E(log Y) < log(EY), unless Y is degenerate. (c) Review the proof of Jensen's inequality, Theorem 5.1. Generalize with a glimpse on (b).arrow_forward
- 2. Derive the component transformation equations for tensors shown be- low where [C] = [BA] is the direction cosine matrix from frame A to B. B[T] = [C]^[T][C]T 3. The transport theorem for vectors shows that the time derivative can be constructed from two parts: the first is an explicit frame-dependent change of the vector whereas the second is an active rotational change of the vector. The same holds true for tensors. Starting from the previous result, derive a version of transport theorem for tensors. [C] (^[T])[C] = dt d B dt B [T] + [WB/A]B[T] – TWB/A] (10 pt) (7pt)arrow_forwardUse the graph of the function y = f (x) to find the value, if possible. f(x) 8 7 6 Q5 y 3 2 1 x -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 -1 -2 -3 -4 -5 -6 -7 -8+ Olim f(z) x-1+ O Limit does not exist.arrow_forward3. Prove that, for any random variable X, the minimum of E(X - a)² is attained for a = EX. Provedarrow_forward
- Shade the areas givenarrow_forward7. Cantelli's inequality. Let X be a random variable with finite variance, o². (a) Prove that, for x ≥ 0, P(X EX2x)≤ 02 x² +0² 202 P(|X - EX2x)<≤ (b) Find X assuming two values where there is equality. (c) When is Cantelli's inequality better than Chebyshev's inequality? (d) Use Cantelli's inequality to show that med (X) - EX ≤ o√√3; recall, from Proposition 6.1, that an application of Chebyshev's inequality yields the bound o√√2. (e) Generalize Cantelli's inequality to moments of order r 1.arrow_forwardThe college hiking club is having a fundraiser to buy new equipment for fall and winter outings. The club is selling Chinese fortune cookies at a price of $2 per cookie. Each cookie contains a piece of paper with a different number written on it. A random drawing will determine which number is the winner of a dinner for two at a local Chinese restaurant. The dinner is valued at $32. Since fortune cookies are donated to the club, we can ignore the cost of the cookies. The club sold 718 cookies before the drawing. Lisa bought 13 cookies. Lisa's expected earnings can be found by multiplying the value of the dinner by the probability that she will win. What are Lisa's expected earnings? Round your answer to the nearest cent.arrow_forward
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
