Chapter 6.3, Problem 14P

Diffusion on a One-dimensional Lattice with an Absorbing Boundary. Consider a one-dimensional lattice consisting of $n=4$ lattice points, as shown in Figure 6.3.6

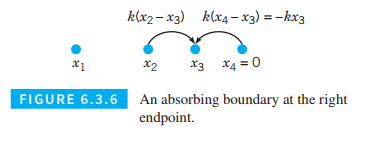
Assume that the left endpoint is a reflecting boundary so that the rate equation for the number of particles $x_1\left(t\right)$ occupying that site is given by Eq.(21). Further assume that the sites $2$ and $3$ are interior points with rate equations given by Eq.(20)but with the condition that $x_4\left(t\right)=0$ for all $t\ge 0$.

(a) Find the system of differential equations that describe the rate equation for $\text{x=}{\left(x_1,x_2,x_3\right)}^T$ and express the equations in matrix notation, $\text{x'=Ax}$.

(b) Site $4$ is referred to as an absorbing boundary because particles that land on that site from site $3$ are removed from the diffusion process. Show that

$\frac{d}{dt}\left(x_1+x_2+x_3\right)=-k{x}_3$

and explain the meaning of this equation.

(c) Find the eigenvalues and eigenvectors for the matrix $\text{A}$ in part (a) and plot the components of the eigenvectors. Then compare the eigenvalues and eigenvectors with those found in Example 3 of this section.

(d) Find the general solution of the system of equations found in part (a).Explain the asymptotic behavior of $\text{x}\left(t\right)$ as $t\to \infty$.