Mathematics For Machine Technology
8th Edition
ISBN: 9781337798310
Author: Peterson, John.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 67, Problem 2A
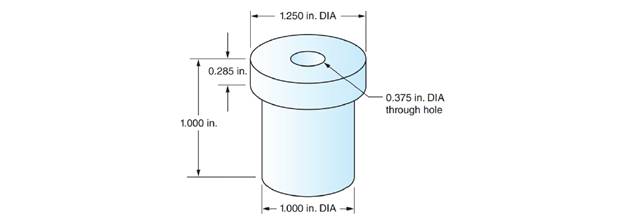
Find the number of cubic inches of material contained in the jig bushing shown. Round the answer to the nearest hundredth cubic inch.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
4. Assume that a risk-free money market account is added to the market described in Q3.
The continuously compounded rate of return on the money market account is log (1.1).
(i) For each given μ, use Lagrange multipliers to determine the proportions (as a
function of μ) of wealth invested in the three assets available for the minimum
variance portfolio with expected return μ.
(ii) Determine the market portfolio in this market and calculate its Sharp ratio.
3. A market consists of two risky assets with rates of return R₁ and R2 and no risk-free
asset. From market data the following have been estimated: ER₁ = 0.25, ER2 = 0.05,
Var R₁ = 0.01, Var R2 = 0.04 and the correlation between R1 and R2 is p = -0.75.
(i) Given that an investor is targeting a total expected return of μ = 0.2. What
portfolio weights should they choose to meet this goal with minimum portfolio
variance? Correct all your calculations up to 4 decimal points.
(ii) Determine the global minimum-variance portfolio and the expected return and
variance of return of this portfolio (4 d.p.).
(iii) Sketch the minimum-variance frontier in the μ-σ² plane and indicate the efficient
frontier.
(iv) Without further calculation, explain how the minimum variance of the investor's
portfolio return will change if the two risky assets were independent.
2. A landlord is about to write a rental contract for a tenant which lasts T months. The
landlord first decides the length T > 0 (need not be an integer) of the contract, the
tenant then signs it and pays an initial handling fee of £100 before moving in. The
landlord collects the total amount of rent erT at the end of the contract at a continuously
compounded rate r> 0, but the contract stipulates that the tenant may leave before T,
in which case the landlord only collects the total rent up until the tenant's departure
time 7. Assume that 7 is exponentially distributed with rate > 0, λ‡r.
(i) Calculate the expected total payment EW the landlord will receive in terms of T.
(ii) Assume that the landlord has logarithmic utility U(w) = log(w - 100) and decides
that the rental rate r should depend on the contract length T by
r(T)
=
λ
√T
1
For each given λ, what T (as a function of X) should the landlord choose so as to
maximise their expected utility? Justify your answer.
Hint. It might be…
Chapter 67 Solutions
Mathematics For Machine Technology
Ch. 67 - If tan A=4.13792 , determine the value of angle A...Ch. 67 - Find the number of cubic inches of material...Ch. 67 - Find the number of cubic inches of material...Ch. 67 - The sector of a circle has an area of 231.3 sq in....Ch. 67 - Determine the arc length ABC if r=5.75in. and...Ch. 67 - Identify each of the following angles as acute....Ch. 67 - Refer to the following figure in answering...Ch. 67 - Refer to the following figure in answering...Ch. 67 - Refer to the following figure in answering...Ch. 67 - Refer to the following figure in answering...
Ch. 67 - Refer to the following figure in answering...Ch. 67 - Prob. 12ACh. 67 - Refer to the following figure in answering...Ch. 67 - For each exercise, functions of two angles are...Ch. 67 - For each exercise, functions of two angles are...Ch. 67 - For each exercise, functions of two angles are...Ch. 67 - For each exercise, functions of two angles are...Ch. 67 - For each exercise, functions of two angles are...Ch. 67 - For each exercise, functions of two angles are...Ch. 67 - For each exercise, functions of two angles are...Ch. 67 - For each exercise, functions of two angles are...Ch. 67 - For each exercise, functions of two angles are...Ch. 67 - For each exercise, functions of two angles are...Ch. 67 - For each exercise, functions of two angles are...Ch. 67 - Prob. 25ACh. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - Prob. 41ACh. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - For each function of an angle, write the...Ch. 67 - Prob. 45ACh. 67 - For each exercise, functions and cofunctions of...Ch. 67 - Prob. 47ACh. 67 - For each exercise, functions and cofunctions of...Ch. 67 - Prob. 49ACh. 67 - For each exercise, functions and cofunctions of...Ch. 67 - Prob. 51ACh. 67 - For each exercise, functions and cofunctions of...Ch. 67 - Prob. 53ACh. 67 - For each exercise, functions and cofunctions of...Ch. 67 - Prob. 55ACh. 67 - For each exercise, functions and cofunctions of...Ch. 67 - Prob. 57A
Additional Math Textbook Solutions
Find more solutions based on key concepts
The largest polynomial that divides evenly into a list of polynomials is called the _______.
Elementary & Intermediate Algebra
1. How much money is Joe earning when he’s 30?
Pathways To Math Literacy (looseleaf)
True or False The quotient of two polynomial expressions is a rational expression, (p. A35)
Precalculus
23. A plant nursery sells two sizes of oak trees to landscapers. Large trees cost the nursery $120 from the gro...
College Algebra (Collegiate Math)
Let F be a continuous distribution function. If U is uniformly distributed on (0,1), find the distribution func...
A First Course in Probability (10th Edition)
1. How is a sample related to a population?
Elementary Statistics: Picturing the World (7th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Please ensure that all parts of the question are answered thoroughly and clearly. Include a diagram to help explain answers. Make sure the explanation is easy to follow. Would appreciate work done written on paper. Thank you.arrow_forwardConsider the proof below: Proposition: If m is an even integer, then 5m +4 is an even integer. Proof: We see that |5m+4=10n+4 = 2(5n+2). Therefore, 5m+4 is an even integer. **Note: you may assume the proof is valid, just poorly written. Based upon the Section 1.3 screencast and the reading assignment, select all writing guidelines that are missing in the proof. Proof begins by stating assumptions ✓ Proof has an invitational tone/uses collective pronouns Proof is written in complete sentences Each step is justified ☐ Proof has a clear conclusionarrow_forwardThe general solution X'=Ax is given. Discuss the nature of the solutions in a neighborhood of (0,0) -2-2 (²) |a) A = (23) X(A) = (₁ (fi)e* + (2 (2) eht -2-5arrow_forward
- Please ensure that all parts of the question are answered thoroughly and clearly. Include a diagram to help explain answers. Make sure the explanation is easy to follow. Would appreciate work done written on paper. Thank you.arrow_forwardUsing the method of joints, determine the force in each member of the truss shown. Summarize the results on a force summation diagram, and indicate whether each member is in tension or compression. You may want to try the "quick" method hod.16 8m T or C CD CE AB EF BF гид B 6m i force in CE only (change top force to 8kn) 8 KN 8kNarrow_forwardNo chatgpt pls will upvotearrow_forward
- Please ensure that all parts of the question are answered thoroughly and clearly. Include a diagram to help explain answers. Make sure the explanation is easy to follow. Would appreciate work done written on paper. Thank you.arrow_forwardI just need help with f and garrow_forwardPlease ensure that all parts of the question are answered thoroughly and clearly. Include a diagram to help explain answers. Make sure the explanation is easy to follow. Would appreciate work done written on paper. Thank you.arrow_forward
- You are coming home hungry and look in your fridge. You find: 1 roll and 2 slices of bread, a jar ofpeanut butter, one single serve package each of mayo and mustard, a can of cheezewhiz, some slicedham, and some sliced turkey. How many different types of (edible) sandwiches can you make? Writedown any assumptions (order matters or not, repetitons allowed or not).arrow_forwardAlready got wrong chatgpt answer Plz don't use chatgpt answer will upvotearrow_forward7. Suppose that X is a set, that I is a nonempty set, and that for each i Є I that Yi is a set. Suppose that I is a nonempty set. Prove the following:2 (a) If Y; CX for all i EI, then Uiel Yi C X. ¹See Table 4.8.1 in zyBooks. Recall: Nie X₁ = Vi Є I (x = X₁) and x = Uier X₁ = i Є I (x Є Xi). (b) If XCY; for all i Є I, then X Ciel Yi. (c) U(x)=xnUY. iЄI ΕΙarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, 
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Use of ALGEBRA in REAL LIFE; Author: Fast and Easy Maths !;https://www.youtube.com/watch?v=9_PbWFpvkDc;License: Standard YouTube License, CC-BY
Compound Interest Formula Explained, Investment, Monthly & Continuously, Word Problems, Algebra; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=P182Abv3fOk;License: Standard YouTube License, CC-BY
Applications of Algebra (Digit, Age, Work, Clock, Mixture and Rate Problems); Author: EngineerProf PH;https://www.youtube.com/watch?v=Y8aJ_wYCS2g;License: Standard YouTube License, CC-BY