Introduction to Statistics and Data Analysis
5th Edition
ISBN: 9781305750999
Author: Peck Olson Devore
Publisher: CENGAGE C
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 6.4, Problem 42E
The paper “Good for Women, Good for Men, Bad for People: Simpson’s Paradox and the Importance of Sex-Specific Analysis in Observational Studies” (Journal of Women’s Health and Gender-Based Medicine [2001]: 867-872) described the results of a medical study in which one treatment was shown to be better for men and better for women than a competing treatment. However, if the data for men and women are combined, it appears as though the competing treatment is better.
To see how this can happen, consider the accompanying data tables constructed from information in the paper. Subjects in the study were given either Treatment A or Treatment B, and survival was noted. Let S be the
- a. The following table summarizes data for men and women combined:
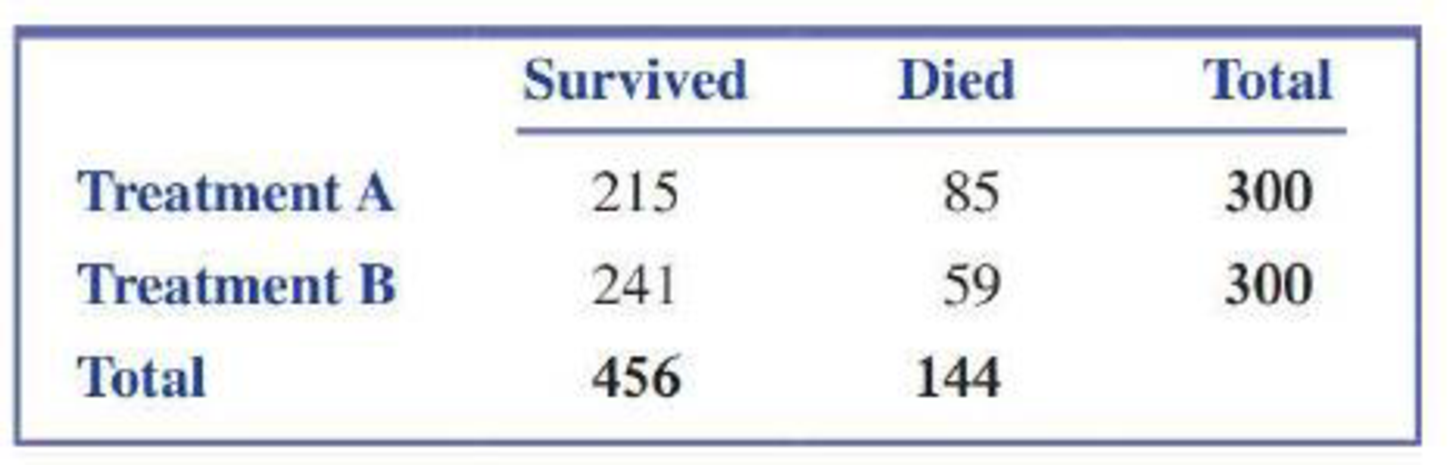
- i. Find P(S).
- ii. Find P(S|A).
- iii. Find P(S|B).
- iv. Which treatment appears to be better?
- b. Now consider the summary data for the men who participated in the study:
- v. Find P(S).
- vi. Find P(S|A).
- vii. Find P(S|B).
- viii. Which treatment appears to be better?
- c. Now consider the summary data for the women who participated in the study:
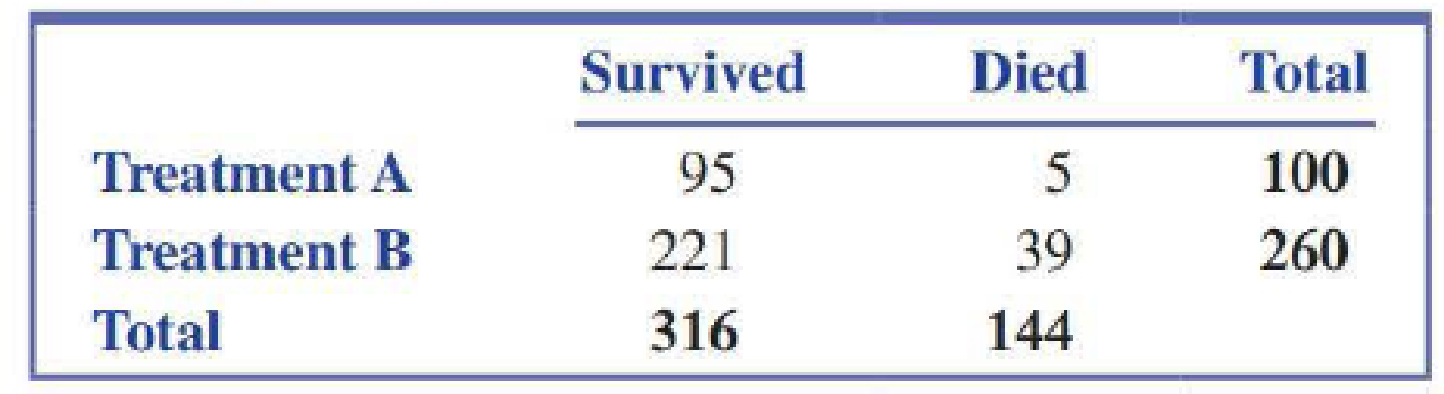
- ix. Find P(S). looks like Treatment B is better. This is an
- x. Find P(S|A).
- xi. Find P(S|B).
- xii. Which treatment appears to be better?
- d. You should have noticed from Parts (b) and (c) that for both men and women, Treatment A appears to be better. But in Part (a), when the data for men and women are combined, it looks like Treatment B is better. This is an example of what is called Simpson’s paradox. Write a brief explanation of why this apparent inconsistency occurs for this data set. (Hint: Do men and women respond similarly to the two treatments?)
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
The following are suggested designs for group sequential studies. Using PROCSEQDESIGN, provide the following for the design O’Brien Fleming and Pocock.• The critical boundary values for each analysis of the data• The expected sample sizes at each interim analysisAssume the standardized Z score method for calculating boundaries.Investigators are evaluating the success rate of a novel drug for treating a certain type ofbacterial wound infection. Since no existing treatment exists, they have planned a one-armstudy. They wish to test whether the success rate of the drug is better than 50%, whichthey have defined as the null success rate. Preliminary testing has estimated the successrate of the drug at 55%. The investigators are eager to get the drug into production andwould like to plan for 9 interim analyses (10 analyzes in total) of the data. Assume thesignificance level is 5% and power is 90%.Besides, draw a combined boundary plot (OBF, POC, and HP)
Please provide the solution for the attached image in detailed.
20 km, because
GISS
Worksheet 10
Jesse runs a small business selling and delivering mealie meal to the spaza shops.
He charges a fixed rate of R80, 00 for delivery and then R15, 50 for each packet of
mealle meal he delivers. The table below helps him to calculate what to charge
his customers.
10
20
30
40
50
Packets of mealie
meal (m)
Total costs in Rands
80
235
390
545
700
855
(c)
10.1.
Define the following terms:
10.1.1. Independent Variables
10.1.2. Dependent Variables
10.2.
10.3.
10.4.
10.5.
Determine the independent and dependent variables.
Are the variables in this scenario discrete or continuous values? Explain
What shape do you expect the graph to be? Why?
Draw a graph on the graph provided to represent the information in the
table above.
TOTAL COST OF PACKETS OF MEALIE MEAL
900
800
700
600
COST (R)
500
400
300
200
100
0
10
20
30
40
60
NUMBER OF PACKETS OF MEALIE MEAL
Chapter 6 Solutions
Introduction to Statistics and Data Analysis
Ch. 6.1 - Define the term chance experiment, and give an...Ch. 6.1 - Define the term sample space, and then give the...Ch. 6.1 - Consider the chance experiment in which the type...Ch. 6.1 - A tennis shop sells five different brands of...Ch. 6.1 - A new model of laptop computer can be ordered with...Ch. 6.1 - A college library has four copies of a certain...Ch. 6.1 - A library has five copies of a certain textbook on...Ch. 6.1 - Suppose that, starting at a certain time,...Ch. 6.1 - Refer to the previous exercise and now suppose...Ch. 6.1 - Prob. 10E
Ch. 6.1 - An engineering construction firm is currently...Ch. 6.1 - Consider a Venn diagram picturing two events A and...Ch. 6.3 - A large department store offers online ordering....Ch. 6.3 - The manager of a music store has kept records of...Ch. 6.3 - A bookstore sells two types of books (fiction and...Ch. 6.3 - ▼ Medical insurance status—covered (C) or not...Ch. 6.3 - Roulette is a game of chance that involves...Ch. 6.3 - Phoenix is a hub for a large airline. Suppose that...Ch. 6.3 - A professor assigns five problems to be completed...Ch. 6.3 - Refer to the following information on full-term...Ch. 6.3 - Prob. 21ECh. 6.3 - Prob. 22ECh. 6.3 - Prob. 23ECh. 6.3 - Prob. 24ECh. 6.3 - A deck of 52 playing cards is mixed well, and 5...Ch. 6.3 - Prob. 26ECh. 6.3 - The student council for a school of science and...Ch. 6.3 - A student placement center has requests from five...Ch. 6.3 - Prob. 29ECh. 6.4 - Two different airlines have a flight from Los...Ch. 6.4 - The article Chances Are You Know Someone with a...Ch. 6.4 - The accompanying data are from the article...Ch. 6.4 - The following graphical display is similar to one...Ch. 6.4 - Delayed diagnosis of cancer is a problem because...Ch. 6.4 - The events E and T are defined as E = the event...Ch. 6.4 - The newspaper article Folic Acid Might Reduce Risk...Ch. 6.4 - Suppose that an individual is randomly selected...Ch. 6.4 - Is ultrasound a reliable method for determining...Ch. 6.4 - The table at the top of the next page summarizes...Ch. 6.4 - USA Today (June 6, 2000) gave information on seal...Ch. 6.4 - Prob. 41ECh. 6.4 - The paper Good for Women, Good for Men, Bad for...Ch. 6.5 - Many fire stations handle emergency calls for...Ch. 6.5 - The paper Predictors of Complementary Therapy Use...Ch. 6.5 - The report TV Drama/Comedy Viewers and Health...Ch. 6.5 - Prob. 46ECh. 6.5 - Prob. 47ECh. 6.5 - In a small city, approximately 15% of those...Ch. 6.5 - Jeanie is a bit forgetful, and if she doesnt make...Ch. 6.5 - Prob. 50ECh. 6.5 - Prob. 51ECh. 6.5 - Prob. 52ECh. 6.5 - The following case study was reported in the...Ch. 6.5 - Three friends (A, B, and C) will participate in a...Ch. 6.5 - Prob. 55ECh. 6.5 - A store sells two different brands of dishwasher...Ch. 6.5 - The National Public Radio show Car Talk used to...Ch. 6.5 - Refer to the previous exercise. Suppose now that...Ch. 6.6 - A university has 10 vehicles available for use by...Ch. 6.6 - Prob. 60ECh. 6.6 - Prob. 61ECh. 6.6 - Let F denote the event that a randomly selected...Ch. 6.6 - According to a July 31, 2013 posting on cnn.com, a...Ch. 6.6 - Suppose that Blue Cab operates 15% of the taxis in...Ch. 6.6 - A large cable company reports the following: 80%...Ch. 6.6 - Refer to the information given in the previous...Ch. 6.6 - The authors of the paper Do Physicians Know When...Ch. 6.6 - A study of how people are using online services...Ch. 6.6 - Prob. 69ECh. 6.6 - Prob. 70ECh. 6.6 - Prob. 71ECh. 6.6 - Prob. 72ECh. 6.6 - Prob. 73ECh. 6.6 - The paper referenced in the previous exercise also...Ch. 6.6 - In an article that appears on the web site of the...Ch. 6.6 - Prob. 76ECh. 6.6 - Only 0.1% of the individuals in a certain...Ch. 6.7 - The Los Angeles Times (June 14, 1995) reported...Ch. 6.7 - Five hundred first-year students at a state...Ch. 6.7 - The table given below describes (approximately)...Ch. 6.7 - On April 1, 2010, the Bureau of the Census in the...Ch. 6 - A company uses three different assembly linesA1,...Ch. 6 - Prob. 88CRCh. 6 - Prob. 89CRCh. 6 - Prob. 90CRCh. 6 - Prob. 91CRCh. 6 - A company sends 40% of its overnight mail parcels...Ch. 6 - Prob. 93CRCh. 6 - Prob. 94CRCh. 6 - In a school machine shop, 60% of all machine...Ch. 6 - There are five faculty members in a certain...Ch. 6 - The general addition rule for three events states...Ch. 6 - A theater complex is currently showing four...Ch. 6 - Prob. 100CRCh. 6 - Suppose that a box contains 25 light bulbs, of...Ch. 6 - Prob. 102CRCh. 6 - A transmitter is sending a message using a binary...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Let X be a random variable with support SX = {−3, 0.5, 3, −2.5, 3.5}. Part ofits probability mass function (PMF) is given bypX(−3) = 0.15, pX(−2.5) = 0.3, pX(3) = 0.2, pX(3.5) = 0.15.(a) Find pX(0.5).(b) Find the cumulative distribution function (CDF), FX(x), of X.1(c) Sketch the graph of FX(x).arrow_forwardA well-known company predominantly makes flat pack furniture for students. Variability with the automated machinery means the wood components are cut with a standard deviation in length of 0.45 mm. After they are cut the components are measured. If their length is more than 1.2 mm from the required length, the components are rejected. a) Calculate the percentage of components that get rejected. b) In a manufacturing run of 1000 units, how many are expected to be rejected? c) The company wishes to install more accurate equipment in order to reduce the rejection rate by one-half, using the same ±1.2mm rejection criterion. Calculate the maximum acceptable standard deviation of the new process.arrow_forward5. Let X and Y be independent random variables and let the superscripts denote symmetrization (recall Sect. 3.6). Show that (X + Y) X+ys.arrow_forward
- 8. Suppose that the moments of the random variable X are constant, that is, suppose that EX" =c for all n ≥ 1, for some constant c. Find the distribution of X.arrow_forward9. The concentration function of a random variable X is defined as Qx(h) = sup P(x ≤ X ≤x+h), h>0. Show that, if X and Y are independent random variables, then Qx+y (h) min{Qx(h). Qr (h)).arrow_forward10. Prove that, if (t)=1+0(12) as asf->> O is a characteristic function, then p = 1.arrow_forward
- 9. The concentration function of a random variable X is defined as Qx(h) sup P(x ≤x≤x+h), h>0. (b) Is it true that Qx(ah) =aQx (h)?arrow_forward3. Let X1, X2,..., X, be independent, Exp(1)-distributed random variables, and set V₁₁ = max Xk and W₁ = X₁+x+x+ Isk≤narrow_forward7. Consider the function (t)=(1+|t|)e, ER. (a) Prove that is a characteristic function. (b) Prove that the corresponding distribution is absolutely continuous. (c) Prove, departing from itself, that the distribution has finite mean and variance. (d) Prove, without computation, that the mean equals 0. (e) Compute the density.arrow_forward
- 1. Show, by using characteristic, or moment generating functions, that if fx(x) = ½ex, -∞0 < x < ∞, then XY₁ - Y2, where Y₁ and Y2 are independent, exponentially distributed random variables.arrow_forward1. Show, by using characteristic, or moment generating functions, that if 1 fx(x): x) = ½exarrow_forward1990) 02-02 50% mesob berceus +7 What's the probability of getting more than 1 head on 10 flips of a fair coin?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Hypothesis Testing using Confidence Interval Approach; Author: BUM2413 Applied Statistics UMP;https://www.youtube.com/watch?v=Hq1l3e9pLyY;License: Standard YouTube License, CC-BY
Hypothesis Testing - Difference of Two Means - Student's -Distribution & Normal Distribution; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=UcZwyzwWU7o;License: Standard Youtube License