Algebra 1
1st Edition
ISBN: 9780078884801
Author: McGraw-Hill/Glencoe
Publisher: Glencoe/McGraw-Hill School Pub Co
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 6.3, Problem 31PPS
a.
To determine
To write the system of equations that represents the number of U.S. teams and non-U.S. teams.
a.
Expert Solution
Answer to Problem 31PPS
x+y=66x−y=30
Explanation of Solution
Given:
Number of professional mountain bike racing teams: 66
Number of non-U.S. teams is 30 more than the number of U.S. teams.
Calculation:
Let x represent the number of non-U.S. teams and y represent the number of U.S. teams.
The total number of professional mountain bike racing teams is 66.
So, it can be represented as:
x+y=66 →(1)
Also, the number of non-U.S. teams is 30 more than the number of U.S. teams. Then,
x=y+30 ⇒x−y=30 →(2)
Conclusion:
Therefore, the equations that represent the U.S. and Non-U.S. teams are
x+y=66x−y=30
b.
To determine
To find the solution to the system of equations found in (a).
b.
Expert Solution
Answer to Problem 31PPS
x=48
y=18
Explanation of Solution
Given:
From subpart (a),
The system of equations is:
x+y=66x−y=30
Calculation:
Let the equations be labelled as follows:
x+y=66 →(1)x−y=30 →(2)
Add the above equations.
x+y=66 x−y=302x=96
2x=96x=962x=48
Substitute x=48 in any of the equations.
Say, Equation (2),
48−y=30 [Subtracting 48 on both sides]−y=30−48−y=−18y=18
Conclusion:
Therefore, the solutions of the system of equations is x=48 and y=18.
c.
To determine
To interpret the solution as the context of the question
c.
Expert Solution
Answer to Problem 31PPS
Non-U.S. teams: 48
U.S. teams: 18
Explanation of Solution
Given:
From subpart (b),
x=48
y=18
Calculation:
Let x represent the number of non-U.S. teams and y represent the number of U.S. teams.
Then the number of non-U.S. teams is 48
The number of U.S. teams is 18.
Conclusion:
Therefore, the number of non-U.S. teams and U.S. teams are 48 and 18 respectively.
d.
To determine
Graph the system of equations and check the solution.
d.
Expert Solution
Explanation of Solution
Given:
From subpart (a),
The system of equations is:
x+y=66x−y=30
Graph:
Using a graphing utility the system of equations is graphed as follows:
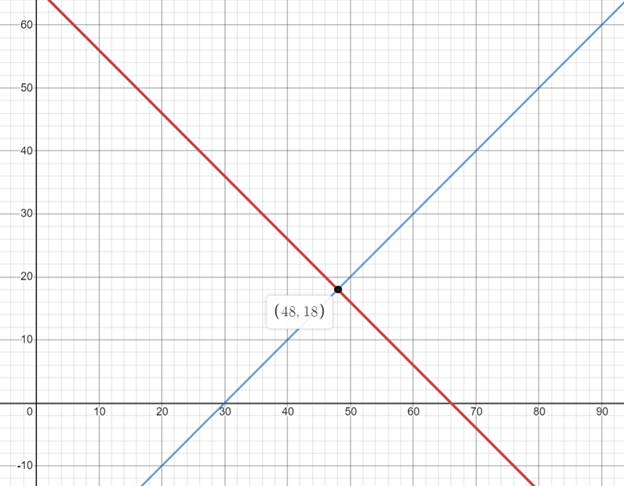
Interpretation:
From the above graph, the point of intersection of x and y co-ordinates is the same as the solutions found algebraically.
Conclusion:
Therefore, the solutions of the equations are verified graphically.
Chapter 6 Solutions
Algebra 1
Ch. 6.1 - Prob. 1ACYPCh. 6.1 - Prob. 1BCYPCh. 6.1 - Prob. 2ACYPCh. 6.1 - Prob. 2BCYPCh. 6.1 - Prob. 3CYPCh. 6.1 - Prob. 1CYUCh. 6.1 - Prob. 2CYUCh. 6.1 - Prob. 3CYUCh. 6.1 - Prob. 4CYUCh. 6.1 - Prob. 5CYU
Ch. 6.1 - Prob. 6CYUCh. 6.1 - Prob. 7CYUCh. 6.1 - Prob. 8CYUCh. 6.1 - Prob. 9CYUCh. 6.1 - Prob. 10PPSCh. 6.1 - Prob. 11PPSCh. 6.1 - Prob. 12PPSCh. 6.1 - Prob. 13PPSCh. 6.1 - Prob. 14PPSCh. 6.1 - Prob. 15PPSCh. 6.1 - Prob. 16PPSCh. 6.1 - Prob. 17PPSCh. 6.1 - Prob. 18PPSCh. 6.1 - Prob. 19PPSCh. 6.1 - Prob. 20PPSCh. 6.1 - Prob. 21PPSCh. 6.1 - Prob. 22PPSCh. 6.1 - Prob. 23PPSCh. 6.1 - Prob. 24PPSCh. 6.1 - Prob. 25PPSCh. 6.1 - Prob. 26PPSCh. 6.1 - Prob. 27PPSCh. 6.1 - Prob. 28PPSCh. 6.1 - Prob. 29PPSCh. 6.1 - Prob. 30PPSCh. 6.1 - Prob. 31PPSCh. 6.1 - Prob. 32PPSCh. 6.1 - Prob. 33PPSCh. 6.1 - Prob. 34PPSCh. 6.1 - Prob. 35PPSCh. 6.1 - Prob. 36PPSCh. 6.1 - Prob. 37PPSCh. 6.1 - Prob. 38PPSCh. 6.1 - Prob. 39PPSCh. 6.1 - Prob. 40PPSCh. 6.1 - Prob. 41PPSCh. 6.1 - Prob. 42PPSCh. 6.1 - Prob. 43PPSCh. 6.1 - Prob. 44PPSCh. 6.1 - Prob. 45PPSCh. 6.1 - Prob. 46PPSCh. 6.1 - Prob. 47HPCh. 6.1 - Prob. 48HPCh. 6.1 - Prob. 49HPCh. 6.1 - Prob. 50HPCh. 6.1 - Prob. 51HPCh. 6.1 - Prob. 52HPCh. 6.1 - Prob. 53STPCh. 6.1 - Prob. 54STPCh. 6.1 - Prob. 55STPCh. 6.1 - Prob. 56STPCh. 6.1 - Prob. 57SRCh. 6.1 - Prob. 58SRCh. 6.1 - Prob. 59SRCh. 6.1 - Prob. 60SRCh. 6.1 - Prob. 61SRCh. 6.1 - Prob. 62SRCh. 6.1 - Prob. 63SRCh. 6.1 - Prob. 64SRCh. 6.1 - Prob. 65SRCh. 6.1 - Prob. 66SRCh. 6.1 - Prob. 67SRCh. 6.1 - Prob. 68SRCh. 6.1 - Prob. 69SCh. 6.1 - Prob. 70SCh. 6.1 - Prob. 71SCh. 6.1 - Prob. 72SCh. 6.1 - Prob. 73SCh. 6.1 - Prob. 74SCh. 6.1 - Prob. 75SCh. 6.1 - Prob. 76SCh. 6.2 - Prob. 1ACYPCh. 6.2 - Prob. 1BCYPCh. 6.2 - Prob. 2ACYPCh. 6.2 - Prob. 2BCYPCh. 6.2 - Prob. 3ACYPCh. 6.2 - Prob. 3BCYPCh. 6.2 - Prob. 4CYPCh. 6.2 - Prob. 1CYUCh. 6.2 - Prob. 2CYUCh. 6.2 - Prob. 3CYUCh. 6.2 - Prob. 4CYUCh. 6.2 - Prob. 5CYUCh. 6.2 - Prob. 6CYUCh. 6.2 - Prob. 7CYUCh. 6.2 - Prob. 8PPSCh. 6.2 - Prob. 9PPSCh. 6.2 - Prob. 10PPSCh. 6.2 - Prob. 11PPSCh. 6.2 - Prob. 12PPSCh. 6.2 - Prob. 13PPSCh. 6.2 - Prob. 14PPSCh. 6.2 - Prob. 15PPSCh. 6.2 - Prob. 16PPSCh. 6.2 - Prob. 17PPSCh. 6.2 - Prob. 18PPSCh. 6.2 - Prob. 19PPSCh. 6.2 - Prob. 20PPSCh. 6.2 - Prob. 21PPSCh. 6.2 - Prob. 22PPSCh. 6.2 - Prob. 23PPSCh. 6.2 - Prob. 24PPSCh. 6.2 - Prob. 25PPSCh. 6.2 - Prob. 26PPSCh. 6.2 - Prob. 27HPCh. 6.2 - Prob. 28HPCh. 6.2 - Prob. 29HPCh. 6.2 - Prob. 30HPCh. 6.2 - Prob. 31HPCh. 6.2 - Prob. 32STPCh. 6.2 - Prob. 33STPCh. 6.2 - Prob. 34STPCh. 6.2 - Prob. 35STPCh. 6.2 - Prob. 36SRCh. 6.2 - Prob. 37SRCh. 6.2 - Prob. 38SRCh. 6.2 - Prob. 39SRCh. 6.2 - Prob. 40SRCh. 6.2 - Prob. 41SRCh. 6.2 - Prob. 42SRCh. 6.2 - Prob. 43SRCh. 6.2 - Prob. 44SRCh. 6.2 - Prob. 45SRCh. 6.2 - Prob. 46SRCh. 6.2 - Prob. 47SCh. 6.2 - Prob. 48SCh. 6.2 - Prob. 49SCh. 6.2 - Prob. 50SCh. 6.3 - Prob. 1ACYPCh. 6.3 - Prob. 1BCYPCh. 6.3 - Prob. 2CYPCh. 6.3 - Prob. 3CYPCh. 6.3 - Prob. 4CYPCh. 6.3 - Prob. 1CYUCh. 6.3 - Prob. 2CYUCh. 6.3 - Prob. 3CYUCh. 6.3 - Prob. 4CYUCh. 6.3 - Prob. 5CYUCh. 6.3 - Prob. 6CYUCh. 6.3 - Prob. 7PPSCh. 6.3 - Prob. 8PPSCh. 6.3 - Prob. 9PPSCh. 6.3 - Prob. 10PPSCh. 6.3 - Prob. 11PPSCh. 6.3 - Prob. 12PPSCh. 6.3 - Prob. 13PPSCh. 6.3 - Prob. 14PPSCh. 6.3 - Prob. 15PPSCh. 6.3 - Prob. 16PPSCh. 6.3 - Prob. 17PPSCh. 6.3 - Prob. 18PPSCh. 6.3 - Prob. 19PPSCh. 6.3 - Prob. 20PPSCh. 6.3 - Prob. 21PPSCh. 6.3 - Prob. 22PPSCh. 6.3 - Prob. 23PPSCh. 6.3 - Prob. 24PPSCh. 6.3 - Prob. 25PPSCh. 6.3 - Prob. 26PPSCh. 6.3 - Prob. 27PPSCh. 6.3 - Prob. 28PPSCh. 6.3 - Prob. 29PPSCh. 6.3 - Prob. 30PPSCh. 6.3 - Prob. 31PPSCh. 6.3 - Prob. 32PPSCh. 6.3 - Prob. 33PPSCh. 6.3 - Prob. 34HPCh. 6.3 - Prob. 35HPCh. 6.3 - Prob. 36HPCh. 6.3 - Prob. 37HPCh. 6.3 - Prob. 38HPCh. 6.3 - Prob. 39HPCh. 6.3 - Prob. 40STPCh. 6.3 - Prob. 41STPCh. 6.3 - Prob. 42STPCh. 6.3 - Prob. 43STPCh. 6.3 - Prob. 44SRCh. 6.3 - Prob. 45SRCh. 6.3 - Prob. 46SRCh. 6.3 - Prob. 47SRCh. 6.3 - Prob. 48SRCh. 6.3 - Prob. 49SRCh. 6.3 - Prob. 50SRCh. 6.3 - Prob. 51SRCh. 6.3 - Prob. 52SRCh. 6.3 - Prob. 53SRCh. 6.3 - Prob. 54SRCh. 6.3 - Prob. 55SRCh. 6.3 - Prob. 56SCh. 6.3 - Prob. 57SCh. 6.3 - Prob. 58SCh. 6.3 - Prob. 59SCh. 6.4 - Prob. 1ACYPCh. 6.4 - Prob. 1BCYPCh. 6.4 - Prob. 2ACYPCh. 6.4 - Prob. 2BCYPCh. 6.4 - Prob. 3CYPCh. 6.4 - Prob. 1CYUCh. 6.4 - Prob. 2CYUCh. 6.4 - Prob. 3CYUCh. 6.4 - Prob. 4CYUCh. 6.4 - Prob. 5CYUCh. 6.4 - Prob. 6CYUCh. 6.4 - Prob. 7PPSCh. 6.4 - Prob. 8PPSCh. 6.4 - Prob. 9PPSCh. 6.4 - Prob. 10PPSCh. 6.4 - Prob. 11PPSCh. 6.4 - Prob. 12PPSCh. 6.4 - Prob. 13PPSCh. 6.4 - Prob. 14PPSCh. 6.4 - Prob. 15PPSCh. 6.4 - Prob. 16PPSCh. 6.4 - Prob. 17PPSCh. 6.4 - Prob. 18PPSCh. 6.4 - Prob. 19PPSCh. 6.4 - Prob. 20PPSCh. 6.4 - Prob. 21PPSCh. 6.4 - Prob. 22PPSCh. 6.4 - Prob. 23PPSCh. 6.4 - Prob. 24PPSCh. 6.4 - Prob. 25PPSCh. 6.4 - Prob. 26PPSCh. 6.4 - Prob. 27PPSCh. 6.4 - Prob. 28PPSCh. 6.4 - Prob. 29HPCh. 6.4 - Prob. 30HPCh. 6.4 - Prob. 31HPCh. 6.4 - Prob. 32HPCh. 6.4 - Prob. 33HPCh. 6.4 - Prob. 34STPCh. 6.4 - Prob. 35STPCh. 6.4 - Prob. 36STPCh. 6.4 - Prob. 37STPCh. 6.4 - Prob. 38SRCh. 6.4 - Prob. 39SRCh. 6.4 - Prob. 40SRCh. 6.4 - Prob. 41SRCh. 6.4 - Prob. 42SRCh. 6.4 - Prob. 43SRCh. 6.4 - Prob. 44SRCh. 6.4 - Prob. 45SRCh. 6.4 - Prob. 46SRCh. 6.4 - Prob. 47SRCh. 6.4 - Prob. 48SRCh. 6.4 - Prob. 49SCh. 6.4 - Prob. 50SCh. 6.4 - Prob. 51SCh. 6.4 - Prob. 52SCh. 6.4 - Prob. 53SCh. 6.4 - Prob. 54SCh. 6.5 - Prob. 1ACYPCh. 6.5 - Prob. 1BCYPCh. 6.5 - Prob. 1CCYPCh. 6.5 - Prob. 1DCYPCh. 6.5 - Prob. 2CYPCh. 6.5 - Prob. 1CYUCh. 6.5 - Prob. 2CYUCh. 6.5 - Prob. 3CYUCh. 6.5 - Prob. 4CYUCh. 6.5 - Prob. 5CYUCh. 6.5 - Prob. 6PPSCh. 6.5 - Prob. 7PPSCh. 6.5 - Prob. 8PPSCh. 6.5 - Prob. 9PPSCh. 6.5 - Prob. 10PPSCh. 6.5 - Prob. 11PPSCh. 6.5 - Prob. 12PPSCh. 6.5 - Prob. 13PPSCh. 6.5 - Prob. 14PPSCh. 6.5 - Prob. 15PPSCh. 6.5 - Prob. 16PPSCh. 6.5 - Prob. 17PPSCh. 6.5 - Prob. 18PPSCh. 6.5 - Prob. 19PPSCh. 6.5 - Prob. 20PPSCh. 6.5 - Prob. 21HPCh. 6.5 - Prob. 22HPCh. 6.5 - Prob. 23HPCh. 6.5 - Prob. 24HPCh. 6.5 - Prob. 25HPCh. 6.5 - Prob. 26HPCh. 6.5 - Prob. 27STPCh. 6.5 - Prob. 28STPCh. 6.5 - Prob. 29STPCh. 6.5 - Prob. 30STPCh. 6.5 - Prob. 31SRCh. 6.5 - Prob. 32SRCh. 6.5 - Prob. 33SRCh. 6.5 - Prob. 34SRCh. 6.5 - Prob. 35SRCh. 6.5 - Prob. 36SRCh. 6.5 - Prob. 37SRCh. 6.5 - Prob. 38SRCh. 6.5 - Prob. 39SCh. 6.5 - Prob. 40SCh. 6.5 - Prob. 41SCh. 6.5 - Prob. 42SCh. 6.5 - Prob. 43SCh. 6.5 - Prob. 44SCh. 6.6 - Prob. 1ACYPCh. 6.6 - Prob. 1BCYPCh. 6.6 - Prob. 3ACYPCh. 6.6 - Prob. 3BCYPCh. 6.6 - Prob. 4ACYPCh. 6.6 - Prob. 4BCYPCh. 6.6 - Prob. 5ACYPCh. 6.6 - Prob. 5BCYPCh. 6.6 - Prob. 1CYUCh. 6.6 - Prob. 2CYUCh. 6.6 - Prob. 3CYUCh. 6.6 - Prob. 4CYUCh. 6.6 - Prob. 5CYUCh. 6.6 - Prob. 6CYUCh. 6.6 - Prob. 7CYUCh. 6.6 - Prob. 8CYUCh. 6.6 - Prob. 9CYUCh. 6.6 - Prob. 10PPSCh. 6.6 - Prob. 11PPSCh. 6.6 - Prob. 12PPSCh. 6.6 - Prob. 13PPSCh. 6.6 - Prob. 14PPSCh. 6.6 - Prob. 15PPSCh. 6.6 - Prob. 16PPSCh. 6.6 - Prob. 17PPSCh. 6.6 - Prob. 18PPSCh. 6.6 - Prob. 19PPSCh. 6.6 - Prob. 20PPSCh. 6.6 - Prob. 21PPSCh. 6.6 - Prob. 22PPSCh. 6.6 - Prob. 23PPSCh. 6.6 - Prob. 24PPSCh. 6.6 - Prob. 26PPSCh. 6.6 - Prob. 27PPSCh. 6.6 - Prob. 28PPSCh. 6.6 - Prob. 29PPSCh. 6.6 - Prob. 30PPSCh. 6.6 - Prob. 31PPSCh. 6.6 - Prob. 32PPSCh. 6.6 - Prob. 33HPCh. 6.6 - Prob. 34HPCh. 6.6 - Prob. 35HPCh. 6.6 - Prob. 36HPCh. 6.6 - Prob. 37HPCh. 6.6 - Prob. 38HPCh. 6.6 - Prob. 39STPCh. 6.6 - Prob. 40STPCh. 6.6 - Prob. 41STPCh. 6.6 - Prob. 43SRCh. 6.6 - Prob. 44SRCh. 6.6 - Prob. 45SRCh. 6.6 - Prob. 46SRCh. 6.6 - Prob. 47SRCh. 6.6 - Prob. 48SRCh. 6.6 - Prob. 49SRCh. 6.6 - Prob. 50SRCh. 6.6 - Prob. 51SRCh. 6.6 - Prob. 52SCh. 6.6 - Prob. 53SCh. 6.6 - Prob. 54SCh. 6.6 - Prob. 55SCh. 6.6 - Prob. 56SCh. 6.6 - Prob. 57SCh. 6.6 - Prob. 2CYPCh. 6.6 - Prob. 25PPSCh. 6.6 - Prob. 42STPCh. 6.7 - Prob. 1ACYPCh. 6.7 - Prob. 1BCYPCh. 6.7 - Prob. 2ACYPCh. 6.7 - Prob. 2BCYPCh. 6.7 - Prob. 1CYUCh. 6.7 - Prob. 2CYUCh. 6.7 - Prob. 3CYUCh. 6.7 - Prob. 4CYUCh. 6.7 - Prob. 5CYUCh. 6.7 - Prob. 6CYUCh. 6.7 - Prob. 7CYUCh. 6.7 - Prob. 8CYUCh. 6.7 - Prob. 9CYUCh. 6.7 - Prob. 10CYUCh. 6.7 - Prob. 11CYUCh. 6.7 - Prob. 12PPSCh. 6.7 - Prob. 13PPSCh. 6.7 - Prob. 14PPSCh. 6.7 - Prob. 15PPSCh. 6.7 - Prob. 16PPSCh. 6.7 - Prob. 17PPSCh. 6.7 - Prob. 18PPSCh. 6.7 - Prob. 19PPSCh. 6.7 - Prob. 20PPSCh. 6.7 - Prob. 21PPSCh. 6.7 - Prob. 22PPSCh. 6.7 - Prob. 23PPSCh. 6.7 - Prob. 24PPSCh. 6.7 - Prob. 25PPSCh. 6.7 - Prob. 26PPSCh. 6.7 - Prob. 27PPSCh. 6.7 - Prob. 28PPSCh. 6.7 - Prob. 29PPSCh. 6.7 - Prob. 30PPSCh. 6.7 - Prob. 31PPSCh. 6.7 - Prob. 32PPSCh. 6.7 - Prob. 33PPSCh. 6.7 - Prob. 34PPSCh. 6.7 - Prob. 35PPSCh. 6.7 - Prob. 36PPSCh. 6.7 - Prob. 37PPSCh. 6.7 - Prob. 38PPSCh. 6.7 - Prob. 39PPSCh. 6.7 - Prob. 40PPSCh. 6.7 - Prob. 41PPSCh. 6.7 - Prob. 42PPSCh. 6.7 - Prob. 43PPSCh. 6.7 - Prob. 44PPSCh. 6.7 - Prob. 45PPSCh. 6.7 - Prob. 47HPCh. 6.7 - Prob. 49HPCh. 6.7 - Prob. 50HPCh. 6.7 - Prob. 52STPCh. 6.7 - Prob. 53STPCh. 6.7 - Prob. 54STPCh. 6.7 - Prob. 55STPCh. 6.7 - Prob. 56SRCh. 6.7 - Prob. 57SRCh. 6.7 - Prob. 58SRCh. 6.7 - Prob. 59SRCh. 6.7 - Prob. 60SRCh. 6.7 - Prob. 62SRCh. 6.7 - Prob. 63SRCh. 6.7 - Prob. 64SRCh. 6.7 - Prob. 65SRCh. 6.7 - Prob. 66SRCh. 6.7 - Prob. 67SRCh. 6.7 - Prob. 68SCh. 6.7 - Prob. 69SCh. 6.7 - Prob. 70SCh. 6.7 - Prob. 71SCh. 6.7 - Prob. 72SCh. 6.7 - Prob. 73SCh. 6.7 - Prob. 3CYPCh. 6.7 - Prob. 48HPCh. 6.7 - Prob. 51HPCh. 6.7 - Prob. 61SRCh. 6.8 - Prob. 3BCYPCh. 6.8 - Prob. 3CYUCh. 6.8 - Prob. 7CYUCh. 6.8 - Prob. 8CYUCh. 6.8 - Prob. 9CYUCh. 6.8 - Prob. 10PPSCh. 6.8 - Prob. 11PPSCh. 6.8 - Prob. 12PPSCh. 6.8 - Prob. 13PPSCh. 6.8 - Prob. 14PPSCh. 6.8 - Prob. 15PPSCh. 6.8 - Prob. 16PPSCh. 6.8 - Prob. 17PPSCh. 6.8 - Prob. 18PPSCh. 6.8 - Prob. 19PPSCh. 6.8 - Prob. 20PPSCh. 6.8 - Prob. 21PPSCh. 6.8 - Prob. 22PPSCh. 6.8 - Prob. 23PPSCh. 6.8 - Prob. 24PPSCh. 6.8 - Prob. 25PPSCh. 6.8 - Prob. 26PPSCh. 6.8 - Prob. 27PPSCh. 6.8 - Prob. 28PPSCh. 6.8 - Prob. 29PPSCh. 6.8 - Prob. 30PPSCh. 6.8 - Prob. 31PPSCh. 6.8 - Prob. 32PPSCh. 6.8 - Prob. 33PPSCh. 6.8 - Prob. 34PPSCh. 6.8 - Prob. 35PPSCh. 6.8 - Prob. 36PPSCh. 6.8 - Prob. 37PPSCh. 6.8 - Prob. 38HPCh. 6.8 - Prob. 39HPCh. 6.8 - Prob. 40HPCh. 6.8 - Prob. 41HPCh. 6.8 - Prob. 42HPCh. 6.8 - Prob. 43HPCh. 6.8 - Prob. 44STPCh. 6.8 - Prob. 45STPCh. 6.8 - Prob. 46STPCh. 6.8 - Prob. 47STPCh. 6.8 - Prob. 48SRCh. 6.8 - Prob. 49SRCh. 6.8 - Prob. 50SRCh. 6.8 - Prob. 51SRCh. 6.8 - Prob. 52SRCh. 6.8 - Prob. 53SRCh. 6.8 - Prob. 54SRCh. 6.8 - Prob. 55SRCh. 6.8 - Prob. 56SRCh. 6.8 - Prob. 57SRCh. 6.8 - Prob. 58SRCh. 6.8 - Prob. 59SRCh. 6.8 - Prob. 60SRCh. 6.8 - Prob. 61SRCh. 6.8 - Prob. 62SRCh. 6.8 - Prob. 63SRCh. 6.8 - Prob. 64SCh. 6.8 - Prob. 65SCh. 6.8 - Prob. 66SCh. 6.8 - Prob. 1ACYPCh. 6.8 - Prob. 1BCYPCh. 6.8 - Prob. 1CCYPCh. 6.8 - Prob. 1DCYPCh. 6.8 - Prob. 2ACYPCh. 6.8 - Prob. 2BCYPCh. 6.8 - Prob. 1CYUCh. 6.8 - Prob. 2CYUCh. 6.8 - Prob. 4CYUCh. 6.8 - Prob. 5CYUCh. 6.8 - Prob. 6CYUCh. 6.8 - Prob. 3ACYPCh. 6.8 - Prob. 3CCYPCh. 6.8 - Prob. 3DCYPCh. 6 - Prob. 1QCCh. 6 - Prob. 2QCCh. 6 - Prob. 3QCCh. 6 - Prob. 4QCCh. 6 - Prob. 5QCCh. 6 - Prob. 6QCCh. 6 - Prob. 7QCCh. 6 - Prob. 8QCCh. 6 - Prob. 9QCCh. 6 - Prob. 10QCCh. 6 - Prob. 11QCCh. 6 - Prob. 12QCCh. 6 - Prob. 13QCCh. 6 - Prob. 1MCQCh. 6 - Prob. 2MCQCh. 6 - Prob. 3MCQCh. 6 - Prob. 4MCQCh. 6 - Prob. 5MCQCh. 6 - Prob. 6MCQCh. 6 - Prob. 7MCQCh. 6 - Prob. 8MCQCh. 6 - Prob. 9MCQCh. 6 - Prob. 10MCQCh. 6 - Prob. 11MCQCh. 6 - Prob. 12MCQCh. 6 - Prob. 13MCQCh. 6 - Prob. 14MCQCh. 6 - Prob. 15MCQCh. 6 - Prob. 16MCQCh. 6 - Prob. 17MCQCh. 6 - Prob. 18MCQCh. 6 - Prob. 19MCQCh. 6 - Prob. 20MCQCh. 6 - Prob. 1SGRCh. 6 - Prob. 2SGRCh. 6 - Prob. 3SGRCh. 6 - Prob. 4SGRCh. 6 - Prob. 5SGRCh. 6 - Prob. 6SGRCh. 6 - Prob. 7SGRCh. 6 - Prob. 8SGRCh. 6 - Prob. 9SGRCh. 6 - Prob. 10SGRCh. 6 - Prob. 11SGRCh. 6 - Prob. 12SGRCh. 6 - Prob. 13SGRCh. 6 - Prob. 14SGRCh. 6 - Prob. 15SGRCh. 6 - Prob. 16SGRCh. 6 - Prob. 17SGRCh. 6 - Prob. 18SGRCh. 6 - Prob. 19SGRCh. 6 - Prob. 20SGRCh. 6 - Prob. 21SGRCh. 6 - Prob. 22SGRCh. 6 - Prob. 23SGRCh. 6 - Prob. 24SGRCh. 6 - Prob. 25SGRCh. 6 - Prob. 26SGRCh. 6 - Prob. 27SGRCh. 6 - Prob. 28SGRCh. 6 - Prob. 29SGRCh. 6 - Prob. 30SGRCh. 6 - Prob. 31SGRCh. 6 - Prob. 32SGRCh. 6 - Prob. 33SGRCh. 6 - Prob. 34SGRCh. 6 - Prob. 35SGRCh. 6 - Prob. 36SGRCh. 6 - Prob. 37SGRCh. 6 - Prob. 38SGRCh. 6 - Prob. 39SGRCh. 6 - Prob. 40SGRCh. 6 - Prob. 41SGRCh. 6 - Prob. 42SGRCh. 6 - Prob. 43SGRCh. 6 - Prob. 44SGRCh. 6 - Prob. 45SGRCh. 6 - Prob. 46SGRCh. 6 - Prob. 47SGRCh. 6 - Prob. 48SGRCh. 6 - Prob. 49SGRCh. 6 - Prob. 50SGRCh. 6 - Prob. 51SGRCh. 6 - Prob. 52SGRCh. 6 - Prob. 53SGRCh. 6 - Prob. 54SGRCh. 6 - Prob. 56SGRCh. 6 - Prob. 57SGRCh. 6 - Prob. 58SGRCh. 6 - Prob. 59SGRCh. 6 - Prob. 60SGRCh. 6 - Prob. 61SGRCh. 6 - Prob. 62SGRCh. 6 - Prob. 63SGRCh. 6 - Prob. 64SGRCh. 6 - Prob. 65SGRCh. 6 - Prob. 66SGRCh. 6 - Prob. 67SGRCh. 6 - Prob. 68SGRCh. 6 - Prob. 69SGRCh. 6 - Prob. 70SGRCh. 6 - Prob. 9PTCh. 6 - Prob. 12PTCh. 6 - Prob. 14PTCh. 6 - Prob. 1STPCh. 6 - Prob. 2STPCh. 6 - Prob. 3STPCh. 6 - Prob. 4STPCh. 6 - Prob. 5STPCh. 6 - Prob. 6STPCh. 6 - Prob. 7STPCh. 6 - Prob. 9STPCh. 6 - Prob. 10STPCh. 6 - Prob. 11STPCh. 6 - Prob. 12STPCh. 6 - Prob. 13STPCh. 6 - Prob. 14STPCh. 6 - Prob. 16STPCh. 6 - Prob. 17STPCh. 6 - Prob. 18STPCh. 6 - Prob. 1PTCh. 6 - Prob. 2PTCh. 6 - Prob. 3PTCh. 6 - Prob. 4PTCh. 6 - Prob. 5PTCh. 6 - Prob. 6PTCh. 6 - Prob. 8PTCh. 6 - Prob. 10PTCh. 6 - Prob. 11PTCh. 6 - Prob. 13PTCh. 6 - Prob. 15PTCh. 6 - Prob. 16PTCh. 6 - Prob. 17PTCh. 6 - Prob. 18PTCh. 6 - Prob. 19PTCh. 6 - Prob. 20PTCh. 6 - Prob. 21PTCh. 6 - Prob. 22PTCh. 6 - Prob. 23PTCh. 6 - Prob. 24PTCh. 6 - Prob. 25PTCh. 6 - Prob. 55SGRCh. 6 - Prob. 71SGRCh. 6 - Prob. 7PTCh. 6 - Prob. 8STPCh. 6 - Prob. 15STP
Additional Math Textbook Solutions
Find more solutions based on key concepts
In Exercises 9-12, assume that 50 births are randomly selected. Use subjective judgment to describe the given n...
Elementary Statistics (13th Edition)
Explain the meaning of the term “statistically significant difference” in statistics terminology.
Intro Stats, Books a la Carte Edition (5th Edition)
Two dice are thrown. Let E be the event that the sum of the dice is odd, let F be the event that at least one o...
A First Course in Probability (10th Edition)
TRY IT YOURSELF 1
Find the mean of the points scored by the 51 winning teams listed on page 39.
Elementary Statistics: Picturing the World (7th Edition)
Fill in each blank so that the resulting statement is true. Any set of ordered pairs is called a/an ____.The se...
Algebra and Trigonometry (6th Edition)
Find the point-slope form of the line passing through the given points. Use the first point as (x1, .y1). Plot ...
College Algebra with Modeling & Visualization (5th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- A professor gives two types of quizzes, objective and recall. He plans to give at least 15 quizzes this quarter. The student preparation time for an objective quiz is 15 minutes and for a recall quiz 30 minutes. The professor would like a student to spend at least 5 hours total (300 minutes) preparing for these quizzes. It takes the professor 1 minute to grade an objective quiz, and 1.5 minutes to grade a recall type quiz. How many of each type of quiz should the professor give in order to minimize his grading time (why still meeting the other requirements outlined)?arrow_forwardTable 15-21 shows the relative frequencies of the scores of a group of students on a philosophy quiz.Table 15-21 Score45678 Relative frequency7%11%19%24%39%arrow_forwardInstructions: Answer each question showing all work. 1. Out of 30 animals at a veterinarian clinic, 8 cats and 4 dogs have been vaccinated. 6 cats and 12 dogs are not yet vaccinated. Create a two-way frequency table to represent the data. 2. Convert the table from number 1 into a two-way relative frequency table. Instructions: Based on the tables created in questions 1 and 2 above, answer questions 3-7. 3. What percentage of cats from the total animals are vaccinated? 4. What is the relative frequency of dogs from the total animals that are not yet vaccinated? 5. What is the conditional frequency of cats that have not been vaccinated? 6. What is the marginal frequency of the total number of animals vaccinated? 7. What is the joint frequency of the cats that are vaccinated?arrow_forward
- The the high 3000arrow_forwardHow long will it take you to double your money if you invest it at a rate of 8% compounded annually?arrow_forwardOne hundred dollars is invested at 7.2% interest compounded annually. Determine how much the investment is worth after: a. I year b. 5 years c. 10 years d. 20 years e. Use your answers to parts (a)-(d) to estimate the doubling time for the investment.arrow_forward
- 6) A farmer has 60 acres on which to plant oats or corn. Each acre of oats requires 100 lbs of fertilizer and 1 hour of labor. Each acre of corn requires 50 lbs of fertilizer and 2 hours of labor. The farmer has 5000 lbs of fertilizer and 100 hours available for labor. If the profit is $60 from each acre of oats and $100 from each acre of corn, what planting combination will produce the greatest total profit? a) Fill in the following chart to help organize the information given in the problem: Oats Labor Fertilizer Land Profit b) Write down the question of interest. Corn Available c) Define variables to answer the question of interest. Call these x and y. d) Write the objective function to answer the question of interest. e) List any constraints given in the problem.arrow_forwardI need help with number 5.arrow_forward3) Use the following system of linear inequalities graphed below to answer the questions. a) Use the graph to write the symbolic form of the system of linear inequalities. b) Is (-4,2) a solution to the system? Explain. 5 -7 -5 -3 -2 0 2 3 4 $ 6 -2 -6 -7arrow_forward
- ) Graph the feasible region subject to the following constraints. x + y ≤ 6 y ≤ 2x x ≥ 0, y ≥ 0 P + xarrow_forwardSolve the following system of equations: 50x+20y=1800 10x+3y=300arrow_forward> > > we are hiring Salesforce Admin Location: Remote Key Responsibilities: Administer Salesforce Sales & Revenue Cloud (CPQ & Billing) Configure workflows, validation rules & dashboards Automate processes using Flows & Process Builder Collaborate with Sales, Finance & Marketing teams Manage user roles & security Apply: Hr@forcecraver.comarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
UG/ linear equation in linear algebra; Author: The Gate Academy;https://www.youtube.com/watch?v=aN5ezoOXX5A;License: Standard YouTube License, CC-BY
System of Linear Equations-I; Author: IIT Roorkee July 2018;https://www.youtube.com/watch?v=HOXWRNuH3BE;License: Standard YouTube License, CC-BY