Thinking Mathematically Plus MyLab Math -- Access Card Package (7th Edition) (What's New in Service Math)
7th Edition
ISBN: 9780134708300
Author: Robert F. Blitzer
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 6.3, Problem 20E
How will you spend your average life expectancy of 78 years? The bar group shows the average number of years you will devote to each of your most time-consuming activities. Exercises 19-20 are based on the data displayed by the graph.
How you will Spend Your Average Life Expectancy of 78 Years
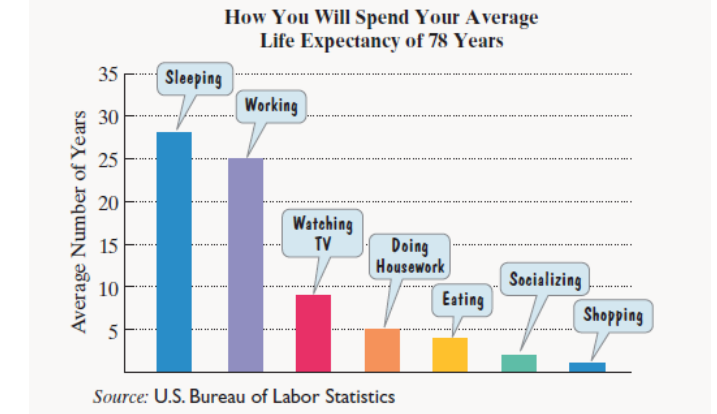
According to the U.S. Bureau of Labor Statistics, you will devote 32 years to sleeping and eating. The number of sleeping will exceed the number of years eating by 24. Over your lifetime, how many years will you spend on each of these activities?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Please calculate the shaded area
An investigator analyzed the leading digits from 797 checks issued by seven suspect companies. The frequencies were found to be 0, 19, 2, 50, 361, 309, 10, 22, and 24, and those digits correspond to the
leading digits of 1, 2, 3, 4, 5, 6, 7, 8, and 9, respectively. If the observed frequencies are substantially different from the frequencies expected with Benford's law shown below, the check amounts appear to result
from fraud. Use a 0.10 significance level to test for goodness-of-fit with Benford's law. Does it appear that the checks are the result of fraud?
Leading Digit
Actual Frequency
Benford's Law: Distribution of Leading Digits
1
2
3
4
5
6
7
8
9
0
19
2
50
361
309
10
22
24
30.1%
17.6%
12.5%
9.7%
7.9%
6.7%
5.8%
5.1%
4.6%
Determine the null and alternative hypotheses.
Ho The leading digits are from a population that conforms to Benford's law.
H₁: At least one leading digit has a frequency that does not conform to Benford's law.
Calculate the test statistic, x².
x²
=
(Round to three…
3. Solve the Heat Equation with Initial and Boundary Conditions
Turn to page 71 for the heat equation problem. Solve the partial differential equation using
Fourier series or another suitable method, given the initial and boundary conditions.
Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view?
usp=sharing]
Provide all derivations and intermediate steps.
Chapter 6 Solutions
Thinking Mathematically Plus MyLab Math -- Access Card Package (7th Edition) (What's New in Service Math)
Ch. 6.1 - CHECK POINT 1 Evaluate .
Ch. 6.1 - CHECK POINT 2 Evaluate x 2 + 4 x − 7 for x = −...Ch. 6.1 - CHECK POINT 3 Evaluate − 3 x 2 + 4 x y − y 3 for...Ch. 6.1 - CHECK POINT 4 The mathematic model M = − 120 x 2 +...Ch. 6.1 - Prob. 5CPCh. 6.1 - CHECK POINT 6 Simplify: 7 ( 4 x 2 + 3 x ) + 2 ( 5...Ch. 6.1 - Prob. 7CPCh. 6.1 - Fill in each blank so that the resulting statement...Ch. 6.1 - Fill in each blank so that the resulting statement...Ch. 6.1 - Fill in each blank so that the resulting statement...
Ch. 6.1 - Prob. 4CVCCh. 6.1 - Prob. 5CVCCh. 6.1 - Prob. 6CVCCh. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - Prob. 3ECh. 6.1 - Prob. 4ECh. 6.1 - Prob. 5ECh. 6.1 - Prob. 6ECh. 6.1 - Prob. 7ECh. 6.1 - Prob. 8ECh. 6.1 - Prob. 9ECh. 6.1 - Prob. 10ECh. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - Prob. 12ECh. 6.1 - Prob. 13ECh. 6.1 - Prob. 14ECh. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - Prob. 16ECh. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - In Exercises 1-34, evaluate the algebraic...Ch. 6.1 - Prob. 24ECh. 6.1 - Prob. 25ECh. 6.1 - Prob. 26ECh. 6.1 - Prob. 27ECh. 6.1 - Prob. 28ECh. 6.1 - Prob. 29ECh. 6.1 - Prob. 30ECh. 6.1 - Prob. 31ECh. 6.1 - Prob. 32ECh. 6.1 - Prob. 33ECh. 6.1 - Prob. 34ECh. 6.1 - The formula C = 5 9 ( F − 32 ) expresses the...Ch. 6.1 - Prob. 36ECh. 6.1 - Prob. 37ECh. 6.1 - Prob. 38ECh. 6.1 - In Exercises 39-40, name the property used to go...Ch. 6.1 - Prob. 40ECh. 6.1 - In Exercises 41-62, simplify each algebraic...Ch. 6.1 - Prob. 42ECh. 6.1 - Prob. 43ECh. 6.1 - Prob. 44ECh. 6.1 - In Exercises 41-62, simplify each algebraic...Ch. 6.1 - In Exercises 41-62, simplify each algebraic...Ch. 6.1 - Prob. 47ECh. 6.1 - Prob. 48ECh. 6.1 - Prob. 49ECh. 6.1 - In Exercises 41-62, simplify each algebraic...Ch. 6.1 - Prob. 51ECh. 6.1 - Prob. 52ECh. 6.1 - Prob. 53ECh. 6.1 - In Exercises 41-62, simplify each algebraic...Ch. 6.1 - In Exercises 41-62, simplify each algebraic...Ch. 6.1 - Prob. 56ECh. 6.1 - Prob. 57ECh. 6.1 - In Exercises 41-62, simplify each algebraic...Ch. 6.1 - Prob. 59ECh. 6.1 - Prob. 60ECh. 6.1 - Prob. 61ECh. 6.1 - Prob. 62ECh. 6.1 - Prob. 63ECh. 6.1 - Prob. 64ECh. 6.1 - Prob. 65ECh. 6.1 - Prob. 66ECh. 6.1 - 67. If you exercise goal is to improve...Ch. 6.1 - Prob. 68ECh. 6.1 - The bar graph shows the estimated number of...Ch. 6.1 - Prob. 70ECh. 6.1 - Prob. 71ECh. 6.1 - Source: MonsterCollege TM The mathematical model p...Ch. 6.1 - Read the Blitzer Bonus on page 346. Use the...Ch. 6.1 - Prob. 74ECh. 6.1 - Prob. 75ECh. 6.1 - Prob. 76ECh. 6.1 - Prob. 77ECh. 6.1 - Prob. 78ECh. 6.1 - Prob. 79ECh. 6.1 - Prob. 80ECh. 6.1 - Prob. 81ECh. 6.1 - Prob. 82ECh. 6.1 - Prob. 83ECh. 6.1 - Prob. 84ECh. 6.1 - Prob. 85ECh. 6.1 - Prob. 86ECh. 6.1 - Prob. 87ECh. 6.1 - Prob. 88ECh. 6.1 - Prob. 89ECh. 6.1 - Prob. 90ECh. 6.1 - Prob. 91ECh. 6.1 - Prob. 92ECh. 6.1 - A business that manufactures small alarm clocks...Ch. 6.2 - CHECK POINT 1 Solve and check:
Ch. 6.2 - CHECK POINT 2 Solve and check: 6 ( x − 3 ) − 10 x...Ch. 6.2 - CHECK POINT 3 Solve the equation: 2 x + 9 = 8 x −...Ch. 6.2 - CHECK POINT 4 Solve and check: 4 ( 2 x + 1 ) = 29...Ch. 6.2 - CHECK POINT 5 Solve and check: 2 x 3 = 7 − x 2 .Ch. 6.2 - CHECK POINT 6 Use the model the low-humor group...Ch. 6.2 - $$ CHECK POINT 7 Solve each proportion and check:...Ch. 6.2 - CHECK POINT 8 The property tax on a house with an...Ch. 6.2 - CHECK POINT 9 Wildlife biologists catch, tag and...Ch. 6.2 - CHECK POINT 10 Solve: 3 x + 7 = 3 ( x + 1 ) .Ch. 6.2 - CHECK POINT 11 Solve: .
Ch. 6.2 - 1. An equation in the form such as is called...Ch. 6.2 - 2. Two or more equations that have the same...Ch. 6.2 - 3. The addition property of equality states that...Ch. 6.2 - 4. The multiplication property of equality states...Ch. 6.2 - 5. The first step in solving is to ____.
Ch. 6.2 - 6. The algebraic expression can be ____, whereas...Ch. 6.2 - The equation x 4 = 2 + x 3 can be cleared of...Ch. 6.2 - A statement that two ratios are equal is called...Ch. 6.2 - The cross-products principle states that if a b =...Ch. 6.2 - In solving an equation, if you eliminate the...Ch. 6.2 - 11. In solving an equation with variable x, if you...Ch. 6.2 - In Exercises 12-15, determine whether each...Ch. 6.2 - In Exercises 12-15, determine whether each...Ch. 6.2 - In Exercises 12-15, determine whether each...Ch. 6.2 - In Exercises 12-15, determine whether each...Ch. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 2ECh. 6.2 - Prob. 3ECh. 6.2 - Prob. 4ECh. 6.2 - Prob. 5ECh. 6.2 - Prob. 6ECh. 6.2 - Prob. 7ECh. 6.2 - Prob. 8ECh. 6.2 - Prob. 9ECh. 6.2 - Prob. 10ECh. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 12ECh. 6.2 - Prob. 13ECh. 6.2 - Prob. 14ECh. 6.2 - Prob. 15ECh. 6.2 - Prob. 16ECh. 6.2 - Prob. 17ECh. 6.2 - Prob. 18ECh. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 20ECh. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - Prob. 22ECh. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 24ECh. 6.2 - Prob. 25ECh. 6.2 - Prob. 26ECh. 6.2 - Prob. 27ECh. 6.2 - Prob. 28ECh. 6.2 - Prob. 29ECh. 6.2 - Prob. 30ECh. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - Prob. 32ECh. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 34ECh. 6.2 - Prob. 35ECh. 6.2 - Prob. 36ECh. 6.2 - Prob. 37ECh. 6.2 - Prob. 38ECh. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 40ECh. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 42ECh. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - Prob. 46ECh. 6.2 - In Exercises 1-58, solve and check each...Ch. 6.2 - Prob. 48ECh. 6.2 - Prob. 49ECh. 6.2 - Prob. 50ECh. 6.2 - Prob. 51ECh. 6.2 - Prob. 52ECh. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - Prob. 56ECh. 6.2 - Prob. 57ECh. 6.2 - In Exercises 1-58, solve and check each equation....Ch. 6.2 - In Exercises 59-72, solve each proportion and...Ch. 6.2 - Prob. 60ECh. 6.2 - In Exercises 59-72, solve each proportion and...Ch. 6.2 - Prob. 62ECh. 6.2 - In Exercises 59-72, solve each proportion and...Ch. 6.2 - Prob. 64ECh. 6.2 - Prob. 65ECh. 6.2 - Prob. 66ECh. 6.2 - In Exercises 59-72, solve each proportion and...Ch. 6.2 - Prob. 68ECh. 6.2 - Prob. 69ECh. 6.2 - Prob. 70ECh. 6.2 - In Exercises 59-72, solve each proportion and...Ch. 6.2 - In Exercises 59-72, solve each proportion and...Ch. 6.2 - Prob. 73ECh. 6.2 - Prob. 74ECh. 6.2 - Prob. 75ECh. 6.2 - Prob. 76ECh. 6.2 - Prob. 77ECh. 6.2 - Prob. 78ECh. 6.2 - Prob. 79ECh. 6.2 - Prob. 80ECh. 6.2 - Prob. 81ECh. 6.2 - Prob. 82ECh. 6.2 - Prob. 83ECh. 6.2 - Prob. 84ECh. 6.2 - In Exercises 73-92, solve each equation. Use set...Ch. 6.2 - In Exercises 73-92, solve each equation. Use set...Ch. 6.2 - In Exercises 73-92, solve each equation. Use set...Ch. 6.2 - Prob. 88ECh. 6.2 - In Exercises 73-92, solve each equation. Use set...Ch. 6.2 - Prob. 90ECh. 6.2 - Prob. 91ECh. 6.2 - In Exercises 73-92, solve each equation. Use set...Ch. 6.2 - Prob. 93ECh. 6.2 - Prob. 94ECh. 6.2 - Prob. 95ECh. 6.2 - 96. Evaluate for x satisfying and y satisfying...Ch. 6.2 - Prob. 97ECh. 6.2 - In Exercises 97- 104, solve each equation.
98.
Ch. 6.2 - Prob. 99ECh. 6.2 - Prob. 100ECh. 6.2 - Prob. 101ECh. 6.2 - Prob. 102ECh. 6.2 - Prob. 103ECh. 6.2 - Prob. 104ECh. 6.2 - The mathematical model
describe a weight, W in...Ch. 6.2 - The mathematical model W 2 − 3 H = 53 describe a...Ch. 6.2 - Grade Inflation. The bar graph shows the...Ch. 6.2 - Grade Inflation. The bar graph shows the...Ch. 6.2 - 109. The volume of blood in a person’s body is...Ch. 6.2 - Prob. 110ECh. 6.2 - 111. An alligator’s tail length is proportional to...Ch. 6.2 - 112. An object’s weight on the moon is...Ch. 6.2 - Prob. 113ECh. 6.2 - 114. To estimate the number of base in a lake,...Ch. 6.2 - Prob. 115ECh. 6.2 - State the addition property of equality and give...Ch. 6.2 - Prob. 117ECh. 6.2 - Prob. 118ECh. 6.2 - Prob. 119ECh. 6.2 - Prob. 120ECh. 6.2 - Prob. 121ECh. 6.2 - Prob. 122ECh. 6.2 - Prob. 123ECh. 6.2 - Prob. 124ECh. 6.2 - Prob. 125ECh. 6.2 - Prob. 126ECh. 6.2 - Prob. 127ECh. 6.2 - Prob. 128ECh. 6.2 - 129. Write three equations whose solution set is...Ch. 6.2 - 130. If x represent a number, write an English...Ch. 6.2 - 131. A woman’s height, h, is related to the length...Ch. 6.3 - CHECK POINT 1 The average yearly salary of a woman...Ch. 6.3 - Prob. 2CPCh. 6.3 - CHECK POINT 3 The toll to a bridge costs $5....Ch. 6.3 - CHECK POINT 4 After a 30% price reducing, you...Ch. 6.3 - Prob. 5CPCh. 6.3 - Prob. 6CPCh. 6.3 - 1. According to the U.S. Office of Management and...Ch. 6.3 - In 2000, 31% of U.S. adults viewed a college...Ch. 6.3 - Prob. 3CVCCh. 6.3 - Prob. 4CVCCh. 6.3 - Prob. 5CVCCh. 6.3 - Prob. 6CVCCh. 6.3 - Use the five-step strategy for solving word...Ch. 6.3 - Use the five- step strategy for solving word...Ch. 6.3 - Prob. 3ECh. 6.3 - Prob. 4ECh. 6.3 - Use the five- step strategy for solving word...Ch. 6.3 - Use the five- step strategy for solving word...Ch. 6.3 - Use the five- step strategy for solving word...Ch. 6.3 - Prob. 8ECh. 6.3 - Prob. 9ECh. 6.3 - Prob. 10ECh. 6.3 - In Exercises 11-18, write each English phrase as...Ch. 6.3 - Prob. 12ECh. 6.3 - In Exercises 11-18, write each English phrase as...Ch. 6.3 - In Exercises 11-18, write each English phrase as...Ch. 6.3 - Prob. 15ECh. 6.3 - Prob. 16ECh. 6.3 - Prob. 17ECh. 6.3 - In Exercises 11-18, write each English phrase as...Ch. 6.3 - How will you spend your average life expectancy of...Ch. 6.3 - How will you spend your average life expectancy of...Ch. 6.3 - The bar graph shows average yearly earnings in the...Ch. 6.3 - The bar graph shows average yearly earnings in the...Ch. 6.3 - Prob. 23ECh. 6.3 - Prob. 24ECh. 6.3 - On average, every minute of every day, 158 babies...Ch. 6.3 - On average, every minute of every day, 158 babies...Ch. 6.3 - Prob. 27ECh. 6.3 - Prob. 28ECh. 6.3 - Prob. 29ECh. 6.3 - You need to rent a rug cleaner. Company A will...Ch. 6.3 - Prob. 31ECh. 6.3 - Prob. 32ECh. 6.3 - Prob. 33ECh. 6.3 - Prob. 34ECh. 6.3 - Prob. 35ECh. 6.3 - Prob. 36ECh. 6.3 - Prob. 37ECh. 6.3 - Prob. 38ECh. 6.3 - Prob. 39ECh. 6.3 - Prob. 40ECh. 6.3 - Prob. 41ECh. 6.3 - Prob. 42ECh. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - Prob. 44ECh. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - In Exercises 43-60, solve each formula for the...Ch. 6.3 - Prob. 58ECh. 6.3 - Prob. 59ECh. 6.3 - Prob. 60ECh. 6.3 - Prob. 61ECh. 6.3 - Prob. 62ECh. 6.3 - Prob. 63ECh. 6.3 - Prob. 64ECh. 6.3 - Make Sense? In Exercises 65-68, determine whether...Ch. 6.3 - Make Sense? In Exercises 65-68, determine whether...Ch. 6.3 - Prob. 67ECh. 6.3 - Prob. 68ECh. 6.3 - Prob. 69ECh. 6.3 - Prob. 70ECh. 6.3 - Prob. 71ECh. 6.3 - Prob. 72ECh. 6.3 - A thief steals a number of rare plants from a...Ch. 6.3 - Prob. 74ECh. 6.3 - Prob. 75ECh. 6.3 - One of the best ways to learn how to solve a word...Ch. 6.4 - $$ CHECK POINT I Graph each set: a. { x | x < 4 }...Ch. 6.4 - Prob. 2CPCh. 6.4 - Prob. 3CPCh. 6.4 - Prob. 4CPCh. 6.4 - Prob. 5CPCh. 6.4 - Prob. 6CPCh. 6.4 - Prob. 7CPCh. 6.4 - 1. On a number line, an open dot indicates that a...Ch. 6.4 - 2. If an inequality’s solution set consists of...Ch. 6.4 - 3. If an inequality’s solution set consists of all...Ch. 6.4 - Prob. 4CVCCh. 6.4 - Prob. 5CVCCh. 6.4 - Prob. 6CVCCh. 6.4 - Prob. 7CVCCh. 6.4 - In Exercises 5-8, determine whether each statement...Ch. 6.4 - In Exercises 1-12, graph each set of real numbers...Ch. 6.4 - Prob. 2ECh. 6.4 - Prob. 3ECh. 6.4 - In Exercises 1-12, graph each set of real numbers...Ch. 6.4 - Prob. 5ECh. 6.4 - Prob. 6ECh. 6.4 - Prob. 7ECh. 6.4 - Prob. 8ECh. 6.4 - Prob. 9ECh. 6.4 - Prob. 10ECh. 6.4 - Prob. 11ECh. 6.4 - Prob. 12ECh. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - Prob. 30ECh. 6.4 - Prob. 31ECh. 6.4 - Prob. 32ECh. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - Prob. 34ECh. 6.4 - Prob. 35ECh. 6.4 - Prob. 36ECh. 6.4 - Prob. 37ECh. 6.4 - Prob. 38ECh. 6.4 - Prob. 39ECh. 6.4 - Prob. 40ECh. 6.4 - Prob. 41ECh. 6.4 - Prob. 42ECh. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - Prob. 52ECh. 6.4 - Prob. 53ECh. 6.4 - Prob. 54ECh. 6.4 - Prob. 55ECh. 6.4 - Prob. 56ECh. 6.4 - Prob. 57ECh. 6.4 - Prob. 58ECh. 6.4 - Prob. 59ECh. 6.4 - Prob. 60ECh. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - In Exercises 13-66, solve each inequality and...Ch. 6.4 - Prob. 64ECh. 6.4 - Prob. 65ECh. 6.4 - Prob. 66ECh. 6.4 - Prob. 67ECh. 6.4 - Prob. 68ECh. 6.4 - Prob. 69ECh. 6.4 - Prob. 70ECh. 6.4 - In Exercises 71-76, use set-builder notation to...Ch. 6.4 - Prob. 72ECh. 6.4 - Prob. 73ECh. 6.4 - Prob. 74ECh. 6.4 - Prob. 75ECh. 6.4 - Prob. 76ECh. 6.4 - Prob. 77ECh. 6.4 - Prob. 78ECh. 6.4 - The graphs show that the three components of love,...Ch. 6.4 - Prob. 80ECh. 6.4 - Prob. 81ECh. 6.4 - The graphs show that the three components of love,...Ch. 6.4 - Prob. 83ECh. 6.4 - Prob. 84ECh. 6.4 - models the percentage of U.S. households in which...Ch. 6.4 - Prob. 86ECh. 6.4 - Prob. 87ECh. 6.4 - Prob. 88ECh. 6.4 - Prob. 89ECh. 6.4 - Prob. 90ECh. 6.4 - Prob. 91ECh. 6.4 - Prob. 92ECh. 6.4 - Prob. 93ECh. 6.4 - Prob. 94ECh. 6.4 - Prob. 95ECh. 6.4 - Prob. 96ECh. 6.4 - Prob. 97ECh. 6.4 - Prob. 98ECh. 6.4 - Prob. 99ECh. 6.4 - Prob. 100ECh. 6.4 - Prob. 101ECh. 6.4 - Prob. 102ECh. 6.4 - Prob. 103ECh. 6.4 - Prob. 104ECh. 6.5 - CHECK POINT 1 Multiple:
Ch. 6.5 - CHECK POINT 2 Multiple: ( 7 x + 5 ) ( 4 x − 3 )Ch. 6.5 - Prob. 3CPCh. 6.5 - Prob. 4CPCh. 6.5 - CHECK POINT 5 Factor: 5 x 2 − 14 x + 8Ch. 6.5 - Prob. 6CPCh. 6.5 - Prob. 7CPCh. 6.5 - Prob. 8CPCh. 6.5 - Prob. 9CPCh. 6.5 - Prob. 10CPCh. 6.5 - Prob. 11CPCh. 6.5 - Prob. 12CPCh. 6.5 - Prob. 1CVCCh. 6.5 - Prob. 2CVCCh. 6.5 - Prob. 3CVCCh. 6.5 - Prob. 4CVCCh. 6.5 - Prob. 5CVCCh. 6.5 - Prob. 6CVCCh. 6.5 - Prob. 7CVCCh. 6.5 - Prob. 8CVCCh. 6.5 - Prob. 9CVCCh. 6.5 - Prob. 10CVCCh. 6.5 - The zero-product principle states that if A B = 0...Ch. 6.5 - Prob. 12CVCCh. 6.5 - Prob. 13CVCCh. 6.5 - Prob. 14CVCCh. 6.5 - Prob. 15CVCCh. 6.5 - Prob. 16CVCCh. 6.5 - Prob. 17CVCCh. 6.5 - Prob. 18CVCCh. 6.5 - Prob. 1ECh. 6.5 - Prob. 2ECh. 6.5 - Prob. 3ECh. 6.5 - Prob. 4ECh. 6.5 - Prob. 5ECh. 6.5 - Prob. 6ECh. 6.5 - Prob. 7ECh. 6.5 - Prob. 8ECh. 6.5 - Prob. 9ECh. 6.5 - Prob. 10ECh. 6.5 - Factor the trinomials in Exercises 9-32, or state...Ch. 6.5 - Prob. 12ECh. 6.5 - Factor the trinomials in Exercises 9-32, or state...Ch. 6.5 - Prob. 14ECh. 6.5 - Prob. 15ECh. 6.5 - Prob. 16ECh. 6.5 - Prob. 17ECh. 6.5 - Prob. 18ECh. 6.5 - Prob. 19ECh. 6.5 - Prob. 20ECh. 6.5 - Factor the trinomials in Exercises 9-32, or state...Ch. 6.5 - Prob. 22ECh. 6.5 - Factor the trinomials in Exercises 9-32, or state...Ch. 6.5 - Prob. 24ECh. 6.5 - Prob. 25ECh. 6.5 - Prob. 26ECh. 6.5 - Prob. 27ECh. 6.5 - Prob. 28ECh. 6.5 - Factor the trinomials in Exercises 9-32, or state...Ch. 6.5 - Prob. 30ECh. 6.5 - Prob. 31ECh. 6.5 - Prob. 32ECh. 6.5 - In Exercises 33-36, solve each equation using the...Ch. 6.5 - Prob. 34ECh. 6.5 - In Exercises 33-36, solve each equation using the...Ch. 6.5 - Prob. 36ECh. 6.5 - Solve the quadratic equations in Exercises 37-52,...Ch. 6.5 - Prob. 38ECh. 6.5 - Prob. 39ECh. 6.5 - Prob. 40ECh. 6.5 - Prob. 41ECh. 6.5 - Prob. 42ECh. 6.5 - Prob. 43ECh. 6.5 - Prob. 44ECh. 6.5 - Prob. 45ECh. 6.5 - Prob. 46ECh. 6.5 - Prob. 47ECh. 6.5 - Prob. 48ECh. 6.5 - Prob. 49ECh. 6.5 - Prob. 50ECh. 6.5 - Prob. 51ECh. 6.5 - Prob. 52ECh. 6.5 - Prob. 53ECh. 6.5 - Prob. 54ECh. 6.5 - Solve the equations in Exercises 53-72 using the...Ch. 6.5 - Prob. 56ECh. 6.5 - Prob. 57ECh. 6.5 - Prob. 58ECh. 6.5 - Prob. 59ECh. 6.5 - Prob. 60ECh. 6.5 - Prob. 61ECh. 6.5 - Prob. 62ECh. 6.5 - Prob. 63ECh. 6.5 - Prob. 64ECh. 6.5 - Prob. 65ECh. 6.5 - Prob. 66ECh. 6.5 - Prob. 67ECh. 6.5 - Prob. 68ECh. 6.5 - Prob. 69ECh. 6.5 - Prob. 70ECh. 6.5 - Prob. 71ECh. 6.5 - Prob. 72ECh. 6.5 - Prob. 73ECh. 6.5 - Prob. 74ECh. 6.5 - Prob. 75ECh. 6.5 - Prob. 76ECh. 6.5 - Prob. 77ECh. 6.5 - Prob. 78ECh. 6.5 - Prob. 79ECh. 6.5 - Prob. 80ECh. 6.5 - Prob. 81ECh. 6.5 - Prob. 82ECh. 6.5 - Prob. 83ECh. 6.5 - Prob. 84ECh. 6.5 - Prob. 85ECh. 6.5 - Prob. 86ECh. 6.5 - Prob. 87ECh. 6.5 - Prob. 88ECh. 6.5 - 89. Explain how to factor .
Ch. 6.5 - Prob. 90ECh. 6.5 - Prob. 91ECh. 6.5 - Prob. 92ECh. 6.5 - Prob. 93ECh. 6.5 - Prob. 94ECh. 6.5 - Prob. 95ECh. 6.5 - Prob. 96ECh. 6.5 - The radicand of the quadratic formula, b 2 − 4 a c...Ch. 6.5 - Prob. 98ECh. 6.5 - In Exercises 98-99, find all positive integers b...Ch. 6.5 - Prob. 100ECh. 6.5 - Prob. 101ECh. 6 - In Exercises 1-3, evaluate the algebraic...Ch. 6 - In Exercises 1-3, evaluate the algebraic...Ch. 6 - Prob. 3RECh. 6 - Prob. 4RECh. 6 - In Exercises 5-7, simplify each algebraic...Ch. 6 - Prob. 6RECh. 6 - Prob. 7RECh. 6 - Prob. 8RECh. 6 - Prob. 9RECh. 6 - Prob. 10RECh. 6 - Prob. 11RECh. 6 - Prob. 12RECh. 6 - Prob. 13RECh. 6 - Prob. 14RECh. 6 - Prob. 15RECh. 6 - In Exercises 15-18, solve each proportion.
16.
Ch. 6 - Prob. 17RECh. 6 - Prob. 18RECh. 6 - Prob. 19RECh. 6 - 20. To determine the number of trout in a lake, a...Ch. 6 - 21. The line graph showy he cost of inflation....Ch. 6 - Prob. 22RECh. 6 - Prob. 23RECh. 6 - 24. You are choosing between two cellphone plans....Ch. 6 - Prob. 25RECh. 6 - Prob. 26RECh. 6 - Prob. 27RECh. 6 - Prob. 28RECh. 6 - Prob. 29RECh. 6 - Prob. 30RECh. 6 - Prob. 31RECh. 6 - Prob. 32RECh. 6 - Prob. 33RECh. 6 - Prob. 34RECh. 6 - Prob. 35RECh. 6 - Prob. 36RECh. 6 - In Exercises 31-37, solve each inequality and...Ch. 6 - Prob. 38RECh. 6 - Prob. 39RECh. 6 - Prob. 40RECh. 6 - Prob. 41RECh. 6 - Prob. 42RECh. 6 - Prob. 43RECh. 6 - Prob. 44RECh. 6 - Prob. 45RECh. 6 - Prob. 46RECh. 6 - Prob. 47RECh. 6 - Prob. 48RECh. 6 - Prob. 49RECh. 6 - Prob. 50RECh. 6 - Prob. 51RECh. 6 - Prob. 52RECh. 6 - Prob. 53RECh. 6 - Prob. 54RECh. 6 - Prob. 55RECh. 6 - 1. Evaluate when .
Ch. 6 - Prob. 2TCh. 6 - Prob. 3TCh. 6 - Prob. 4TCh. 6 - Prob. 5TCh. 6 - Prob. 6TCh. 6 - Prob. 7TCh. 6 - Prob. 8TCh. 6 - Prob. 9TCh. 6 - Prob. 10TCh. 6 - Prob. 11TCh. 6 - Prob. 12TCh. 6 - Prob. 13TCh. 6 - Prob. 14TCh. 6 - Prob. 15TCh. 6 - Prob. 16TCh. 6 - Prob. 17TCh. 6 - Prob. 18TCh. 6 - Prob. 19TCh. 6 - Prob. 20TCh. 6 - Prob. 21TCh. 6 - Prob. 22TCh. 6 - Prob. 23TCh. 6 - Prob. 24TCh. 6 - Prob. 25TCh. 6 - Prob. 26T
Additional Math Textbook Solutions
Find more solutions based on key concepts
For each hour of class time, how many hours outside of class are recommended for studying and doing homework?
Elementary Algebra For College Students (10th Edition)
NOTE: Write your answers using interval notation when appropriate.
CHECKING ANALYTIC SKILLS Fill in each blank ...
Graphical Approach To College Algebra
(a) Make a stem-and-leaf plot for these 24 observations on the number of customers who used a down-town CitiBan...
APPLIED STAT.IN BUS.+ECONOMICS
Let F be a continuous distribution function. If U is uniformly distributed on (0,1), find the distribution func...
A First Course in Probability (10th Edition)
Fill in each blank so that the resulting statement is true.
1. The degree of the polynomial function is _____....
Algebra and Trigonometry (6th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Name: Tay Jones Level Two Date: Algebra 3 Unit 3: Functions and Equations Practice Assessment Class: #7-OneNote 1. The function f(x) = x² is transformed in the following functions. List the vertex for each function, circle whether the function opens up or down, and why. All three parts must be correct to receive Level 2 points. You can receive points for a, b, and c. a) g(x) = -2(x+5)² Vertex: Opens Up Opens Down Why? ais negative -2 Vertex: b) g(x) = (x + 2)² - 3 c) g(x) = -4(x + 2)² + 2 Opens Up Opens Down Vertex: Opens Up Opens Down Why? 4 Ca is negative) Why? his positive 2. The graph of the function f(x) is shown below. Find the domain, range, and end behavior. Then list the values of x for which the function values are increasing and decreasing. f(x) Domain: End Behavior: As x → ∞o, f(x) -> -6 As x, f(x) -> Range: Where is it Increasing? (002] Where is it Decreasing? (1,00)arrow_forwardFor the distribution drawn here, identify the mean, median, and mode. Question content area bottom Part 1 A. Aequalsmode, Bequalsmedian, Cequalsmean B. Aequalsmode, Bequalsmean, Cequalsmedian C. Aequalsmedian, Bequalsmode, Cequalsmean D. Aequalsmean, Bequalsmode, Cequalsmedianarrow_forwardQ3: Define the linear functional J: H₁(2) R by ¡(v) = a(v, v) - L(v) Л Let u be the unique weak solution to a(u,v) = L(v) in H(2) and suppose that a(...) is a symmetric bilinear form on H(2) prove that 1- u is minimizer. 2- u is unique. 3- The minimizer J(u) can be rewritten under 1(u) = u Au-ub, algebraic form 1 2 Where A, b are repictively the stiffence matrix and the load vector Q4: A) Answer 1- show that the solution to -Au = f in A, u = 0 on a satisfies the stability Vullfll and show that ||V(u u)||||||2 - ||vu||2 2- Prove that Where lu-ul Chuz - !ull = a(u, u) = Vu. Vu dx + fu. uds B) Consider the bilinea forta Л a(u, v) = (Au, Av) (Vu, Vv + (Vu, v) + (u,v) Show that a(u, v) continues and V- elliptic on H(2)arrow_forward
- 2. Classify the Stability of Fixed Points in a Dynamical System The dynamical system problem is located on page 60 of the file. Identify the fixed points and classify their stability using linearization and eigenvalues. Link: [https://drive.google.com/file/d/1RQ2OZk-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Provide a detailed explanation of your analysis.arrow_forwardEvaluate the Z-Transform of the Sequence The Z-transform problem is provided on page 70. Compute the Z-transform of the given sequence and determine the region of convergence. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Show all steps and provide detailed reasoning.arrow_forward7. Apply Green's Theorem to Evaluate the Line Integral Check page 55 for the Green's theorem problem. Use Green's theorem to convert a line integral into a double integral and compute the result. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxp RyejKEMg1t2q15dbpVLCS/view? usp=sharing] Provide a detailed explanation and calculation.arrow_forward
- 8. Perform Singular Value Decomposition (SVD) on a Matrix The SVD problem can be found on page 66. Decompose the given matrix into its singular values, left singular vectors, and right singular vectors. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2ql5dbpVLCS/view? usp=sharing] Show the complete process and verify the decomposition.arrow_forward6. Diagonalize the Matrix and Verify the Result Check page 64 of the document for the matrix diagonalization problem. Find the eigenvalues and eigenvectors to diagonalize the matrix, then verify the result. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Present all calculations systematically.arrow_forward9. Analyze the Fourier Transform of a Discontinuous Function Refer to page 67 for the Fourier transform problem. Compute the Fourier transform of the given piecewise function and discuss its properties. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Present all steps in detail.arrow_forward
- 4. Determine the Taylor Series Expansion About a Point Refer to page 62 for the Taylor series problem. Find the Taylor series expansion of the function about the specified point and include the radius of convergence. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Explain the methodology and verify the series.arrow_forward10. Prove the Orthogonality of Eigenfunctions Go to page 68 of the document for the eigenfunction problem. Prove the orthogonality of the eigenfunctions of a given Sturm-Liouville problem. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Provide a rigorous proof, including necessary integrals and conditions.arrow_forwardShow what to do on the graph visually please!arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Elementary Algebra
Algebra
ISBN:9780998625713
Author:Lynn Marecek, MaryAnne Anthony-Smith
Publisher:OpenStax - Rice University
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
The Shape of Data: Distributions: Crash Course Statistics #7; Author: CrashCourse;https://www.youtube.com/watch?v=bPFNxD3Yg6U;License: Standard YouTube License, CC-BY
Shape, Center, and Spread - Module 20.2 (Part 1); Author: Mrmathblog;https://www.youtube.com/watch?v=COaid7O_Gag;License: Standard YouTube License, CC-BY
Shape, Center and Spread; Author: Emily Murdock;https://www.youtube.com/watch?v=_YyW0DSCzpM;License: Standard Youtube License