
Statics and Mechanics of Materials Plus Mastering Engineering with Pearson eText - Access Card Package (5th Edition)
5th Edition
ISBN: 9780134301006
Author: Russell C. Hibbeler
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 6.2, Problem 53P
Major floor loadings in a shop are caused by the weights of the objects shown. Each force acts through its respective center of gravity G. Locate the center of gravity
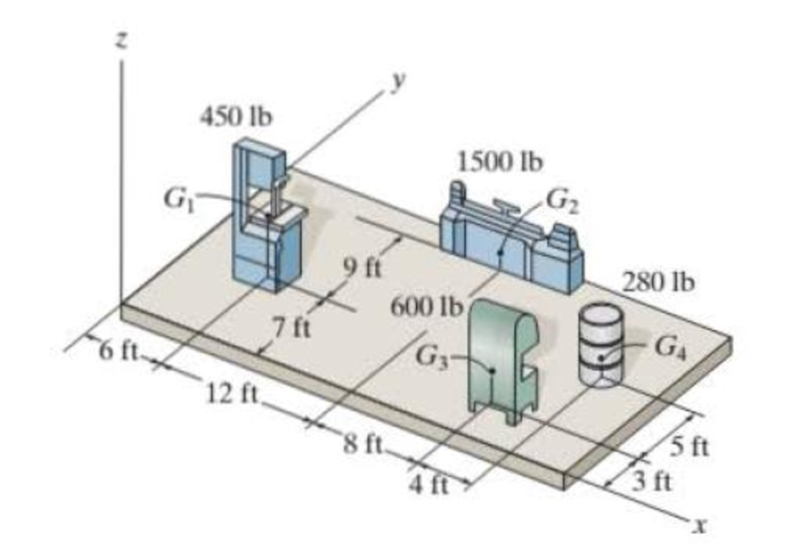
Prob. 6–53
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The heated rod from Problem 3 is subject to a volumetric heating
h(x) = h0
x
L in units of [Wm−3], as shown in the figure below. Under the
heat supply the temperature of the rod changes along x with the
temperature function T (x). The temperature T (x) is governed by the
d
following equations:
−
dx (q(x)) + h(x) = 0 PDE
q(x) =−k dT
dx Fourier’s law of heat conduction (4)
where q(x) is the heat flux through the rod and k is the (constant)
thermal conductivity. Both ends of the bar are in contact with a heat
reservoir at zero temperature.
Determine:
1. Appropriate BCs for this physical problem.
2. The temperature function T (x).
3. The heat flux function q(x).
Side Note: Please see that both ends of bar are in contact with a heat reservoir at zero temperature so the boundary condition at the right cannot be du/dx=0 because its not thermally insulated. Thank you
The elastic bar from Problem 1 spins with angular velocity ω about an axis, as shown in the figure below. The radial acceleration at a generic point x along the bar is a(x) = ω2x. Under this radial acceleration, the bar stretches along x with displacement function u(x). The displacement d u(x) is governed by the following equations: dx (σ(x)) + ρa(x) = 0 PDE σ(x) = E du dx Hooke’s law (2) where σ(x) is the axial stress in the rod, ρ is the mass density, and E is the (constant) Young’s modulus. The bar is pinned on the rotation axis at x = 0 and it is also pinned at x = L. Determine: 1. Appropriate BCs for this physical problem. 2. The displacement function u(x). 3. The stress function σ(x). SIDE QUESTION: I saw a tutor solve it before but I didn't understand why the tutor did not divide E under the second term (c1x) before finding u(x). The tutor only divided E under first term. please explain and thank you
calculate the total power required to go 80 mph in a VW Type 2 Samba Bus weighing 2310 lbs. with a Cd of 0.35 and a frontal area of 30ft^2. Consider the coefficient of rolling resistance to be 0.018. What is the increase in power required to go the same speed if the weight is increased by 2205 pounds (the rated carrying capacity of the vehicle). If the rated power for the vehicle is 49 bhp, will the van be able to reach 80 mph at full carrying capacity?
Chapter 6 Solutions
Statics and Mechanics of Materials Plus Mastering Engineering with Pearson eText - Access Card Package (5th Edition)
Ch. 6.1 - In each case, use the element shown and specify...Ch. 6.1 - Prob. 1FPCh. 6.1 - Determine the centroid (x,y) of the area. Prob....Ch. 6.1 - Determine the centroid y of the area. Prob. F63Ch. 6.1 - Locate the center of gravity x of the straight rod...Ch. 6.1 - Prob. 5FPCh. 6.1 - Locate the centroid z of the homogeneous solid...Ch. 6.1 - Locate the centroid x of the area. Prob. 61Ch. 6.1 - Locate the centroid of the area. Prob. 62Ch. 6.1 - Locate the centroid x of the area. Probs. 63/4
Ch. 6.1 - Locate the centroid y of the area. Probs. 63/4Ch. 6.1 - Locate the centroid x of the area. Probs. 65/6Ch. 6.1 - Locate the centroid y of the area. Probs. 65/6Ch. 6.1 - Prob. 7PCh. 6.1 - Prob. 8PCh. 6.1 - Locate the centroid x of the area. Solve the...Ch. 6.1 - Prob. 10PCh. 6.1 - Prob. 11PCh. 6.1 - Prob. 12PCh. 6.1 - Locate the centroid y of the area. Probs. 612/13Ch. 6.1 - Prob. 14PCh. 6.1 - Prob. 15PCh. 6.1 - Prob. 16PCh. 6.1 - Locate the centroid x of the area. Probs. 617/18Ch. 6.1 - Prob. 18PCh. 6.1 - Prob. 19PCh. 6.1 - Locate the centroid x of the area. Probs. 620/21Ch. 6.1 - Locate the centroid y of the area. Probs. 620/21Ch. 6.1 - Locate the centroid x of the area. Probs. 622/23Ch. 6.1 - Prob. 23PCh. 6.1 - Prob. 24PCh. 6.1 - Prob. 25PCh. 6.1 - Prob. 26PCh. 6.1 - Prob. 27PCh. 6.1 - The steel plate is 0.3 m thick and has a density...Ch. 6.1 - Prob. 29PCh. 6.1 - Prob. 30PCh. 6.1 - Prob. 31PCh. 6.1 - Prob. 32PCh. 6.1 - Prob. 33PCh. 6.1 - Locate the centroid z of the volume. Prob. 634Ch. 6.1 - Prob. 35PCh. 6.2 - Locate the centroid (x,y,z) of the wire bent in...Ch. 6.2 - Locate the centroid y of the beams cross-sectional...Ch. 6.2 - Locate the centroid y of the beams cross-sectional...Ch. 6.2 - Prob. 10FPCh. 6.2 - Prob. 11FPCh. 6.2 - Prob. 12FPCh. 6.2 - Locate the centroid (x,y) of the area. Prob. 636Ch. 6.2 - Locate the centroid y for the beams...Ch. 6.2 - Locate the centroid y of the beam having the...Ch. 6.2 - Locate the centroid (x,y) of the area. Prob. 639Ch. 6.2 - Locate the centroid y of the beams cross-sectional...Ch. 6.2 - Locate the centroid (x,y) of the area. Prob. 641Ch. 6.2 - Locate the centroid (x,y) of the area. Prob. 642Ch. 6.2 - Prob. 43PCh. 6.2 - Locate the centroid y of the cross-sectional area...Ch. 6.2 - Prob. 45PCh. 6.2 - Prob. 46PCh. 6.2 - Prob. 47PCh. 6.2 - Prob. 48PCh. 6.2 - Prob. 49PCh. 6.2 - Prob. 50PCh. 6.2 - Prob. 51PCh. 6.2 - Locate the center of gravity z of the assembly....Ch. 6.2 - Major floor loadings in a shop are caused by the...Ch. 6.2 - The assembly consists of a 20-in. wooden dowel rod...Ch. 6.2 - The composite plate is made from both steel (A)...Ch. 6.4 - Determine the moment of inertia of the area about...Ch. 6.4 - Prob. 14FPCh. 6.4 - Prob. 15FPCh. 6.4 - Determine the moment of inertia of the area about...Ch. 6.4 - Prob. 56PCh. 6.4 - Prob. 57PCh. 6.4 - Prob. 58PCh. 6.4 - Prob. 59PCh. 6.4 - Determine the moment of inertia for the area about...Ch. 6.4 - Determine the moment of inertia for the area about...Ch. 6.4 - Prob. 62PCh. 6.4 - Prob. 63PCh. 6.4 - Prob. 64PCh. 6.4 - Prob. 65PCh. 6.4 - Prob. 66PCh. 6.4 - Prob. 67PCh. 6.4 - Prob. 68PCh. 6.4 - Prob. 69PCh. 6.4 - Prob. 70PCh. 6.4 - Prob. 71PCh. 6.4 - Prob. 72PCh. 6.4 - Prob. 73PCh. 6.4 - Prob. 74PCh. 6.4 - Prob. 75PCh. 6.4 - Prob. 76PCh. 6.4 - Determine the moment of inertia for the area about...Ch. 6.4 - Determine the moment of inertia for the area about...Ch. 6.4 - Prob. 79PCh. 6.5 - Determine the moment of inertia of the...Ch. 6.5 - Determine the moment of inertia of the...Ch. 6.5 - Prob. 19FPCh. 6.5 - Determine the moment of inertia of the...Ch. 6.5 - Determine the moment of inertia of the composite...Ch. 6.5 - Determine the moment of inertia of the composite...Ch. 6.5 - Prob. 82PCh. 6.5 - Determine the location y of the centroid of the...Ch. 6.5 - Determine y, which locates the centroidal axis x...Ch. 6.5 - Prob. 85PCh. 6.5 - Prob. 86PCh. 6.5 - Determine the moment of inertia Ix of the area...Ch. 6.5 - Determine the moment of inertia Ix of the area...Ch. 6.5 - Determine the moment of inertia of the...Ch. 6.5 - Determine y, which locates the centroidal axis x...Ch. 6.5 - Determine the moment of inertia of the...Ch. 6.5 - Determine the moment of inertia of the...Ch. 6 - Locate the centroid x of the area.Ch. 6 - Locate the centroid y of the area.Ch. 6 - Locate the centroid of the rod.Ch. 6 - Prob. 4RPCh. 6 - Determine the moment of inertia for the area about...Ch. 6 - Prob. 6RPCh. 6 - Determine the area moment of inertia of the...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- A distillation column with a total of 13 actual stages (including a partial condenser) is used to perform a separation which requires 7 ideal stages. Calculate the overall column efficiency, and report your answer in %arrow_forward6. Consider a 10N step input to the mechanical system shown below, take M = 15kg, K = 135N/m, and b = 0.4 Ns/m. (a) Assume zero initial condition, calculate the (i) System pole (ii) System characterization, and (iii) The time domain response (b) Calculate the steady-state value of the system b [ www K 个 х M -F(+)arrow_forward2. Solve the following linear time invariant differential equations using Laplace transforms subject to different initial conditions (a) y-y=t for y(0) = 1 and y(0) = 1 (b) ÿ+4y+ 4y = u(t) for y(0) = 0 and y(0) = 1 (c) y-y-2y=0 for y(0) = 1 and y(0) = 0arrow_forward
- 3. For the mechanical systems shown below, the springs are undeflected when x₁ = x2 = x3 = 0 and the input is given as fa(t). Draw the free-body diagrams and write the modeling equations governing each of the systems. K₁ 000 K₂ 000 M₁ M2 -fa(t) B₂ B₁ (a) fa(t) M2 K₂ 000 B K₁ x1 000 M₁ (b)arrow_forwardThis question i m uploading second time . before you provide me incorrect answer. read the question carefully and solve accordily.arrow_forward1. Create a table comparing five different analogous variables for translational, rotational, electrical and fluid systems. Include the standard symbols for each variable in their respective systems.arrow_forward
- 2) Suppose that two unequal masses m₁ and m₂ are moving with initial velocities v₁ and v₂, respectively. The masses hit each other and have a coefficient of restitution e. After the impact, mass 1 and 2 head to their respective gaps at angles a and ẞ, respectively. Derive expressions for each of the angles in terms of the initial velocities and the coefficient of restitution. m1 m2 8 m1 m2 βarrow_forward4. Find the equivalent spring constant and equivalent viscous-friction coefficient for the systems shown below. @ B₁ B₂ H B3 (b)arrow_forward5. The cart shown below is inclined 30 degrees with respect to the horizontal. At t=0s, the cart is released from rest (i.e. with no initial velocity). If the air resistance is proportional to the velocity squared. Analytically determine the initial acceleration and final or steady-state velocity of the cart. Take M= 900 kg and b 44.145 Ns²/m². Mg -bx 2 отarrow_forward
- 9₁ A Insulated boundary Insulated boundary dx Let's begin with the strong form for a steady-state one-dimensional heat conduction problem, without convection. d dT + Q = dx dx According to Fourier's law of heat conduction, the heat flux q(x), is dT q(x)=-k dx. x Q is the internal heat source, which heat is generated per unit time per unit volume. q(x) and q(x + dx) are the heat flux conducted into the control volume at x and x + dx, respectively. k is thermal conductivity along the x direction, A is the cross-section area perpendicular to heat flux q(x). T is the temperature, and is the temperature gradient. dT dx 1. Derive the weak form using w(x) as the weight function. 2. Consider the following scenario: a 1D block is 3 m long (L = 3 m), with constant cross-section area A = 1 m². The left free surface of the block (x = 0) is maintained at a constant temperature of 200 °C, and the right surface (x = L = 3m) is insulated. Recall that Neumann boundary conditions are naturally satisfied…arrow_forward1 - Clearly identify the system and its mass and energy exchanges between each system and its surroundings by drawing a box to represent the system boundary, and showing the exchanges by input and output arrows. You may want to search and check the systems on the Internet in case you are not familiar with their operations. A pot with boiling water on a gas stove A domestic electric water heater A motor cycle driven on the roadfrom thermodynamics You just need to draw and put arrows on the first part a b and carrow_forward7. A distributed load w(x) = 4x1/3 acts on the beam AB shown in Figure 7, where x is measured in meters and w is in kN/m. The length of the beam is L = 4 m. Find the moment of the resultant force about the point B. w(x) per unit length L Figure 7 Barrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L

International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
moment of inertia; Author: NCERT OFFICIAL;https://www.youtube.com/watch?v=A4KhJYrt4-s;License: Standard YouTube License, CC-BY