
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
4th Edition
ISBN: 9781337687805
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Chapter 6.2, Problem 4E
To determine
Find the volume of the solid obtained by rotating the region bounded by the given curves.
Expert Solution & Answer
Answer to Problem 4E
The volume of the solid obtained by rotating the region bounded by the given curves is
Explanation of Solution
Given information: Given curves
Calculation:
The region is shown in the picture:
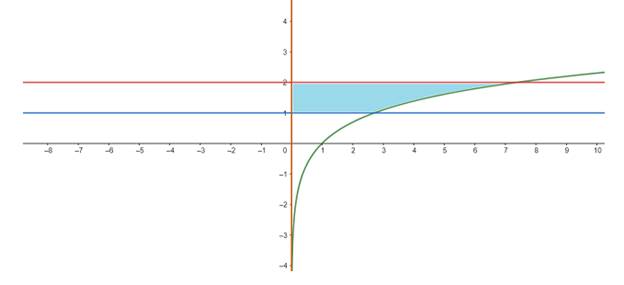
Rotate about
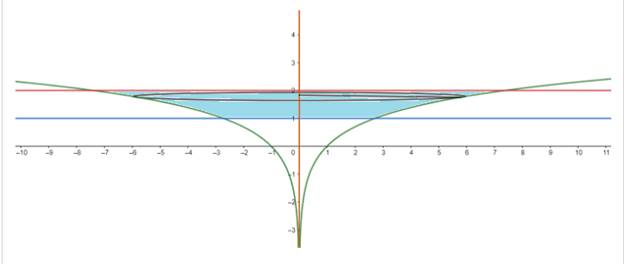
When we slice through the point
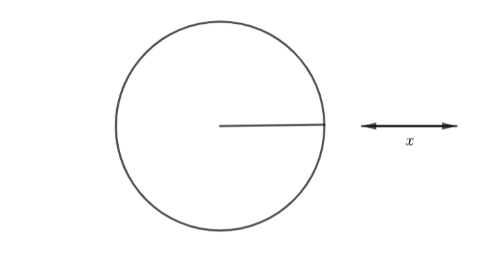

Thus, the volume of the solid obtained by rotating the region bounded by the given curves is
Chapter 6 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
Ch. 6.1 - Prob. 1ECh. 6.1 - Prob. 2ECh. 6.1 - Prob. 3ECh. 6.1 - Prob. 4ECh. 6.1 - Sketch the region enclosed by the given curves....Ch. 6.1 - Sketch the region enclosed by the given curves....Ch. 6.1 - Prob. 7ECh. 6.1 - Prob. 8ECh. 6.1 - Prob. 9ECh. 6.1 - Prob. 10E
Ch. 6.1 - Prob. 11ECh. 6.1 - Prob. 12ECh. 6.1 - Sketch the region enclosed by the given curves and...Ch. 6.1 - Sketch the region enclosed by the given curves and...Ch. 6.1 - Prob. 15ECh. 6.1 - Prob. 16ECh. 6.1 - Prob. 17ECh. 6.1 - Prob. 18ECh. 6.1 - Prob. 19ECh. 6.1 - Prob. 20ECh. 6.1 - Prob. 21ECh. 6.1 - Prob. 22ECh. 6.1 - Prob. 23ECh. 6.1 - Prob. 24ECh. 6.1 - Prob. 25ECh. 6.1 - Prob. 26ECh. 6.1 - The widths (in meters) of a kidney-shaped swimming...Ch. 6.1 - A cross-section of an airplane wing is shown....Ch. 6.1 - If the birth rate of a population is b(t) =...Ch. 6.1 - Prob. 30ECh. 6.1 - Prob. 31ECh. 6.1 - Prob. 32ECh. 6.1 - Prob. 33ECh. 6.1 - Prob. 34ECh. 6.1 - Prob. 35ECh. 6.1 - Prob. 36ECh. 6.1 - Prob. 37ECh. 6.1 - Prob. 38ECh. 6.1 - Prob. 39ECh. 6.1 - Prob. 40ECh. 6.1 - Prob. 41ECh. 6.1 - Prob. 42ECh. 6.1 - Prob. 43ECh. 6.1 - Prob. 44ECh. 6.1 - Prob. 45ECh. 6.2 - Prob. 1ECh. 6.2 - Prob. 2ECh. 6.2 - Prob. 3ECh. 6.2 - Prob. 4ECh. 6.2 - Prob. 5ECh. 6.2 - Prob. 6ECh. 6.2 - Prob. 7ECh. 6.2 - Prob. 8ECh. 6.2 - Prob. 9ECh. 6.2 - Prob. 10ECh. 6.2 - Prob. 11ECh. 6.2 - Prob. 12ECh. 6.2 - Prob. 13ECh. 6.2 - Prob. 14ECh. 6.2 - Prob. 15ECh. 6.2 - Prob. 16ECh. 6.2 - Prob. 17ECh. 6.2 - Prob. 18ECh. 6.2 - Prob. 19ECh. 6.2 - Prob. 20ECh. 6.2 - Prob. 21ECh. 6.2 - Prob. 22ECh. 6.2 - Prob. 23ECh. 6.2 - Prob. 24ECh. 6.2 - Prob. 25ECh. 6.2 - Prob. 26ECh. 6.2 - Prob. 27ECh. 6.2 - Prob. 28ECh. 6.2 - Prob. 29ECh. 6.2 - Prob. 31ECh. 6.2 - Find the volume of the described solid S. A...Ch. 6.2 - Prob. 33ECh. 6.2 - Prob. 34ECh. 6.2 - Prob. 35ECh. 6.2 - Prob. 36ECh. 6.2 - Prob. 37ECh. 6.2 - Prob. 38ECh. 6.2 - Prob. 39ECh. 6.2 - Prob. 40ECh. 6.2 - Prob. 41ECh. 6.2 - Prob. 42ECh. 6.2 - Prob. 43ECh. 6.2 - Prob. 44ECh. 6.2 - Prob. 45ECh. 6.2 - Prob. 46ECh. 6.2 - Prob. 47ECh. 6.2 - Prob. 48ECh. 6.2 - Prob. 49ECh. 6.2 - Prob. 50ECh. 6.2 - Prob. 51ECh. 6.2 - Prob. 52ECh. 6.2 - Prob. 53ECh. 6.2 - Prob. 54ECh. 6.3 - Let S be the solid obtained by rotating the region...Ch. 6.3 - Let S be the solid obtained by rotating the region...Ch. 6.3 - Prob. 3ECh. 6.3 - Prob. 4ECh. 6.3 - Prob. 5ECh. 6.3 - Prob. 6ECh. 6.3 - Prob. 7ECh. 6.3 - Prob. 8ECh. 6.3 - Prob. 9ECh. 6.3 - Prob. 10ECh. 6.3 - Prob. 11ECh. 6.3 - Prob. 12ECh. 6.3 - Prob. 13ECh. 6.3 - Prob. 14ECh. 6.3 - Prob. 15ECh. 6.3 - Prob. 16ECh. 6.3 - Prob. 17ECh. 6.3 - Prob. 18ECh. 6.3 - Prob. 19ECh. 6.3 - Prob. 20ECh. 6.3 - Prob. 21ECh. 6.3 - Prob. 22ECh. 6.3 - Prob. 23ECh. 6.3 - Prob. 24ECh. 6.3 - Prob. 25ECh. 6.3 - Prob. 26ECh. 6.3 - Prob. 27ECh. 6.3 - Prob. 28ECh. 6.3 - Prob. 29ECh. 6.3 - Prob. 30ECh. 6.3 - Prob. 31ECh. 6.3 - Prob. 32ECh. 6.3 - Prob. 33ECh. 6.3 - Let T be the triangular region with vertices (0,...Ch. 6.3 - Prob. 35ECh. 6.3 - Prob. 36ECh. 6.3 - Use cylindrical shells to find the volume of the...Ch. 6.3 - Prob. 38ECh. 6.4 - Prob. 1ECh. 6.4 - Prob. 2ECh. 6.4 - Prob. 3ECh. 6.4 - Prob. 4ECh. 6.4 - Prob. 5ECh. 6.4 - Prob. 6ECh. 6.4 - Prob. 7ECh. 6.4 - Prob. 8ECh. 6.4 - Prob. 9ECh. 6.4 - Prob. 10ECh. 6.4 - Prob. 11ECh. 6.4 - Prob. 12ECh. 6.4 - Prob. 13ECh. 6.4 - Prob. 14ECh. 6.4 - Prob. 15ECh. 6.4 - Prob. 16ECh. 6.4 - Prob. 17ECh. 6.4 - Prob. 18ECh. 6.4 - Prob. 19ECh. 6.4 - Prob. 20ECh. 6.4 - Prob. 21ECh. 6.4 - Prob. 22ECh. 6.4 - Prob. 23ECh. 6.4 - Prob. 24ECh. 6.4 - Prob. 25ECh. 6.4 - Prob. 26ECh. 6.4 - Prob. 27ECh. 6.4 - Prob. 28ECh. 6.4 - Prob. 29ECh. 6.4 - Prob. 30ECh. 6.4 - Prob. 31ECh. 6.4 - Prob. 32ECh. 6.4 - Prob. 33ECh. 6.4 - Prob. 34ECh. 6.5 - Prob. 1ECh. 6.5 - Prob. 2ECh. 6.5 - Prob. 3ECh. 6.5 - Prob. 4ECh. 6.5 - Prob. 5ECh. 6.5 - Prob. 6ECh. 6.5 - (a) Find the average value of f on the given...Ch. 6.5 - Prob. 8ECh. 6.5 - Prob. 9ECh. 6.5 - Prob. 10ECh. 6.5 - If f is continuous and 13f(x)dx=8, show that f...Ch. 6.5 - Prob. 12ECh. 6.5 - Prob. 13ECh. 6.5 - Prob. 14ECh. 6.5 - Prob. 15ECh. 6.5 - Prob. 16ECh. 6.5 - Prob. 17ECh. 6.5 - Prob. 18ECh. 6.5 - Prob. 19ECh. 6.5 - Prob. 20ECh. 6.5 - Prob. 21ECh. 6.5 - Prob. 22ECh. 6.6 - Prob. 1ECh. 6.6 - Prob. 2ECh. 6.6 - Prob. 3ECh. 6.6 - Prob. 4ECh. 6.6 - Prob. 5ECh. 6.6 - Prob. 6ECh. 6.6 - Prob. 7ECh. 6.6 - Prob. 8ECh. 6.6 - Prob. 9ECh. 6.6 - Prob. 10ECh. 6.6 - Prob. 11ECh. 6.6 - Prob. 12ECh. 6.6 - Prob. 13ECh. 6.6 - Prob. 14ECh. 6.6 - Prob. 15ECh. 6.6 - Prob. 16ECh. 6.6 - Prob. 17ECh. 6.6 - Prob. 18ECh. 6.6 - Prob. 19ECh. 6.6 - Prob. 20ECh. 6.6 - Prob. 21ECh. 6.6 - Prob. 22ECh. 6.6 - Prob. 23ECh. 6.6 - Prob. 24ECh. 6.6 - Prob. 25ECh. 6.6 - Prob. 26ECh. 6.6 - Prob. 27ECh. 6.6 - Prob. 28ECh. 6.6 - Prob. 29ECh. 6.6 - Prob. 30ECh. 6.6 - Prob. 31ECh. 6.6 - Prob. 32ECh. 6.6 - Prob. 33ECh. 6.6 - Prob. 34ECh. 6.6 - Prob. 35ECh. 6.6 - Prob. 36ECh. 6.6 - Prob. 37ECh. 6.6 - Prob. 38ECh. 6.6 - Prob. 39ECh. 6.6 - Prob. 40ECh. 6.6 - Prob. 41ECh. 6.6 - Prob. 42ECh. 6.6 - Prob. 43ECh. 6.6 - Prob. 44ECh. 6.6 - Prob. 45ECh. 6.6 - Prob. 46ECh. 6.6 - Prob. 47ECh. 6.6 - Prob. 48ECh. 6.6 - Prob. 49ECh. 6.6 - Prob. 50ECh. 6.6 - Prob. 51ECh. 6.6 - Prob. 52ECh. 6.7 - Prob. 1ECh. 6.7 - Prob. 2ECh. 6.7 - Prob. 3ECh. 6.7 - Prob. 4ECh. 6.7 - Prob. 5ECh. 6.7 - Prob. 6ECh. 6.7 - Prob. 7ECh. 6.7 - Prob. 8ECh. 6.7 - Prob. 9ECh. 6.7 - Prob. 10ECh. 6.7 - Prob. 11ECh. 6.7 - Prob. 12ECh. 6.7 - Prob. 13ECh. 6.7 - Prob. 14ECh. 6.7 - Prob. 15ECh. 6.7 - Prob. 16ECh. 6.7 - Prob. 17ECh. 6.7 - Prob. 18ECh. 6.7 - Prob. 19ECh. 6.8 - Prob. 1ECh. 6.8 - Prob. 2ECh. 6.8 - Prob. 3ECh. 6.8 - Prob. 4ECh. 6.8 - Prob. 5ECh. 6.8 - Prob. 6ECh. 6.8 - Prob. 7ECh. 6.8 - Prob. 8ECh. 6.8 - Prob. 9ECh. 6.8 - Prob. 10ECh. 6.8 - Prob. 11ECh. 6.8 - Prob. 12ECh. 6.8 - Prob. 13ECh. 6.8 - Prob. 14ECh. 6.8 - Prob. 15ECh. 6.8 - Prob. 16ECh. 6.8 - Prob. 17ECh. 6.8 - Prob. 18ECh. 6 - (a) Draw two typical curves y = f(x) and y = g(x),...Ch. 6 - Suppose that Sue runs faster than Kathy throughout...Ch. 6 - Prob. 3RCCCh. 6 - Prob. 4RCCCh. 6 - Prob. 5RCCCh. 6 - Prob. 6RCCCh. 6 - Prob. 7RCCCh. 6 - Prob. 8RCCCh. 6 - Prob. 9RCCCh. 6 - Prob. 10RCCCh. 6 - Prob. 11RCCCh. 6 - Prob. 12RCCCh. 6 - Prob. 13RCCCh. 6 - Prob. 14RCCCh. 6 - Find the area of the region bounded by the given...Ch. 6 - Prob. 2RECh. 6 - Find the area of the region bounded by the given...Ch. 6 - Prob. 4RECh. 6 - Prob. 5RECh. 6 - Prob. 6RECh. 6 - Prob. 7RECh. 6 - Prob. 8RECh. 6 - Prob. 9RECh. 6 - Prob. 10RECh. 6 - Prob. 11RECh. 6 - Prob. 12RECh. 6 - Prob. 13RECh. 6 - Prob. 14RECh. 6 - Prob. 15RECh. 6 - Prob. 16RECh. 6 - Prob. 17RECh. 6 - Prob. 18RECh. 6 - The base of a solid is a circular disk with radius...Ch. 6 - Prob. 20RECh. 6 - Prob. 21RECh. 6 - (a) The base of a solid is a square with vertices...Ch. 6 - Prob. 23RECh. 6 - Prob. 24RECh. 6 - Prob. 25RECh. 6 - Prob. 26RECh. 6 - Prob. 27RECh. 6 - Prob. 28RECh. 6 - Prob. 29RECh. 6 - Prob. 30RECh. 6 - Prob. 31RECh. 6 - Prob. 32RECh. 6 - Prob. 33RECh. 6 - Prob. 34RECh. 6 - Prob. 35RECh. 6 - Prob. 36RECh. 6 - Prob. 37RECh. 6 - Prob. 38RECh. 6 - Prob. 39RECh. 6 - Prob. 1PCh. 6 - Prob. 2PCh. 6 - Prob. 3PCh. 6 - Prob. 4PCh. 6 - Prob. 5PCh. 6 - Prob. 6PCh. 6 - Prob. 7PCh. 6 - Prob. 8PCh. 6 - Prob. 9PCh. 6 - Prob. 10PCh. 6 - Prob. 11PCh. 6 - Prob. 12PCh. 6 - Prob. 13PCh. 6 - Prob. 14PCh. 6 - Prob. 15P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Can you answer this question and give step by step and why and how to get it. Can you write it (numerical method)arrow_forwardCan you answer this question and give step by step and why and how to get it. Can you write it (numerical method)arrow_forwardThere are three options for investing $1150. The first earns 10% compounded annually, the second earns 10% compounded quarterly, and the third earns 10% compounded continuously. Find equations that model each investment growth and use a graphing utility to graph each model in the same viewing window over a 20-year period. Use the graph to determine which investment yields the highest return after 20 years. What are the differences in earnings among the three investment? STEP 1: The formula for compound interest is A = nt = P(1 + − − ) n², where n is the number of compoundings per year, t is the number of years, r is the interest rate, P is the principal, and A is the amount (balance) after t years. For continuous compounding, the formula reduces to A = Pert Find r and n for each model, and use these values to write A in terms of t for each case. Annual Model r=0.10 A = Y(t) = 1150 (1.10)* n = 1 Quarterly Model r = 0.10 n = 4 A = Q(t) = 1150(1.025) 4t Continuous Model r=0.10 A = C(t) =…arrow_forward
- Use a graphing utility to find the point of intersection, if any, of the graphs of the functions. Round your result to three decimal places. (Enter NONE in any unused answer blanks.) y = 100e0.01x (x, y) = y = 11,250 ×arrow_forward5. For the function y-x³-3x²-1, use derivatives to: (a) determine the intervals of increase and decrease. (b) determine the local (relative) maxima and minima. (e) determine the intervals of concavity. (d) determine the points of inflection. (e) sketch the graph with the above information indicated on the graph.arrow_forwardCan you solve this 2 question numerical methodarrow_forward
- 1. Estimate the area under the graph of f(x)-25-x from x=0 to x=5 using 5 approximating rectangles Using: (A) right endpoints. (B) left endpoints.arrow_forward9. Use fundamental theorem of calculus to find the derivative d a) *dt sin(x) b)(x)√1-2 dtarrow_forward3. Evaluate the definite integral: a) √66x²+8dx b) x dx c) f*(2e* - 2)dx d) √√9-x² e) (2-5x)dx f) cos(x)dx 8)²₁₂√4-x2 h) f7dx i) f² 6xdx j) ²₂(4x+3)dxarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Area Between The Curve Problem No 1 - Applications Of Definite Integration - Diploma Maths II; Author: Ekeeda;https://www.youtube.com/watch?v=q3ZU0GnGaxA;License: Standard YouTube License, CC-BY