Chapter 6.2, Problem 40E

To determine

Find the volume of the described solid S.

Answer to Problem 40E

The volume of the described solid S is $\frac{\sqrt{3}}{12}$

Explanation of Solution

Given information: Given graph below:

Calculation:

  

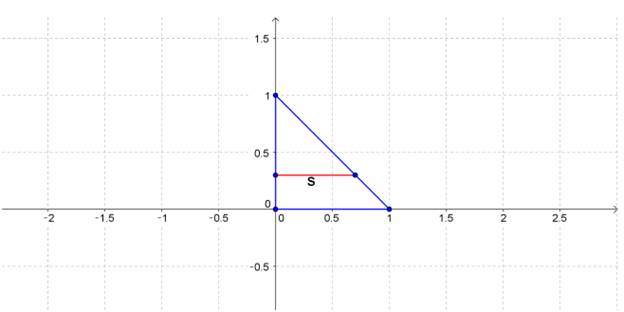
A cross section represents the side $s$ of an equilateral triangle. Recall that

The height of an equilateral triangle is

  $h=s\sin {60}^0=\frac{\sqrt{3}}{2}s$

So the area of one triangle is

  $A=\frac{1}{2}sh=\frac{1}{2}s\cdot \frac{\sqrt{3}}{2}s=\frac{\sqrt{3}}{4}{s}^2$

The equation of the line represent the diagonal is $y=-x+1\text{ or }x=-y+1$

I f we integrate along the $y$ -axis this will represent the $s$ values.

Integrate from $0\text{ to }1$

  $\begin{array}{l}V={\displaystyle \underset{0}{\overset{1}{\int }}\frac{\sqrt{3}}{4}}{s}^{2}dy\\ =\frac{\sqrt{3}}{4}{\displaystyle \underset{0}{\overset{1}{\int }}{\left(-y+1\right)}^2}dy\\ =\frac{\sqrt{3}}{4}{\displaystyle \underset{0}{\overset{1}{\int }}\left(y^2-2y+1\right)}dy\\ =\frac{\sqrt{3}}{4}{\left[\frac{1}{3}{y}^3-y^2+y\right]}_0^1\\ =\frac{\sqrt{3}}{4}\left[\frac{1}{3}-1+1-0\right]\\ =\frac{\sqrt{3}}{12}\end{array}$

Thu the volume of the described solid S is $\frac{\sqrt{3}}{12}$