
Locate the first positive root of
Where x is in radians. Use four iterations of the secant method with initial guesses of (a)
(a)
To calculate: Thefirst positive root of the function
Answer to Problem 7P
Solution:
The first positive root of the function
Explanation of Solution
Given Information:
The function,
Formula used:
The iterative equation of secant method is,
And, formula for approximate error is,
Calculation:
Consider the function,
For
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Similarly, all the iteration can be summarized as below,
| 0 | 3 | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Hence, the first positive root is
(b)
To calculate: The first positive root of the function
Answer to Problem 7P
Solution:
The first positive root of the function
Explanation of Solution
Given Information:
The function,
Formula used:
The iterative equation of secant method is,
And, formula for approximate error is,
Calculation:
Consider the function,
For
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Similarly, all the iteration can be summarized as below,
| 0 | 2.5 | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Hence, the first positive root is
(c)
To calculate: The first positive root of the function
Answer to Problem 7P
Solution:
The first positive root of the function
Explanation of Solution
Given Information:
The function,
Formula used:
The iterative equation of secant method is,
And, formula for approximate error is,
Calculation:
Consider the function,
For
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Similarly, all the iteration can be summarized as below,
| 0 | ||
| 1 | 16.76% | |
| 2 | ||
| 3 | ||
| 4 |
Hence, the first positive root is
(d)
The explanation of the result obtained by the secant method of the function
Answer to Problem 7P
Solution:
For the initial guesses
For the initial guesses
For the initial guesses
Explanation of Solution
Given Information:
The function,
Consider the function,
From part (a), the result obtained with the initial guesses
| 0 | 3 | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Use MATLAB to draw the graph of the function as below,
Code:
function f = g(x)
% f is assigned a value of function f(x).
f=sin(x)+cos(1+(x^2))-1;
%function is defined.
end
Output:
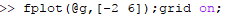
The graph obtained is,
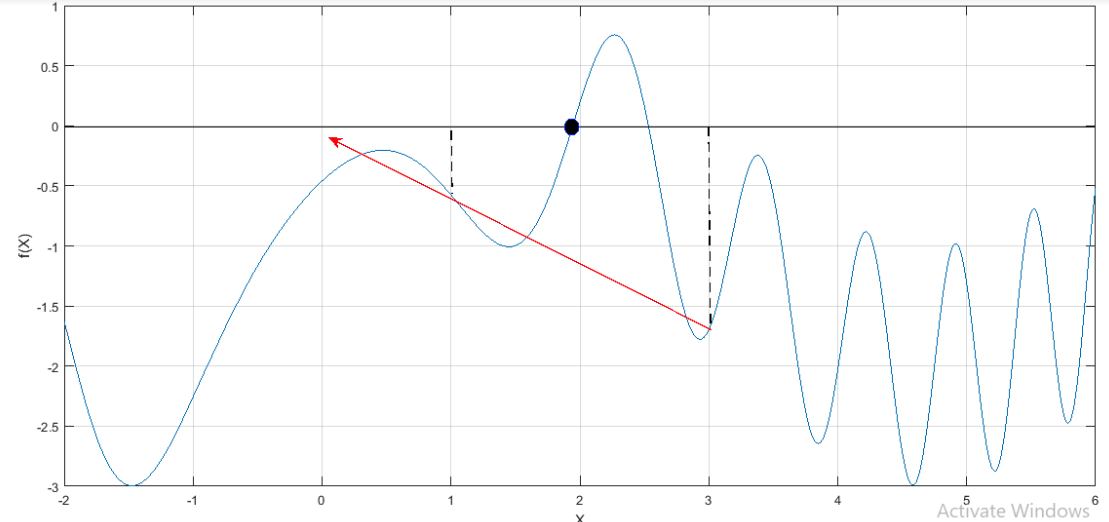
From the graph, it is observed that the first iteration gives a negative value due to the improper choice of initial guess.
From part (b), the result obtained with the initial guesses
| 0 | 2.5 | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Use MATLAB to draw the graph of the function as below,
Code:
function f = g(x)
% f is assigned a value of function f(x).
f=sin(x)+cos(1+(x^2))-1;
%function is defined.
end
Output:
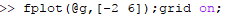
The graph obtained is,
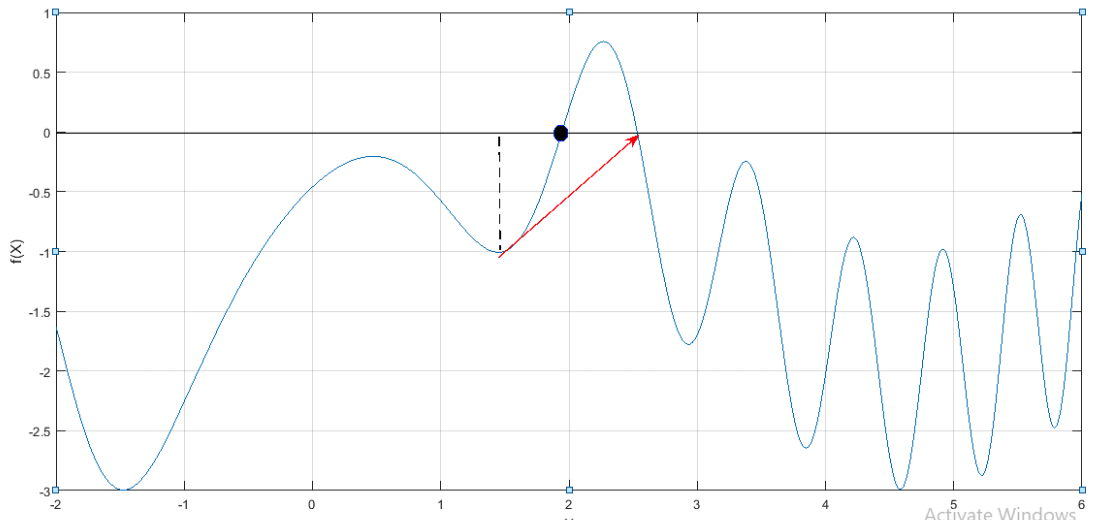
From the graph, it is observed that the root is converges towards the second positive root with these initial guesses instead of first positive root.
From part (c), the result obtained with the initial guesses
| 0 | ||
| 1 | 16.76% | |
| 2 | ||
| 3 | ||
| 4 |
Use MATLAB to draw the graph of the function as below,
Code:
function f = g(x)
% f is assigned a value of function f(x).
f=sin(x)+cos(1+(x^2))-1;
%function is defined.
Output:
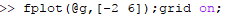
The graph obtained is,

From the graph, it is observed that the root is converges towards the first positive root with these initial guesses rapidly. Hence, these guesses are the proper selection to locate the first positive root by secant method.
Want to see more full solutions like this?
Chapter 6 Solutions
Numerical Methods for Engineers
Additional Math Textbook Solutions
College Algebra Essentials (5th Edition)
Thinking Mathematically (6th Edition)
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
Elementary Statistics: A Step By Step Approach
University Calculus: Early Transcendentals (4th Edition)
- Q/ Find the Laurent series of (2-3) cos around z = 1 2-1arrow_forward31.5. Let be the circle |+1| = 2 traversed twice in the clockwise direction. Evaluate dz (22 + 2)²arrow_forwardUsing FDF, BDF, and CDF, find the first derivative; 1. The distance x of a runner from a fixed point is measured (in meters) at an interval of half a second. The data obtained is: t 0 x 0 0.5 3.65 1.0 1.5 2.0 6.80 9.90 12.15 Use CDF to approximate the runner's velocity at times t = 0.5s and t = 1.5s 2. Using FDF, BDF, and CDF, find the first derivative of f(x)=x Inx for an input of 2 assuming a step size of 1. Calculate using Analytical Solution and Absolute Relative Error: = True Value - Approximate Value| x100 True Value 3. Given the data below where f(x) sin (3x), estimate f(1.5) using Langrage Interpolation. x 1 1.3 1.6 1.9 2.2 f(x) 0.14 -0.69 -0.99 -0.55 0.31 4. The vertical distance covered by a rocket from t=8 to t=30 seconds is given by: 30 x = Loo (2000ln 140000 140000 - 2100 9.8t) dt Using the Trapezoidal Rule, n=2, find the distance covered. 5. Use Simpson's 1/3 and 3/8 Rule to approximate for sin x dx. Compare the results for n=4 and n=8arrow_forward
- 1. A Blue Whale's resting heart rate has period that happens to be approximately equal to 2π. A typical ECG of a whale's heartbeat over one period may be approximated by the function, f(x) = 0.005x4 2 0.005x³-0.364x² + 1.27x on the interval [0, 27]. Find an nth-order Fourier approximation to the Blue Whale's heartbeat, where n ≥ 3 is different from that used in any other posts on this topic, to generate a periodic function that can be used to model its heartbeat, and graph your result. Be sure to include your chosen value of n in your Subject Heading.arrow_forward7. The demand for a product, in dollars, is p = D(x) = 1000 -0.5 -0.0002x² 1 Find the consumer surplus when the sales level is 200. [Hints: Let pm be the market price when xm units of product are sold. Then the consumer surplus can be calculated by foam (D(x) — pm) dx]arrow_forward4. Find the general solution and the definite solution for the following differential equations: (a) +10y=15, y(0) = 0; (b) 2 + 4y = 6, y(0) =arrow_forward
- 5. Find the solution to each of the following by using an appropriate formula developed in the lecture slides: (a) + 3y = 2, y(0) = 4; (b) dy - 7y = 7, y(0) = 7; (c) 3d+6y= 5, y(0) = 0arrow_forward1. Evaluate the following improper integrals: (a) fe-rt dt; (b) fert dt; (c) fi da dxarrow_forward8. Given the rate of net investment I(t) = 9t¹/2, find the level of capital formation in (i) 16 years and (ii) between the 4th and the 8th years.arrow_forward
- 9. If the marginal revenue function of a firm in the production of output is MR = 40 - 10q² where q is the level of output, and total revenue is 120 at 3 units of output, find the total revenue function. [Hints: TR = √ MRdq]arrow_forward6. Solve the following first-order linear differential equations; if an initial condition is given, definitize the arbitrary constant: (a) 2 + 12y + 2et = 0, y(0) = /; (b) dy+y=tarrow_forward4. Let A = {a, b, c, d, e, f}, B = {e, f, g, h} and C = {a, e, h,i}. Let U = {a, b, c, d, e, f, g, h, i, j, k}. • Draw a Venn Diagram to describe the relationships between these sets Find (AB) NC • Find (AC) UB Find AUBUC • Find (BC) N (A - C)arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning  Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning





