
Concept explainers
A single bead can slide with negligible friction on a stiff wire that has been bent into a circular loop of radius 15.0 cm as shown in Figure P6.48. The circle is always in a vertical plane and rotates steadily about its vertical diameter with a period of 0.450 s. The position of the bead is described by the angle θ that the radial line, from the center of the loop to the bead, makes with the vertical. (a) At what angle up from the bottom of the circle can the bead slay motionless relative to the turning circle? (b) What If? Repeat the problem, this time taking the period of the circle’s rotation as 0.850 s. (c) Describe how the solution to part (b) is different from the solution to part (a). (d) For any period or loop size, is there always an angle at which the bead can stand still relative to the loop? (e) Are there ever more than two angles? Arnold Arons suggested the idea for this problem.
Figure P6.48
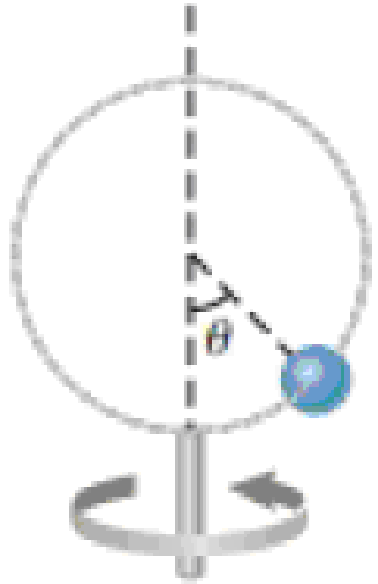
(a)
The angle from the bottom of the circle for which the bead can stay motionless.
Answer to Problem 68CP
The angles from the bottom of the circle for which the bead can stay motionless are
Explanation of Solution
Given info: The radius of the circular loop is
The acceleration due to gravity is
The rough sketch of the force body diagram of the situation is shown below,
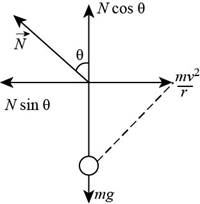
Figure (1)
The bead moves in a circle,
Here,
The speed of the bead is,
Here,
From the figure (1) the net force in
Here,
The net force in
Substitute
Substitute
The two possible solutions are,
and,
Substitute
Conclusion:
Therefore, the angles from the bottom of the circle for which the bead can stay motionless are
(b)
The angles from the bottom of the circle for which the bead can stay motionless for the time period as
Answer to Problem 68CP
The only one possible angle from the bottom of the circle for which the bead can stay motionless for time period
Explanation of Solution
Given info: The radius of the circular loop is
The acceleration due to gravity is
Form the part (a) equation (1).
The possible solutions are,
and,
Substitute
The above value is not possible.
Conclusion:
Therefore, the only one possible angle from the bottom of the circle for which the bead can stay motionless at time period
(c)
The difference between the solution of the part (a) and part (b).
Answer to Problem 68CP
The part (b) has only one solution as the time period is very large.
Explanation of Solution
Given info: The radius of the circular loop is
Form equation (1)
The possible solutions are,
and,
As the second solution depends directly on the square of the amplitude of the time period so, as the time period increases the value of
Conclusion:
Therefore, the part (b) has only one solution as the time period is very large.
(d)
The angle at which the bead can stand still relative to the loop.
Answer to Problem 68CP
The angle for which condition
Explanation of Solution
Given info: The radius of the circular loop is
Form equation (1)
The possible solutions are,
and,
As the range of the cosine function is
So, the value of the cosine of the angle is always less than
Conclusion:
Therefore, for the condition
(e)
Whether there are more than two angles.
Answer to Problem 68CP
The number of possible angles are
Explanation of Solution
Given info: The radius of the circular loop is
Form equation (1)
The possible solutions are,
and,
Form the above expression the second solution depends on time period, acceleration due to gravity and the radius of the hoop and for a given case the parameters has only one value so the second solution has only one answer.
Conclusion:
Therefore, the number of possible angles are
Want to see more full solutions like this?
Chapter 6 Solutions
Bundle: Physics for Scientists and Engineers with Modern Physics, Loose-leaf Version, 9th + WebAssign Printed Access Card, Multi-Term
Additional Science Textbook Solutions
College Physics: A Strategic Approach (3rd Edition)
Campbell Biology (11th Edition)
Human Biology: Concepts and Current Issues (8th Edition)
Introductory Chemistry (6th Edition)
Fundamentals Of Thermodynamics
- No chatgpt pls will upvotearrow_forwardneed help part earrow_forwardCritical damping is the case where the mass never actually crosses over equilibrium position, but reaches equilibrium as fast as possible. Experiment with changing c to find the critical damping constant. Use the same initial conditions as in the last problem. Zoom in a bit to make sure you don't allow any oscillations to take place - even small ones.arrow_forward
- NASA's KC-135 Reduced Gravity Research aircraft, affectionately known as the "Vomit Comet," is used in training astronauts and testing equipment for microgravity environments. During a typical mission, the aircraft makes approximately 30 to 40 parabolic arcs. During each arc, the aircraft and objects inside it are in free-fall, and passengers float freely in apparent "weightlessness." The figure below shows the altitude of the aircraft during a typical mission. It climbs from 24,000 ft to 30,850 ft, where it begins a parabolic arc with a velocity of 155 m/s at 45.0° nose-high and exits with velocity 155 m/s at 45.0° nose-low. 31 000 45° nose high 45° nose low 24 000 Zero g 65 Maneuver time (s) (a) What is the aircraft's speed (in m/s) at the top of the parabolic arc? 110.0 m/s (b) What is the aircraft's altitude (in ft) at the top of the parabolic arc? 2.04e+04 What is the initial height at the start of the parabolic arc? What is the initial velocity at this point? What is the final…arrow_forward12. What could we conclude if a system has a phase trajectory that sweeps out larger and larger area as time goes by?arrow_forwardneed help part darrow_forward
- A cab driver heads south with a steady speed of v₁ = 20.0 m/s for t₁ = 3.00 min, then makes a right turn and travels at v₂ = 25.0 m/s for t₂ = 2.80 min, and then drives northwest at v3 = 30.0 m/s for t3 = 1.00 min. For this 6.80-min trip, calculate the following. Assume +x is in the eastward direction. (a) total vector displacement (Enter the magnitude in m and the direction in degrees south of west.) magnitude direction For each straight-line movement, model the car as a particle under constant velocity, and draw a diagram of the displacements, labeling the distances and angles. Let the starting point be the origin of your coordinate system. Use the relationship speed = distance/time to find the distances traveled during each segment. Write the displacement vector, and calculate its magnitude and direction. Don't forget to convert min to s! m Model the car as a particle under constant velocity, and draw a diagram of the displacements, labeling the distances and angles. Let the…arrow_forwardî A proton is projected in the positive x direction into a region of uniform electric field E = (-5.50 x 105) i N/C at t = 0. The proton travels 7.20 cm as it comes to rest. (a) Determine the acceleration of the proton. magnitude 5.27e13 direction -X m/s² (b) Determine the initial speed of the proton. 8.71e-6 magnitude The electric field is constant, so the force is constant, which means the acceleration will be constant. m/s direction +X (c) Determine the time interval over which the proton comes to rest. 1.65e-7 Review you equations for constant accelerated motion. sarrow_forwardThree charged particles are at the corners of an equilateral triangle as shown in the figure below. (Let q = 2.00 μC, and L = 0.750 m.) y 7.00 με 60.0° L 9 -4.00 μC x (a) Calculate the electric field at the position of charge q due to the 7.00-μC and -4.00-μC charges. 112 Once you calculate the magnitude of the field contribution from each charge you need to add these as vectors. KN/CI + 64 × Think carefully about the direction of the field due to the 7.00-μC charge. KN/Cĵ (b) Use your answer to part (a) to determine the force on charge q. 240.0 If you know the electric field at a particular point, how do you find the force that acts on a charge at that point? mN Î + 194.0 × If you know the electric field at a particular point, how do you find the force that acts on a charge at that point? mNarrow_forward
- In the Donkey Kong Country video games you often get around by shooting yourself out of barrel cannons. Donkey Kong wants to launch out of one barrel and land in a different one that is a distance in x of 9.28 m away. To do so he launches himself at a velocity of 22.6 m/s at an angle of 30.0°. At what height does the 2nd barrel need to be for Donkey Kong to land in it? (measure from the height of barrel 1, aka y0=0)arrow_forwardFor which value of θ is the range of a projectile fired from ground level a maximum? 90° above the horizontal 45° above the horizontal 55° above the horizontal 30° above the horizontal 60° above the horizontalarrow_forwardA map from The Legend of Zelda: The Breath of the Wild shows that Zora's Domain is 7.55 km in a direction 25.0° north of east from Gerudo Town. The same map shows that the Korok Forest is 3.13 km in a direction 55.0° west of north from Zora's Domain. The figure below shows the location of these three places. Modeling Hyrule as flat, use this information to find the displacement from Gerudo Town to Korok Forest. What is the magnitude of the displacement? Find the angle of the displacement. Measure the angle in degrees north of east of Gerudo Town.arrow_forward
 Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University





