Power System Analysis and Design (MindTap Course List)
6th Edition
ISBN: 9781305632134
Author: J. Duncan Glover, Thomas Overbye, Mulukutla S. Sarma
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 6, Problem 6.30P
Determine the bus admittance matrix
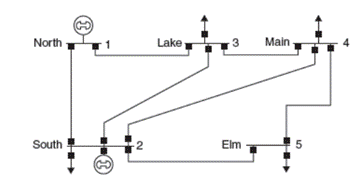
TABLE 6.11
Bus input data for Problem 6.20
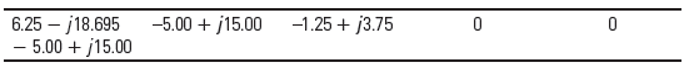
TABLE 6.12
Partially Completed Bus Admittance Matrix
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Figure 6.12 shows the one-line diagram of a simple three-bus power system with
generators at buses 1 and 3. The magnitude of voltage at bus 1 is adjusted to 1.05
pu. Voltage magnitude at bus 3 is fixed at 1.04 pu with a real power generation
of 200 MW. A load consisting of 400 MW and 250 Mvar is taken from bus 2.
Line impedances are marked in per unit on a 100 MVA base, and the line charging
susceptances are neglected. Obtain the power flow solution by the Gauss-Seidel
method including line flows and line losses.
1
2
0.02 + j0.04
400
MW
0.01 + j0.03
0.0125 + j0.025
250
Mvar
Slack Bus
3
V = 1.0520°
200
MW
| V3 = 1.04
Figure 6.12
6.32 For a two-bus power system, a 0.7 + j0.4 per unit load at bus 2 is supplied
by a generator at bus 1 through a transmission line with series impedance
of 0.05 + j0.1 per unit. With bus 1 as the slack bus with a fixed per-unit
voltage of 1.0/0, use the Gauss-Seidel method to calculate the voltage at
bus 2 after three iterations.
Problem 6.2: A 3000 kVA, 3-phase transformer bank steps down line voltage
from 12.5 kV to 480 V. The HV side is connected in A and the LV side in
grounded Y. Determine (a) the HV side line and phase currents, and (b)
the LV side line and phase currents.
Chapter 6 Solutions
Power System Analysis and Design (MindTap Course List)
Ch. 6 - For a set of linear algebraic equations in matrix...Ch. 6 - For an NN square matrix A, in (N1) steps, the...Ch. 6 - Prob. 6.9MCQCh. 6 - Prob. 6.11MCQCh. 6 - Using Gauss elimination, solve the following...Ch. 6 - Prob. 6.9PCh. 6 - Determine the bus admittance matrix (Ybus) for the...Ch. 6 - Prob. 6.34PCh. 6 - Prob. 6.37PCh. 6 - Prob. 6.38P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, electrical-engineering and related others by exploring similar questions and additional content below.Similar questions
- 6.11. In the two-bus system shown in Figure 6.24, bus 1 is a slack bus with V₁ = 1.020° pu. A load of 100 MW and 50 Mvar is taken from bus 2. The line impedance is z12 = 0.12 + j0.16 pu on a base of 100 MVA. Using Newton- Raphson method, obtain the voltage magnitude and phase angle of bus 2. Start with an initial estimate of |V₂|(0) = 1.0 pu and 8₂ (0) two iterations. 0°. Perform 2 *12 = 0 12 + j0.16 Note 100 MW -+-) 50 Myar Perform Second iteration I have problem while solving it 어 V = 1.040° FIGURE 6.24 One-line diagram for Problem 6.11.. U(¹) = 0.8 Pu ops 62 = -1.0 radionarrow_forward6.11. In the two-bus system shown in Figure 6.24, bus 1 is a slack bus with V₁ = 1.020° pu. A load of 100 MW and 50 Mvar is taken from bus 2. The line impedance is 212 0.12 + j0.16 pu on a base of 100 MVA. Using Newton- Raphson method, obtain the voltage magnitude and phase angle of bus 2. Start with an initial estimate of |V₂|(0) 1.0 pu and 5₂ (0) two iterations. 0°. Perform Note 212 0.12 + 30.16 +100 MW nghiệm 50 Mvar Perform Second iteration I have problem Y, while solving it 어 V₁ = 1.040° FIGURE 6.24 One-line diagram for Problem 6.11. V(i) = 0.8 Pu 62") = -1.0 radionarrow_forwardFor the system in Figure 4 with given generation and load dispatch determine the voltages after two itterations of Gauss-Seidel method. Assume the initial voltage to be 1.01 at angle of 0◦ pu at bus 1, 1.015 at angle of 0◦ pu at bus 2, and 1.0 at angle of 0◦ pu at bus 3. All line impedances are in per unit on a common base, and charging is neglected. Take base power of 100 MVA.arrow_forward
- The equivalent circuit of a single phase short transmission line is shown in Figure Q4 (b). Here, the total line resistance and inductance are shown as lumped instead of being distributed. i) Sketch the phasor diagram and assess with by labeling the details for the A.C. series circuit shown in Figure Q4 (b) for the lagging power factor at load point (Vn). ii) Summarize, the impact of voltage regulation and efficiency, if the line resistance and line increases are doubled Figure Q4(b). R XL Vs Vn Figure Q4(b) Loadarrow_forward6.5. A three phase 50 Hz transmission line has impedance of (25.3 + j66.5) ohms and a shunt admittance of 4.42 x 10 mho per phase. If it delivers a load of 50 MW at 220 kV at 0.8 power factor lagging, determine the sending end voltage (a) by short line approximation (b) nominal II method (c) exact transmission line equations. Ans. (a) 233.8 2.2° kV, (b) 232.2 2.33°, (c) 230.52 2.50° kV,arrow_forwardQ6: A five-bus network has generators at buses 1 and 3 rated 270 and 225 MVA, respectively. The generator sub-transient reactances plus the reactances of the transformers connecting them to the buses are each 0.3 pu on the generator rating as base. The turns ratios of the transformers are such that the voltage base in each generator circuit is equal to the voltage rating of the generator. Line impedances in pu on a 100 MVA system base are shown in Fig. below. All resistances are neglected. Using the bus impedance matrix for the network which includes the generator and transformer reactances, find the sub-transient current in a three phase fault at bus 4 and the current coming to the faulted bus over each line. Prefault current is to be neglected and all voltages are assumed to be 1 pu before the fault occurs. (2) 3 j0.126 1.0/0° j0.168 0/0° j0.1111 lll j0.1333 j0.210 ell j0.126 ll j0.252 4 j0.336 helltearrow_forward
- Q4(b) The equivalent circuit of a single phase short transmission line is shown in Figure Q4(b). Here, the total line resistance and inductance are shown as lumped instead of being distributed. i) Sketch the phasor diagram and assess with by labeling the details for the A.C. series circuit shown in Figure Q4(b) for the lagging power factor at load point (Vn). ii) Summarize, what if the load change from low value to high value shown in Figure Q4(b). R XL el Vs Vn Figure Q4(b) Loadarrow_forwardProblem 6.7 book power system analysis by hadi sadaatarrow_forward6.6. In the power system network shown in Figure 6.5, bus 1 is a slack bus with V = 1.020° per unit and bus 2 is a load bus with S2 = 280 MW + j60 Mvar. The line impedance on a base of 100 MVA is Z = 0.02 + j0.04 per unit. (a) Using Gauss-Seidel method, determine Va. Use an initial estimate of V 1.0 + j0.0 and perform four iterations. (b) If after several iterations voltage at bus 2 converges to V, = 0.90 j0.10, determine S, and the real and reactive power loss in the line. %3D S1 Z12 0.02+ j0.04 2 1 S2 280 MW +j60 Mvararrow_forward
- You are given that the system shown in Figure 4.25 has a 110/220 kV autotransformer. The positive- and zero-sequence impedances in ohms or percent are as shown in the figure, the zero-sequence impedances being in parentheses. Assume that the low- voltage system is solidly grounded. For a phase-a-to-ground fault at the midpoint of the transmission line, calculate the transformer current In in the neutral and the phase a currents Ia and I'a on the high and low sides of the transformer. If the source on the low-voltage side is to be grounded through a reactance, determine the value of the grounding reactance for which the transformer neutral current becomes zero. As the grounding reactance changes around this value, the direction of the neutral current will reverse, and will affect the polarizing capability of the neutral current for ground faults on the high side. Can faults on the low-voltage side ever cause the neutral current to reverse?arrow_forwardTransmission line conductance is usually neglected in power system studies. True Falsearrow_forwardFigure 4.34 shows double-circuit conductors' relative positions in segment I of transposition of a completely transposed three-phase overhead transmission line. The inductance is given by L=2107lnGMDGMRH/m/phase Where GMD=(DABeqDBCeqDACeq)1/3 With mean distances defined by equivalent spacings DABeq=(D12D12D12D12)1/4DBCeq=(D23D23D23D13)1/4DACeq=(D13D13D13)1/4 And GMR=[ (GMR)A(GMR)B(GMR)C ]1/3 with phase GMRs defined by (GMR)A=[ rD11 ]1/2;(GMR)B=[ rD22 ]1/2;(GMR)C=[ rD33 ]1/2 and r is the GMR of phase conductors. Now consider a 345-kV, three-phase, double-circuit line with phase-conductors GMR of 0.0588 ft and the horizontal conductor configuration shown in Figure 4.35. Determine the inductance per meter per phase in Henries (H). Calculate the inductance of just one circuit and then divide by 2 to obtain the inductance of the double circuit.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Power System Analysis and Design (MindTap Course ...Electrical EngineeringISBN:9781305632134Author:J. Duncan Glover, Thomas Overbye, Mulukutla S. SarmaPublisher:Cengage Learning
Power System Analysis and Design (MindTap Course ...
Electrical Engineering
ISBN:9781305632134
Author:J. Duncan Glover, Thomas Overbye, Mulukutla S. Sarma
Publisher:Cengage Learning
How do Electric Transmission Lines Work?; Author: Practical Engineering;https://www.youtube.com/watch?v=qjY31x0m3d8;License: Standard Youtube License