Chapter 6, Problem 6.1CTP

Since laboratory or field experiments are generally expensive and time consuming, geotechnical engineers often have to rely on empirical relationships to predict design parameters. Section 6.6 presents such relationships for predicting optimum moisture content and maximum dry unit weight. Let us use some of these equations and compare our results with known experimental data. The following table presents the results from laboratory compaction tests conducted on a wide range of fine-grained soils using various compactive efforts (E). Based on the soil data given in the table, determine the optimum moisture content and maximum dry unit weight using the empirical relationships presented in Section 6.6.

1. a. Use the Osman et al. (2008) method [Eqs. (6.15) through (6.18)].
2. b. Use the Gurtug and Sridharan (2004) method [Eqs. (6.13) and (6.14)].
3. c. Use the Matteo et al. (2009) method [Eqs. (6.19) and (6.20)].
4. d. Plot the calculated w_opt against the experimental w_opt, and the calculated γ_d(max) with the experimental γ_d(max). Draw a 45° line of equality on each plot.
5. e. Comment on the predictive capabilities of various methods. What can you say about the inherent nature of empirical models?

To determine

Find the optimum moisture content and maximum dry unit weight using Osman et al. (2008) method.

Explanation of Solution

Calculation:

Determine the plasticity index PI using the relation.

$PI=LL-PL$

Here, LL is the liquid limit for soil 1 and PL is the plastic limit for soil 1.

Substitute 17 % for LL and 16 % for PL.

$\begin{array}{c}PI=17-16\\ =1\%\end{array}$

Similarly, calculate the PI for remaining soils.

Determine the optimum moisture content for soil 1 using the relation.

$w_{\text{opt}}=\left(1.99-0.165\ln E\right)\left(PI\right)$

Here, E is the compaction energy for soil 1.

Substitute $2,700{\text{kN-m/m}}^{\text{3}}$ for E and 1 % for PI.

$\begin{array}{c}{w}_{\text{opt}}=\left(1.99-0.165\ln 2,700\right)\left(1\right)\\ =0.69\%\end{array}$

Similarly, calculate the optimum moisture content for remaining soils.

Determine the value of L using the relation.

$L=14.34+1.195\ln E$

Substitute $2,700{\text{kN-m/m}}^{\text{3}}$ for E.

$\begin{array}{c}L=14.34+1.195\ln 2,700\\ =23.78\end{array}$

Determine the value of M using the relation.

$M=-0.19+0.073\ln E$

Substitute $2,700{\text{kN-m/m}}^{\text{3}}$ for E.

$\begin{array}{c}M=-0.19+0.073\ln 2,700\\ =0.387\end{array}$

Determine the maximum dry unit weight of the soil 1 using the relation.

${\gamma }_{d\left(\max \right)}=L-M{w}_{\text{opt}}$

Substitute 23.78 for L, 0.387 for M, and 0.69 % for $w_{\text{opt}}$.

$\begin{array}{c}{\gamma }_{d\left(\max \right)}=23.78-0.387\times 0.69\\ =23.51{\text{kN/m}}^{\text{3}}\end{array}$

Similarly, calculate the maximum dry unit weight for remaining soils.

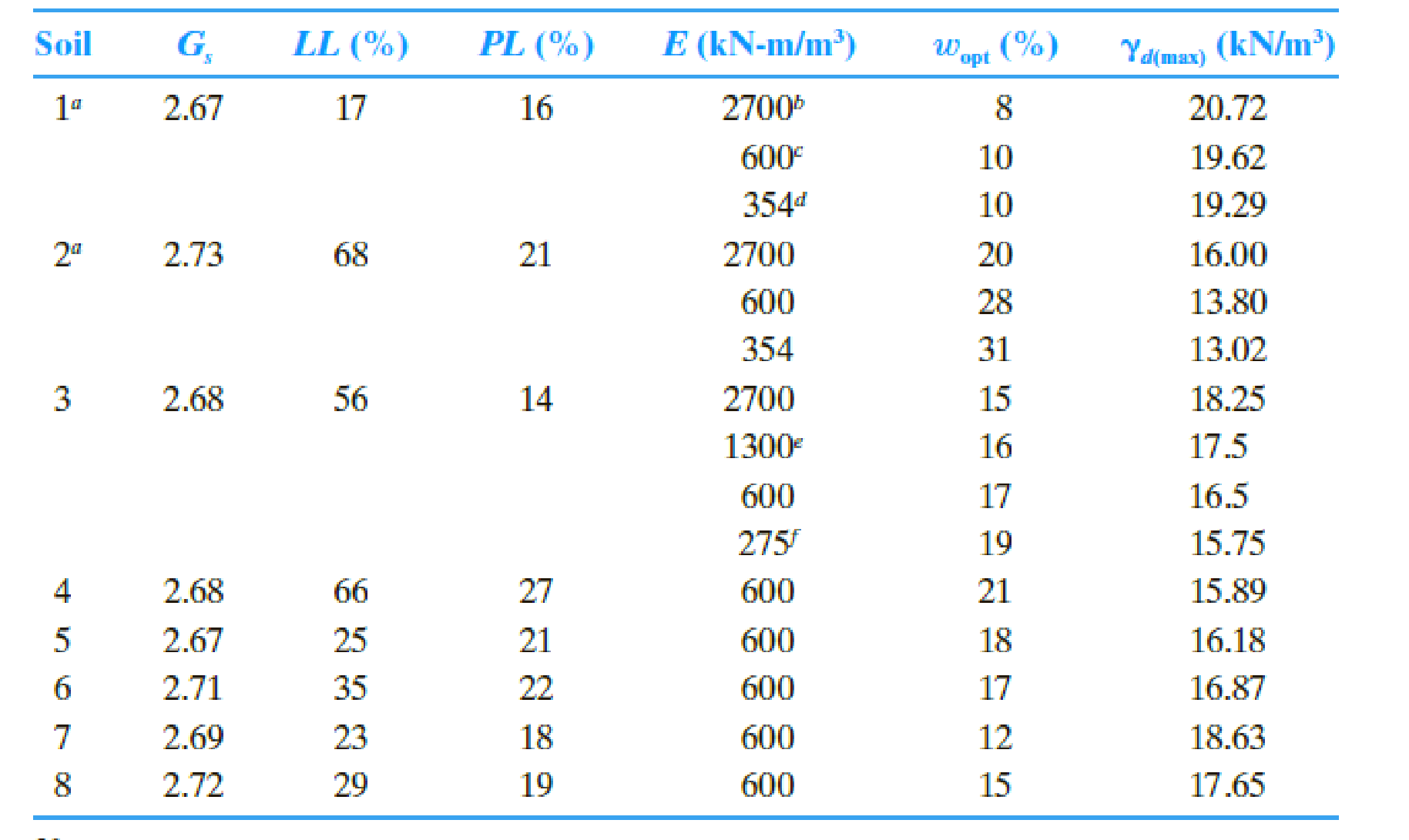
Summarize the calculated values as in Table 1.

Soil	LL (%)	PL (%)	PI (%)	E $\left({\text{kN-m/m}}^{\text{3}}\right)$	$w_{\text{opt}}$(%) (Exp)	${\gamma }_{d\left(\max \right)}$ $\left({\text{kN/m}}^{\text{3}}\right)$ (Exp)	$w_{\text{opt}}$(%)	L	M	${\gamma }_{d\left(\max \right)}$$\left({\text{kN/m}}^{\text{3}}\right)$
1	17	16	1	2,700	8	20.72	0.69	23.782	0.387	23.51
				600	10	19.62	0.93	21.984	0.277	21.73
				354	10	19.29	1.02	21.354	0.238	21.11
2	68	21	47	2,700	20	16.00	32.26	23.782	0.387	11.30
				600	28	13.80	43.92	21.984	0.277	9.82
				354	31	13.02	48.01	21.354	0.238	9.91
3	56	14	42	2,700	15	18.25	28.82	23.782	0.387	12.63
				1,300	16	17.50	33.89	22.908	0.333	11.61
				600	17	16.50	39.24	21.984	0.277	11.12
				275	19	15.75	44.65	21.052	0.220	11.23
4	66	27	39	600	21	15.89	36.45	21.984	0.277	11.89
5	25	21	4	600	18	16.18	3.740	21.984	0.277	20.95
6	35	22	13	600	17	16.87	12.15	21.984	0.277	18.62
7	23	18	5	600	12	18.63	4.67	21.984	0.277	20.69
8	29	19	10	600	15	17.65	9.35	21.984	0.277	19.39

To determine

Find the optimum moisture content and maximum dry unit weight using Gurtug and Sridharan (2004) method.

Explanation of Solution

Calculation:

Determine the optimum moisture content for soil 1 using the relation.

$w_{\text{opt}}=\left(1.95-0.38\left(\log E\right)\right)\left(PL\right)$

Substitute $2,700{\text{kN-m/m}}^{\text{3}}$ for E and 16 % for PL.

$\begin{array}{c}{w}_{\text{opt}}=\left(1.95-0.38\left(\log 2,700\right)\right)16\\ =10.34\%\end{array}$

Determine the maximum dry unit weight of the soil 1 using the relation.

${\gamma }_{d\left(\max \right)}=22.68e^{-0.0183w_{\text{opt}}}$

Substitute 10.34 % for $w_{\text{opt}}$.

$\begin{array}{c}{\gamma }_{d\left(\max \right)}=22.68e^{-0.0183\times 10.34}\\ =18.77{\text{kN/m}}^{\text{3}}\end{array}$

Similarly, calculate the maximum dry unit weight for remaining soils.

Summarize the calculated values as in Table 2.

Soil	PL (%)	E $\left({\text{kN-m/m}}^{\text{3}}\right)$	$w_{\text{opt}}$(%) (Exp)	${\gamma }_{d\left(\max \right)}$ $\left({\text{kN/m}}^{\text{3}}\right)$ (Exp)	$w_{\text{opt}}$(%)	${\gamma }_{d\left(\max \right)}$$\left({\text{kN/m}}^{\text{3}}\right)$
1	16	2,700	8	20.72	10.34	18.77
		600	10	19.62	14.31	17.46
		354	10	19.29	15.70	17.02
2	21	2,700	20	16.00	13.57	17.69
		600	28	13.80	18.78	16.08
		354	31	13.02	20.61	15.55
3	14	2,700	15	18.25	9.05	19.22
		1,300	16	17.50	10.73	18.64
		600	17	16.50	12.52	18.04
		275	19	15.75	14.32	17.45
4	27	600	21	15.89	24.15	14.58
5	21	600	18	16.18	18.78	16.08
6	22	600	17	16.87	19.67	15.82
7	18	600	12	18.63	16.10	16.89
8	19	600	15	17.65	16.99	16.62

To determine

Find the optimum moisture content and maximum dry unit weight using Matteo et al. method.

Explanation of Solution

Calculation:

Determine the optimum moisture content for soil 1 using the relation.

$w_{\text{opt}}=-0.86\left(LL\right)+3.04\left(\frac{LL}{G_s}\right)+2.2$

Substitute 17 % LL and $2.67$ for $G_s$.

$\begin{array}{c}{w}_{\text{opt}}=-0.86\left(17\right)+3.04\left(\frac{17}{2.67}\right)+2.2\\ =6.94\%\end{array}$

Determine the maximum dry unit weight of the soil 1 using the relation.

${\gamma }_{d\left(\max \right)}=40.316\left(w_{\text{opt}}^{-0.295}\right)\left(P{I}^{0.032}\right)-2.4$

Substitute 6.94 % for $w_{\text{opt}}$ and 1 % for PI.

$\begin{array}{c}{\gamma }_{d\left(\max \right)}=40.316\left({6.94}^{-0.295}\right)\left(1^{0.032}\right)-2.4\\ =20.37{\text{kN/m}}^{\text{3}}\end{array}$

Similarly, calculate the maximum dry unit weight for remaining soils.

Summarize the calculated values as in Table 3.

Soil	Specific gravity $\left(G_s\right)$	PI (%)	$w_{\text{opt}}$(%) (Exp)	${\gamma }_{d\left(\max \right)}$ $\left({\text{kN/m}}^{\text{3}}\right)$ (Exp)	$w_{\text{opt}}$(%)	${\gamma }_{d\left(\max \right)}$$\left({\text{kN/m}}^{\text{3}}\right)$
1	2.67	1	8	20.72	6.94	20.37
			10	19.62	6.94	20.37
			10	19.29	6.94	20.37
2	2.73	47	20	16.00	19.44	16.60
			28	13.80	19.44	16.60
			31	13.02	19.44	16.60
3	2.68	42	15	18.25	17.56	17.11
			16	17.50	17.56	17.11
			17	16.50	17.56	17.11
			19	15.75	17.56	17.11
4	2.68	39	21	15.89	20.31	16.25
5	2.67	4	18	16.18	9.16	19.52
6	2.71	13	17	16.87	11.36	18.97
7	2.69	5	12	18.63	8.41	20.25
8	2.72	10	15	17.65	9.67	19.82

To determine

Plot the graph between the calculated $w_{\text{opt}}$ values versus experimental $w_{\text{opt}}$ values, and the calculated ${\gamma }_{d\left(\max \right)}$ values versus experimental ${\gamma }_{d\left(\max \right)}$ values. Draw the $45°$ line of equality on the each plot.

Explanation of Solution

Refer Table 1, 2, and 3.

Draw the graph between the calculated $w_{\text{opt}}$ values versus experimental $w_{\text{opt}}$ values as in Figure 1.

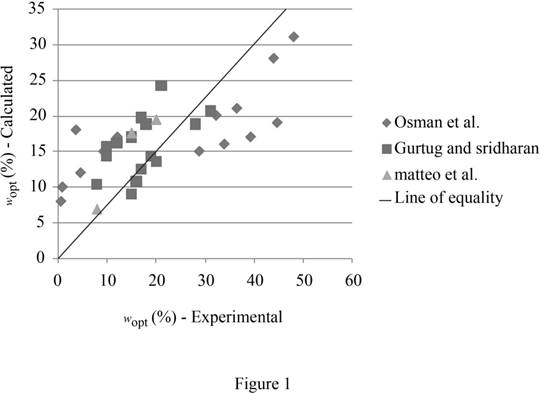
Draw the graph between calculated ${\gamma }_{d\left(\max \right)}$ values versus experimental ${\gamma }_{d\left(\max \right)}$ values as in Figure 2.

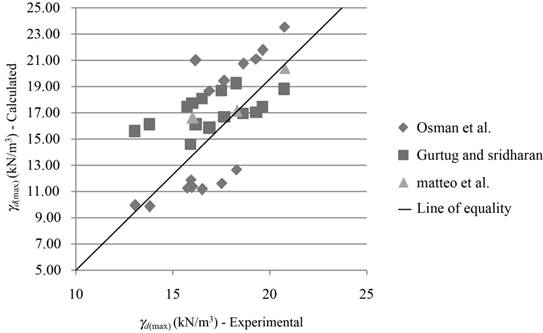
To determine

Comment on the predictive capabilities of various methods and comment about the inherent nature of empirical models.

Explanation of Solution

Prediction of optimum moisture content:

Refer Figure (1), several data points are closely packed around the $45°$ line for both the method of Osman et al. (2008) and Gurtug and Sridharan (2004) models signifying reasonable agreement between the calculated and experimental values. For the remaining soils, a poor agreement is observed. The one point from the Matteo method in the model plot showing the close agreement near the equality line and the other two points are slightly away from the equality line.

Prediction of maximum dry unit weight:

Most data points for all models show good covenant between the calculated and the experimental values.

The empirical models are often limited to the materials, test methods and environmental conditions under which the experiments were conducted and the developed models. For new materials and conditions, the predicted values may not be reliable.