Chapter 6, Problem 6.156QP

We hear a lot about how the burning of hydrocarbons produces the greenhouse gas CO₂, but what about the effect of increasing energy consumption on the amount of oxygen in the atmosphere required to sustain life? The figure shows past and projected world energy consumption. (a) How many moles of oxygen would be required to generate the additional energy expenditure for the next decade? (b) What would be the resulting decrease in atmospheric oxygen?

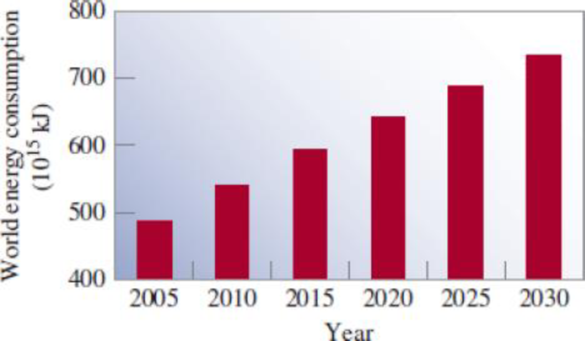
Interpretation Introduction

Interpretation:

The number of moles oxygen that would be required to generate the additional energy expenditure for the next decade has to be calculated.

Explanation of Solution

The raise in energy consumption is roughly ${\text{100×10}}^{\text{15}}\text{kJ}$ per decade.  Assume the raise in energy comes from the combustion of octane

${\text{C}}_{\text{8}}{\text{H}}_{\text{18(l)}}\text{+}\frac{\text{25}}{\text{2}}{\text{O}}_{\text{2(g)}}\stackrel{}{\to }{\text{8CO}}_{\text{2(g)}}{\text{+9H}}_{\text{2}}{\text{O}}_{\left(\text{l}\right)}\text{ΔH°=-5500}\text{kJ/mole}$

The mass of oxygen gas required to support the increase in energy assumption for one decade is calculated below,

$\begin{array}{l}\text{Mass}\text{of}\text{oxygen}\text{=}{\text{100×10}}^{\text{15}}\text{kJ×}\frac{\text{1}\text{mole}{\text{C}}_{\text{8}}{\text{H}}_{\text{18}}}{\text{5500}\text{kJ}}\text{×}\frac{\frac{\text{25}}{\text{2}}\text{mole}{\text{O}}_{\text{2}}}{\text{1}\text{mole}{\text{C}}_{\text{8}}{\text{H}}_{\text{18}}}\text{×}\frac{\text{32}\text{g}{\text{O}}_{\text{2}}}{\text{1}\text{mole}{\text{O}}_{\text{2}}}\\ \text{=}{\text{7×10}}^{\text{15}}\text{g}{\text{O}}_{\text{2}}\end{array}$

The total mass of atmosphere is ${\text{5×10}}^{\text{15}}\text{kg}\text{.}$  Since the atmosphere is roughly $\text{20\%}{\text{O}}_{\text{2}}$ and $\text{80\%}{\text{N}}_{\text{2}}$ moles of gas, the average mass percent of oxygen in the atmosphere is calculated as,

$\frac{\text{20}\text{mole}{\text{O}}_{\text{2}}\text{×32}\text{g/mole}}{\left(\text{20}\text{mole}{\text{O}}_{\text{2}}\text{×32}\text{g/mole}\right)\text{+}\left(\text{80}\text{mole}{\text{N}}_{\text{2}}\text{×28}\text{g/mole}\right)}\text{×100\%}\text{=}\text{22\%}{\text{O}}_{\text{2}}\text{by}\text{mass}$

Therefore, the mass of oxygen in the atmosphere is,

${\text{5×10}}^{\text{18}}\text{kg×}\frac{\text{1000}\text{g}}{\text{1}\text{kg}}\text{×0}\text{.22}\text{=}{\text{1×10}}^{\text{21}}{\text{gO}}_{\text{2}}$

The mass of oxygen in the atmosphere is ${\text{1×10}}^{\text{21}}\text{g}\text{.}$

Interpretation Introduction

Interpretation:

The resulting decrease in the atmospheric oxygen has to be given.

Explanation of Solution

The raise in energy consumption is roughly ${\text{100×10}}^{\text{15}}\text{kJ}$ per decade.  Assume the raise in energy comes from the combustion of octane

${\text{C}}_{\text{8}}{\text{H}}_{\text{18(l)}}\text{+}\frac{\text{25}}{\text{2}}{\text{O}}_{\text{2(g)}}\stackrel{}{\to }{\text{8CO}}_{\text{2(g)}}{\text{+9H}}_{\text{2}}{\text{O}}_{\left(\text{l}\right)}\text{ΔH°=-5500}\text{kJ/mole}$

The mass of oxygen gas required to support the increase in energy assumption for one decade is calculated below,

$\begin{array}{l}\text{Mass}\text{of}\text{oxygen}\text{=}{\text{100×10}}^{\text{15}}\text{kJ×}\frac{\text{1}\text{mole}{\text{C}}_{\text{8}}{\text{H}}_{\text{18}}}{\text{5500}\text{kJ}}\text{×}\frac{\frac{\text{25}}{\text{2}}\text{mole}{\text{O}}_{\text{2}}}{\text{1}\text{mole}{\text{C}}_{\text{8}}{\text{H}}_{\text{18}}}\text{×}\frac{\text{32}\text{g}{\text{O}}_{\text{2}}}{\text{1}\text{mole}{\text{O}}_{\text{2}}}\\ \text{=}{\text{7×10}}^{\text{15}}\text{g}{\text{O}}_{\text{2}}\end{array}$

The total mass of atmosphere is ${\text{5×10}}^{\text{15}}\text{kg}\text{.}$  Since, the atmosphere is roughly $\text{20\%}{\text{O}}_{\text{2}}$ and $\text{80\%}{\text{N}}_{\text{2}}$ moles of gas, the average mass percent of oxygen in the atmosphere is calculated as,

$\frac{\text{20}\text{mole}{\text{O}}_{\text{2}}\text{×32}\text{g/mole}}{\left(\text{20}\text{mole}{\text{O}}_{\text{2}}\text{×32}\text{g/mole}\right)\text{+}\left(\text{80}\text{mole}{\text{N}}_{\text{2}}\text{×28}\text{g/mole}\right)}\text{×100\%}\text{=}\text{22\%}{\text{O}}_{\text{2}}\text{by}\text{mass}$

Therefore, the mass of oxygen in the atmosphere is calculated below,

${\text{5×10}}^{\text{18}}\text{kg×}\frac{\text{1000}\text{g}}{\text{1}\text{kg}}\text{×0}\text{.22}\text{=}{\text{1×10}}^{\text{21}}{\text{gO}}_{\text{2}}$

Therefore, the percent reduction of oxygen in our atmosphere over one decade is due to the projected increase in the production of energy that would be given as,

$\frac{{\text{7×10}}^{\text{15}}{\text{gO}}_{\text{2}}}{{\text{1×10}}^{\text{21}}{\text{gO}}_{\text{2}}}\text{×100\%}\text{=}\text{0}\text{.0007\%}\text{decrease}{\text{inO}}_{\text{2}}$

Such a small decrease in atmospheric pressure would be insignificant.