
Concept explainers
Find the slope
Answer to Problem 60P
The slope
The deflection
The slope
The slope
The deflection
Explanation of Solution
Given information:
The Young’s modulus (E) is 30,000 ksi.
The moment of inertia of the section AB is (I) is
The moment of inertia of the section BD is (I) is
Calculation:
Consider flexural rigidity EI of the beam is constant.
To draw a
Show the free body diagram of the given beam as in Figure (1).
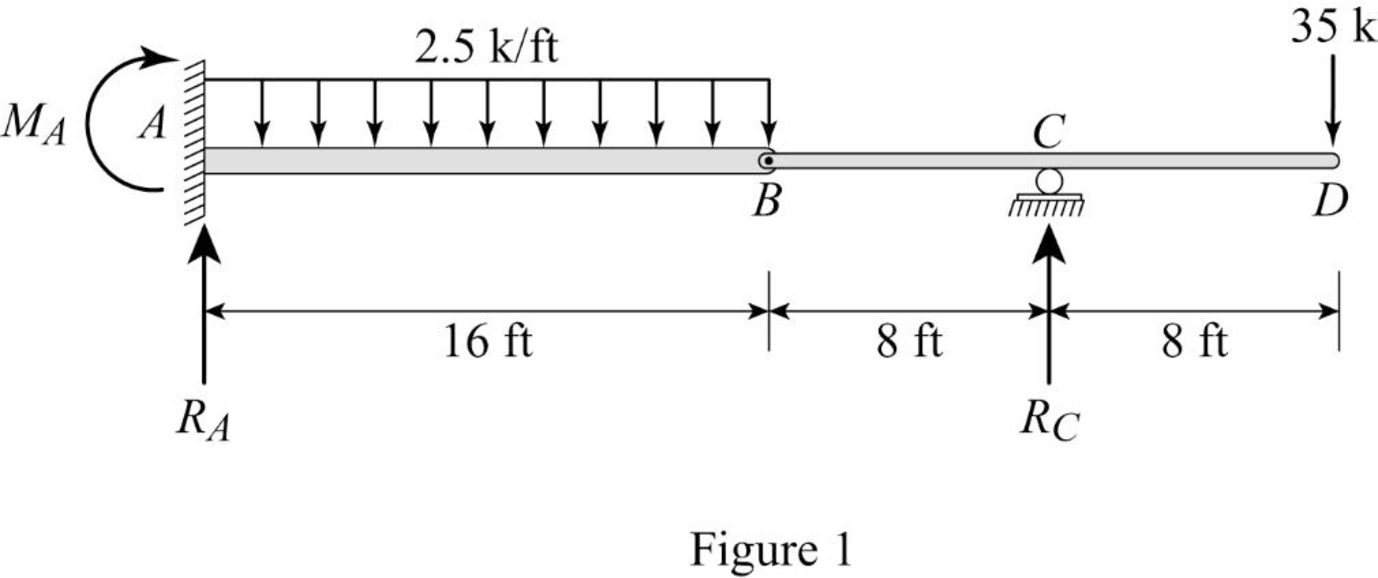
Refer Figure (1),
Consider upward is positive and downward is negative.
Consider clockwise is negative and counterclowise is positive.
Refer Figure (1),
Consider reaction at A and C as
Take moment about point B.
Determine the reaction at D;
Determine the reaction at support A;
Determine the moment at A:
Show the reaction of the given beam as in Figure (2).
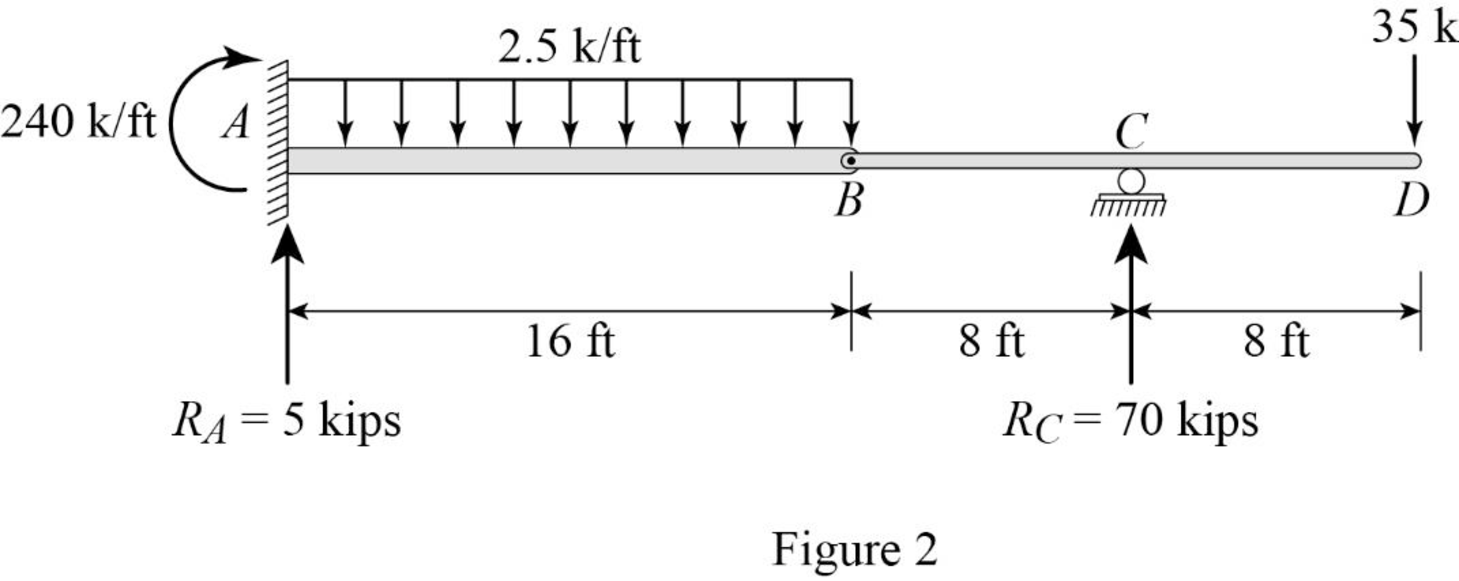
Determine the bending moment at B;
Determine the bending moment at C;
Determine the bending moment at D;
Determine the positive bending moment at A using the relation;
Show the reaction and point load of the beam as in Figure (3).
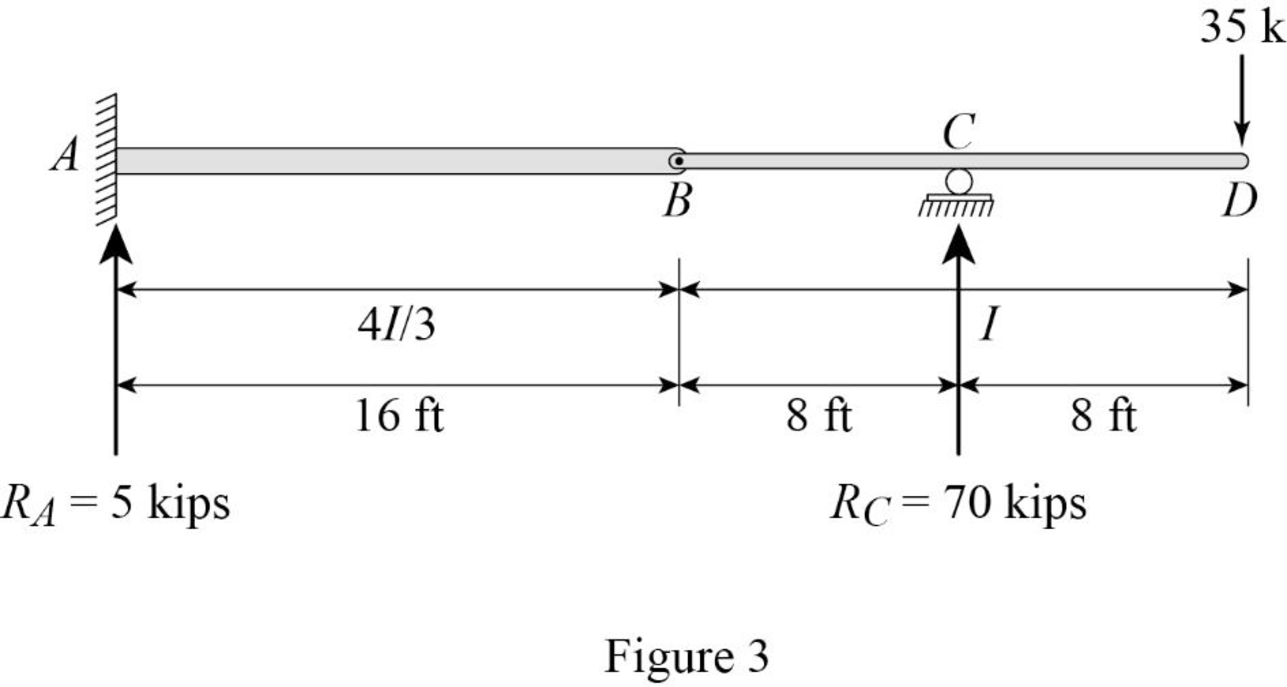
Determine the value of
Substitute
Show the
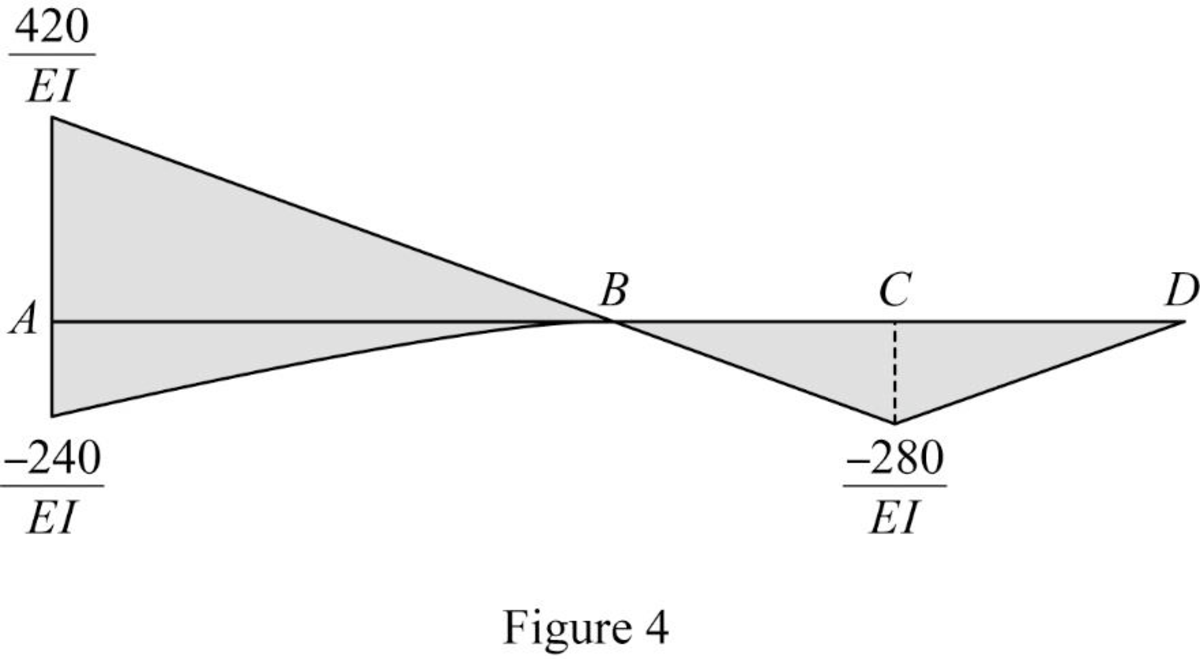
Show the conjugate beam as in Figure (5).
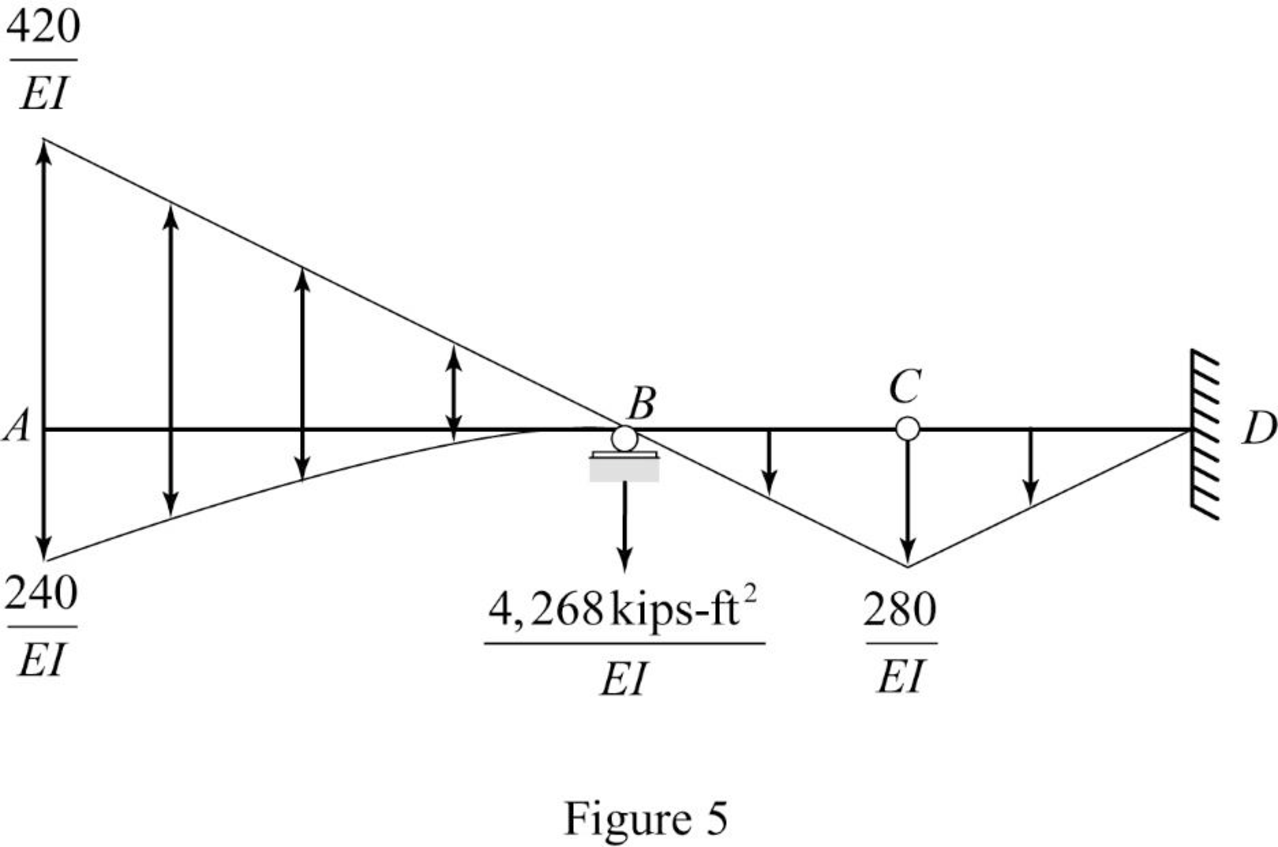
Determine the support reaction at support B;
Determine the shear force at B (left) using the relation;
Substitute 16 ft for
Determine the slope at B (left) using the relation;
Substitute 30,000 ksi for E and
Hence, the slope at B (left) is
Determine the slope at B (right) using the relation;
Substitute
Substitute 30,000 ksi for E and
Hence, the deflection at B (right) is
Determine the bending moment at B using the relation;
Substitute 16 ft for
Determine the deflection at B using the relation;
Substitute 30,000 ksi for E and
Hence, the deflection at B is
Determine the shear force at D using the relation;
Here, b is the width and h is the height of respective triangle and parabola.
Substitute 16 ft for
Determine the slope at D using the relation;
Substitute 30,000 ksi for E and
Hence, the deflection at D is
Determine the bending moment at D using the relation;
Substitute 16 ft for
Determine the deflection at D using the relation;
Substitute 30,000 ksi for E and
Hence, the deflection at D is
Want to see more full solutions like this?
Chapter 6 Solutions
EBK STRUCTURAL ANALYSIS
- 9.16 Two vertical parallel plates are spaced 0.012 ft apart. If the pressure decreases at a rate of 100 psf/ft in the vertical z direction in the fluid between the plates, what is the maximum fluid velocity in the Z direction? The fluid has a viscosity of 10-3 Ibf s/ft² and a specific gravity of 0.80. .arrow_forwardPlease explain steps using software.arrow_forwardPlease explain steps for using softwarearrow_forward
- Design the reinforced masonry beam in the wall shown below. The wall is to be constructed of fully grouted hollow concrete masonry units in running bond. It is to carry its own weight plus a superimposed dead load of 2.5 kips/ft and a live load of 0.8 kip/ft. Determine the width of the masonry units (by trials), and the amounts of the longitudinal and shear reinforcement required using the strength design method of TMS 402-22. Show the layout of the reinforcements with diagrams. Use fm = 2,000 psi, Grade 60(60 ksi) steel, and Type S Portland cement mortar. Assume that the centroid of the bottom rebar is 3 inches from the bottom face of the beam. ( you may assume that the unit weight of fully grouted concrete masonry is 125 lbs per cubic foot.)arrow_forward6. The easiest method to solve the beam shown in question number 14 is A. Force method B. Slope deflection method C. Moment distribution method D. Virtual work method E. Stiffness matrix method 17. The value of 8 caused by applying CW moment at A equal to 18. A. ML/2E1 B. ML/3E1 C. ML/4E1 D. ML/6EI E. None of the above For the beam shown below, the moment at A kN.m CCW. Assume P= 8 kN equals to ........ A. 20 B. 22.5 C. 25 D. 27.5 E. 30 M L A unlocked joint end pin P P P B A 1m 1m 2m 2m 19. The analysis of indeterminate non sway frames using moment distribution method does not need..... A. Finding stiffness factors of members B. Finding fix end moments C. Using compatibility equations D. Removing redundants E. Cand D 0. The frame shown is kinematically 6 kN/m indeterminate to ................ degree. A, C and D are fixed. E and B are pinned. A. First B. Second C. Third D. Fourth E. None of the above 6 m Sm 7 marrow_forward1. The moment at A using slope deflection method equals to 10 kN ..... kN. m CCW. A. 2.5 B. 5 C. 7.5 D. 10 E. None of the above 2m 2m B 10 kN + 2m + 2m 2. To solve the beam shown using slope deflection method,. ...... unknowns (s) 25 kN 15 kN/m should be selected. A. One B. Two fix C. Three D. Four E. None of the above magnitude of the rotation at B for the me shown using slope deflection method quals to El constant. A. -162/EI B. -162 El C. 40/El D. -40 El E. 0.3 radian B A 3 m 3 m -4 m- 4k/ft roller A fix 18 ft. To solve the beam shown using slope deflection method, should be fix selected as equilibrium equation (s). A. MAB+MBA = 0 B. MAB + MBA 0 and MBC=0 C. MBA+MBC = 0 D. MBA+MBC = 0 and MCB=0 E. None of the above B fix fix 9ft 20 kN/m 80 EN pin 9 m 3 m rollerarrow_forward
- Solvearrow_forward5. The number of unknowns for the frame shown using slope deflection method is... Assume A, B and D are fixed and interior hinge at C A. Two B. Four C. Six D. Eight E. None of the above 10 kN B Qc 4m A 3m + + 3m 3m 6. 7. The slope-deflection method was originally developed by Heinrich Manderla and Otto Mohr for the purpose of studying. A. secondary stresses in trusses B. secondary stresses in beams and frames C. Indeterminate beams and frames analysis D. Determinate beams and frames analysis E. None of the above In structures that have non-parallel end members, the displacement of the members will be..... A. Similar B. Different C. Proportional D. Zero E. None of the above. 8. The magnitude of the fix end moment at A 4k/ft using slope deflection method equals to pin exfix ...........k. ft. A. 25 B. -25 C. 40 D. -40 E. None of the above. A roller 15 ft- 12 f The magnitude of MBC for the frame shown in question number 3 using slope deflection method equals Assume El constant for all…arrow_forwardQ2. An isotropic rectangular slab (6 x 8) m is fixed at 3- edges and free at one edge as shown below. The reinforcement provides a positive yield moment of (10) kN.m/m and along the fixed edge a negative yield moment (m) of (14) kN.m/ m. Determine the collapse load if the slab carries a u.d.L. of (w) kN/m² including the slab own weight. W free C Gm fixed 8 m darrow_forward
- Reinforced Concrete Design 4 Second Monthly Exam 15/4/2025 Q1. A double T-concrete beam is prestressed with 2- tendons each of cross-sectional area of (600) mm² as shown below. Determine the allowable service load. Given: Span = 12 m, fse=1400 N/mm², fé= 50 N/mm², Ct = 163 mm, Cb =437 mm, I=7586 x 10 mm*. 10 KN/M * 25.00 x-500x 1500 +500 +100 163 不 -A 500 12m + 437 += 50 1 150 150 600mm 600mmarrow_forward5-18 Determine the maximum service live load that the column shown in Figure P5-18 can support if the live load is twice the dead load. (Lc)x = KxLx = 24 ft, (Lc)y = KyLy = 16 ft = 36 ksi. Solve by LRFD and ASD methods. and Fy Figure P5-18 C6×13 C6×13 PLX14X4arrow_forwardPlease answer the question in the picture, show all of you work in pictures and handwritten.arrow_forward
