
Concept explainers
Find the equations for slope and deflection of the beam using direct integration method.
Answer to Problem 3P
The equation for slope for segment AB is
The equation for deflection for segment AB is
The equation for slope for segment BC is
The equation for deflection for segment BC is
Explanation of Solution
Calculation:
Draw the free body diagram of the beam as in Figure (1).
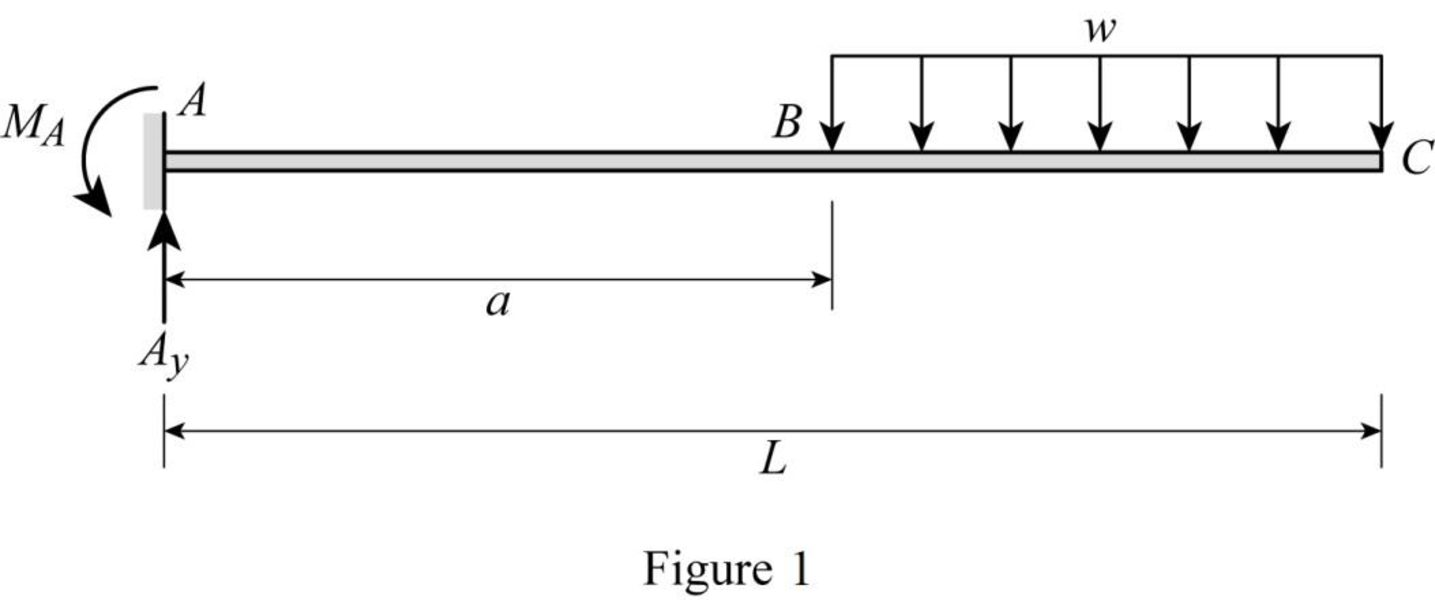
Refer Figure (1),
Find the reaction at support A.
Apply vertical equilibrium along y-axis.
Consider upward force as positive.
Find the moment at A.
Consider anticlockwise moment as positive.
Segment AB:
Consider a section
Sketch the free body diagram when section
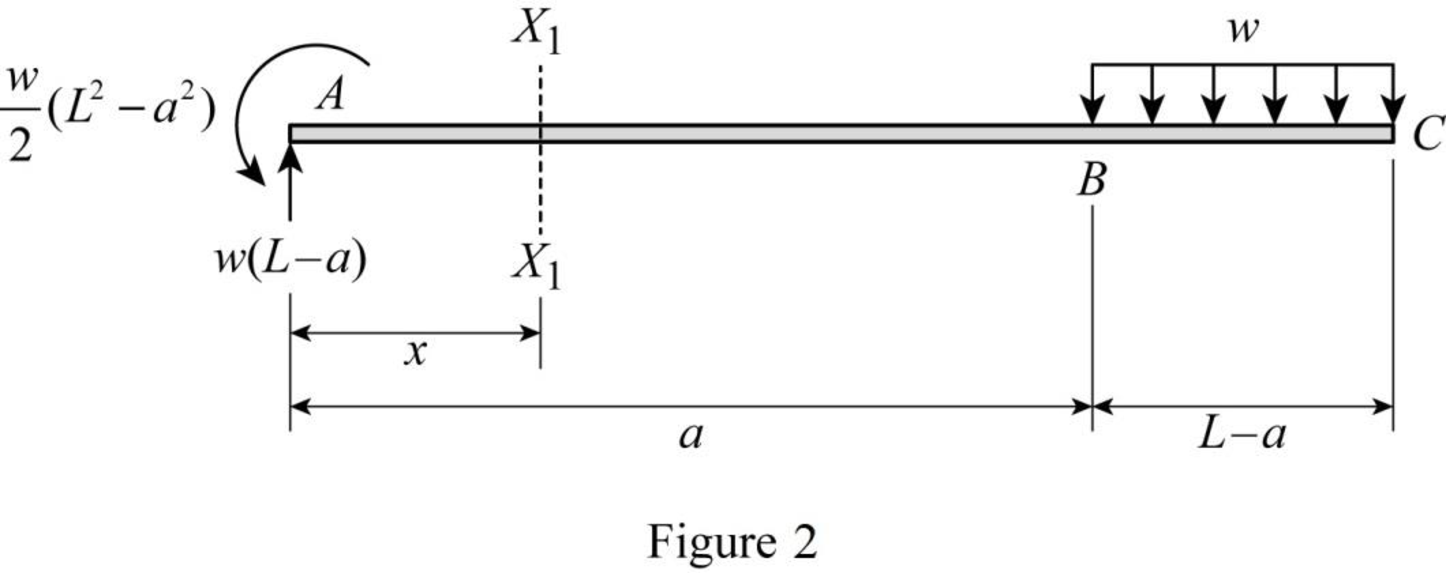
Refer Figure (2),
Take the moment at section
Write the equation for
Find the equation for slope
Integrate Equation (1) with respect to x.
Find the equation for deflection
Integrate again Equation (2) with respect to x.
Find the integration constants
Apply boundary conditions in Equation (2):
At
Apply boundary conditions in Equation (1):
At
Find the equation for slope of segment AB.
Substitute 0 for
Thus, the equation for slope of segment AB is
Find the equation for deflection of segment AB.
Substitute 0 for
Thus, the equation for deflection is
Segment BC:
Consider a section
Sketch the free body diagram when section
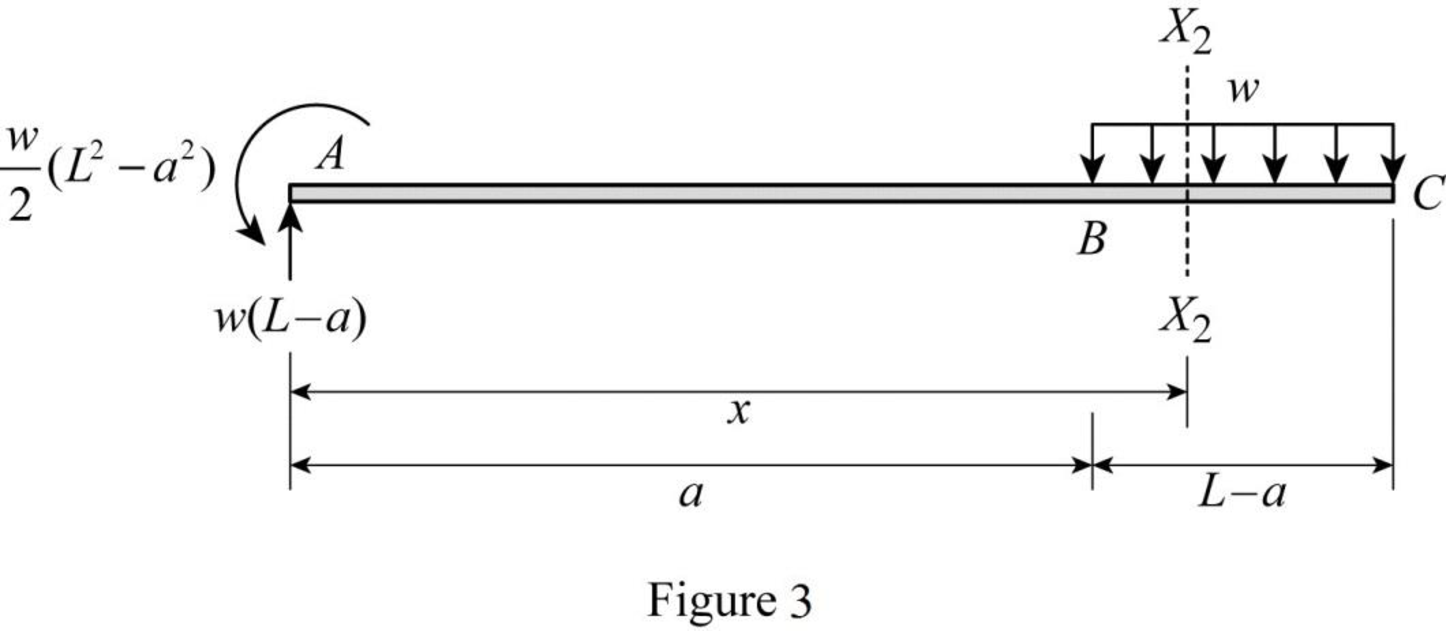
Refer Figure 3.
Write the equation for bending moment at section
Write the equation for
Write the equation for slope.
Integrate Equation (4) with respect to x.
Write the equation for deflection.
Integrate Equation (5) with respect to x.
Find the integration constants
Apply boundary conditions in Equation (3):
At
Apply boundary conditions in Equation (4):
At
Find the equation for slope of segment BC.
Substitute
Thus, the equation for slope of segment BC is
Find the equation for deflection of segment BC.
Substitute
Thus, the equation for deflection of segment BC is
Want to see more full solutions like this?
Chapter 6 Solutions
EBK STRUCTURAL ANALYSIS
- 6-21 Four 3×3× 1/4 angles are used to form the member shown in the accompanying illustration. The member is 24 ft long, has pinned ends, and consists of A572-Grade 50 steel. Determine the LRFD design strength and the ASD allowable strength of the member. Design single lacing and end tie plates, assuming connections are made to the angles with 3/4-in diameter bolts. (Ans. 159.1 k LRFD; 106.0 k ASD) Figure P6-21 12 in L 12 inarrow_forward1000 th 2' 2' w=200 to /ft Handout Problem #3. A beam has the loading and cross section shown. 1) Draw the shear force and bending moment diagrams for the beam. 5" 2) Determine the maximum bending stress in the beam. Carefully identify its location both along the beam and along the cross section. 3) Determine the maximum transverse shear stress in the beam. Carefully identify its location both along the beam and along the cross section: y=2" up from bottom "INA = 33.33 int VMAX = 1160+b MMAX - 2704 Hb-ft QMAX = 8mm³arrow_forwardUnits: lb-ft Handout Problem #2 The dimensions of the shape as well as the bending moment diagram of a flanged wooden shape are shown. Determine: (a) the maximum tensile bending stress at any location along the beam and (b) the maximum compressive bending stress at any location along the beam. 10 in. 10,580 9,200 4,743 2 in. 8 in. 2 in. 2 in. -8,400 6 in.arrow_forward
- (USE 0BC 2024) For a 800 m2 4-storey sprinklered Dry-cleaning establishment (not using explosive solvents), facing 1 street(s), what are the minimum required fire-resistance ratings (FRR) or fire-protection ratings (FPR) for the following? Typical floor assembly (in minutes, please. Just write the number of minutes please) Detailed OBC reference = Public corridor wall (in minutes please) Detailed OBC reference = Suite egress door (in minutes, please) = Detailed OBC reference = Exit stair walls (in minutes, please) = Detailed OBC reference = Exit stair door (in minutes, please) = Detailed OBC reference = Elevator shaft enclosure (in minutes, please) = Detailed OBC reference = Vertical mechanical shaft enclosure (in minutes, please) = Detailed OBC reference =arrow_forwardQuestion 6 options: The fourth storey of this "Dry-cleaning establishment (not using flammable solvents)" building measures 41 m x 19 m and has a public corridor. Determine the following dimensions, in millimetres (mm) The minimum width of its ramp, if it is sloped at 6°. Please give your answer to the nearest millimetre. The minimum width of its egress doors for Suite D (measuring 6 m × 4 m, ignored the elevator). Please give your answer to the nearest millimetre. The minimum width of its corridor. Please give your answer to the nearest millimetre. The minimum width of its ramp, if it is sloped at 13°. Please give your answer to the nearest millimetre.arrow_forwardFor the exposing building face marked (XX) of this unsprinklered 'Beauty parlours' building, please determine the following. justify THE answer in your hand-written solution.arrow_forward
- If the angle for the sloped glazing below is 45°, is it considered part of the roof or part of the wall? justify the answer with appropriate and detailed OBC references.arrow_forwardDetermine the state of stress acting at point E. Show the results on a differential elementat this point.arrow_forwardConsider the structure shown in the following figure, which includes two identical towers, a main cable whose unstretched length is 110 m handing between them, and two side cables with negligible weights (so that they can be modeled as massless springs). The side cables are pretentioned so that the net horizontal force on a tower iszero. The mass per unit length of the main cable is 10 kg/m and EAo = 1000KN. Thehorizontal distance between the two towers is 100 m. The angle del is 60°. By design the total horizontal load on each tower is zero. Find A)The horizontal and vertical loads exerted on each tower by the main cable B)The minimum mass M of the counter weights. Note that the counter weights are blocked from moving in the horizontal directionarrow_forward
- 4th Order Rurka-Kutta Method This assignment will expand your skills on using Excel to perform some numerical analyses and plot your results. It is a means to familiarize you more with basic features in the spreadsheet. Preliminaries: a. Start a new file called R-K.xlsx (for this exercise, you may use the work you did in class but please be careful not to delete what you already have) b. Plan ahead Exercise 1: Using the 4" Order Ruga-Kutta Method that we recently learned, evaluate the following ordinary differential equation (ODE): dx f(t, x) = = x+t² dt At the initial position, X= 0, the time is = 0.1 minutes. Using a step size of, h = 0.05, what is the time spent to reach a position that is equal to 17 (Hint: use a O and b 1) Exercise 2 Using the 4th Order Ruga-Kutta Method, solve the following problem: The concentration of a certain non-reactive (conservative) chemical is given as a function of time by: de f(t,c) = = 30-3c Where c is the concentration and t is time. At the initial…arrow_forwardWhat percentage of all communication is screened out or changed by the receiver?”arrow_forwardIn testing a certain kind or truck tire over rugged terrain, it is found that 20% of the trucks fail to complete the test run without a blowout. Of the next 13 trucks tested, find the probability that (a) from 2 to 6 have blowouts, (b) fewer than 4 have blowouts, and (c) more than 5 have blowouts. Click here to view page 1 of the table of binomial probability sums. Click here to view page 2 of the table of binomial probability sums. (a) The probability that from 2 to 6 trucks have blowouts is (Round to four decimal places as needed.)arrow_forward
