
Concept explainers
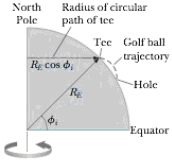
A golfer tees off from a location precisely at ϕi = 35.0° north latitude. He hits the ball due south, with range 285 m. The ball’s initial velocity is at 48.0° above the horizontal. Suppose air resistance is negligible for the golf ball. (a) For how long is the ball in flight? The cup is due south of the golfer’s location, and the golfer would have a hole-in-one if the Earth were not rotating. The Earth’s rotation makes the tee move in a circle of radius RE cos ϕi = (6.37 × 106 m) cos 35.0° as shown in Figure P6.47. The tee completes one revolution each day. (b) Find the eastward speed of the tee relative to the stars. The hole is also moving cast, but it is 285 m farther south and thus at a slightly lower latitude ϕf. Because the hole moves in a slightly larger circle, its speed must he greater than that of the tee. (c) By how much does the hole’s speed exceed that of the tee? During the time interval the ball is in flight, it moves upward and downward as well as southward with the projectile motion you studied in Chapter 4, but it also moves eastward with the speed you found in part (b). The hole moves to the east at a faster speed, however, pulling ahead of the ball with the relative speed you found in part (c). (d) How far to the west of the hole does the ball land?
Figure P6.47
(a)
The time of flight of the ball.
Answer to Problem 47CP
The time for which the ball be in flight is
Explanation of Solution
The range of the motion after hitting the ball is
The range of the parabolic motion
Here,
Write the expression for the equation for parabolic motion
As initial and final distance is equal,
Rearrange the above expression for
Substitute
Rearrange the above expression for
Substitute
Conclusion:
Substitute
Therefore, the time for which the ball be in flight is
(b)
The relative eastward speed of the tee with respect to the stars.
Answer to Problem 47CP
The relative eastward speed of the tee with respect to the stars is
Explanation of Solution
Write the formula to calculate the eastward speed of the tee relative to the stars
Here,
Conclusion:
Substitute
Therefore, the relative eastward speed of the tee with respect to the stars is
(c)
The value by which the hole's speed exceed that of the tee.
Answer to Problem 47CP
The value by which the hole's speed exceed that of the tee is
Explanation of Solution
Write the formula to calculate the length of the arc
Rearrange the above expression for
Substitute
Write the formula to calculate the speed of the hole
Here,
Substitute
Calculate the difference between the speed of tee and the speed of hole.
Here,
Conclusion:
Substitute
Therefore, the value by which the hole's speed exceed that of the tee is
(d)
The distance to the west of the hole from the position where the ball lands.
Answer to Problem 47CP
The distance to the west of the hole from the position where the ball land is
Explanation of Solution
Write the expression for the distance to west of the hole
Here,
Conclusion:
Substitute
Therefore, the distance to the west of the hole from the position where the ball land is
Want to see more full solutions like this?
Chapter 6 Solutions
Physics for Scientists and Engineers
- A thrown brick hits a window, but doesn't break it. Instead it reverses direction and ends down on the ground below the window. Since the brick didn't break the glass, we know: О The force of the brick on the glass > the force of the glass on the brick. О The force of the brick on the glass the force of the glass on the brick. = О The force of the brick on the glass < the force of the glass on the brick. О The brick didn't slow down as it broke the glass.arrow_forwardAlexandra (wearing rubber boots for traction) is attempting to drag her 32.6-kg Golden Retriever across the smooth ice by applying a horizontal force. What force must she apply to move the dog with a constant speed of 0.950 m/s? ☐ 31.0 lb. ☐ 319 kg. ○ Zero. 32.6 kg.arrow_forwardThe figure shows a graph of the acceleration of an object as a function of the net force acting on it. The mass of this object, in grams, is closest to 11 a(m/s²) 8.0+ 6.0- 4.0- 2.0- 0+ F(N) 0.00 0.50 1.00 ☐ 130 ○ 8000 ☐ 89arrow_forward
- Values that are within standard deviations represent measurements that are considered to be near the true value. Review the data from the lab and determine whether your data is within standard deviations. Report, using numerical values, whether your data for each angle is within standard deviations. An acceptable margin of error typically falls between 4% and 8% at the 95% confidence level. Review your data for each angle to determine whether the margin of error is within an acceptable range. Report with numerical values, whether your data for each angle is within an acceptable margin of error. Can you help explain what my data means in terms of the standard deviation and the ME? Thanks!arrow_forwardA sinusoidal wave is propagating along a stretched string that lies along the x-axis. The displacement of the string as a function of time is graphed in (Figure 1) for particles at x = 0 and at x = 0.0900 m. You are told that the two points x = 0 and x = 0.0900 m are within one wavelength of each other. If the wave is moving in the +x-direction, determine the wavelength. If instead the wave is moving in the -x-direction, determine the wavelength. Please show all stepsarrow_forwardYou are designing a two-string instrument with metal strings 35.0 cm long, as shown in (Figure 1). Both strings are under the same tension. String S1 has a mass of 8.30 g and produces the note middle C (frequency 262 Hz ) in its fundamental mode. What should be the tension in the string? What should be the mass of string S2 so that it will produce A-sharp (frequency 466 Hz ) as its fundamental? To extend the range of your instrument, you include a fret located just under the strings but not normally touching them. How far from the upper end should you put this fret so that when you press S1 tightly against it, this string will produce C-sharp (frequency 277 Hz ) in its fundamental? That is, what is x in the figure? If you press S2 against the fret, what frequency of sound will it produce in its fundamental?arrow_forward
- Please solve and answer the problem correctly please. Thank you!!arrow_forwardPlease help explain this. The experiment without the sandpaper had a 5% experimental error, with sandpaper it is 9.4%. Would the explaination be similar to the experiment without sandpaper? Thanks!arrow_forwardA sinusoidal wave with wavelength 0.400 m travels along a string. The maximum transverse speed of a point on the string is 3.00 m/s and the maximum transverse acceleration is 8.10×104m/s2. What is the propagation speed v of the wave? What is the amplitude A of the wave?arrow_forward
 University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning
An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





