
A space probe, initially at rest, undergoes an internal mechanical malfunction and breaks into three pieces. One piece of mass ml = 48.0 kg travels in the positive x-direction at 12.0 m/s, and a second piece of mass m2 = 62.0 kg travels in the xy-plane at an angle of 105° at 15.0 m/s. The third piece has mass m3 = 112 kg. (a) Sketch a diagram of the situation, labeling the different masses and their velocities, (b) Write the general expression for conservation of momentum in the x- and y-directions in terms of m1, m2, m3, v1, v2 and v3 and the sines and cosines of the angles, taking θ to be the unknown angle, (c) Calculate the final x-components of the momenta of m1 and m2. (d) Calculate the final y-components of the momenta of m1 and m2. (e) Substitute the known momentum components into the general equations of momentum for the x- and y-directions, along with the known mass m3. (f) Solve the two momentum equations for v3 cos θ and v3 sin θ, respectively, and use the identity cos2 θ + sin2 θ = 1 to obtain v3. (g) Divide the equation for v3 sin θ by that for v3 cos θ to obtain tan θ, then obtain the angle by taking the inverse tangent of both sides, (h) In general, would three such pieces necessarily have to move in the same plane? Why?
a)
Answer to Problem 46P
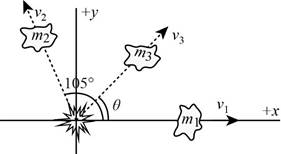
Explanation of Solution
The diagram of the breakage is,
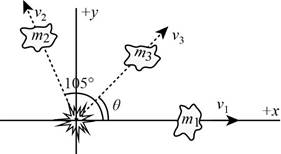
The numerical values of the masses and velocities are,
The numerical values of the masses and velocities are,
Conclusion:
Thus, the diagram of the breakage is,
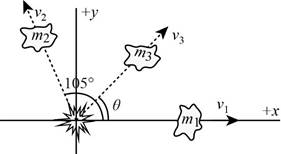
(b)
Answer to Problem 46P
Explanation of Solution
The general expression for the conservation of momentum in x-direction is,
The general expression for the conservation of momentum in y-direction is,
Conclusion:
Thus, the general expression for the conservation of momentum in x-direction is
(c)
Answer to Problem 46P
Explanation of Solution
The final x-component of the momenta of the mass
Substitute
The final x-component of the momenta of the mass
Substitute
Conclusion:
Thus, the final x-component of the momenta of the mass
(d)
Answer to Problem 46P
Explanation of Solution
The final y-component of the momenta of the mass
Substitute
The final y-component of the momenta of the mass
Substitute
Conclusion:
Thus, the final y-component of the momenta of the mass
(e)
Answer to Problem 46P
Explanation of Solution
The final x-component of the momenta of mass
The final y-component of the momenta of mass
Conclusion:
Thus, the final x and y-components of the momenta of mass
(f)
Answer to Problem 46P
Explanation of Solution
In the x-direction,
In the y-direction,
Squaring and adding the equations,
Conclusion:
Thus, the velocity
(g)
Answer to Problem 46P
Explanation of Solution
The tangent of the angle is,
Thus, the angle is,
The angle must be in third quadrant. So, angle
Conclusion:
Thus, the angle
(h)
Answer to Problem 46P
Explanation of Solution
The momentum of the third fragment must be equal in magnitude and must be in the opposite direction to the resultant of the other two fragments momenta. So, all three pieces have to move in the same plane.
Conclusion:
Thus, all three pieces have to move in the same plane.
Want to see more full solutions like this?
Chapter 6 Solutions
Bundle: College Physics, Loose-Leaf Version, 11th + WebAssign Printed Access Card for Serway/Vuille's College Physics, 11th Edition, Single-Term
Additional Science Textbook Solutions
Fundamentals Of Physics - Volume 1 Only
Essential University Physics (3rd Edition)
College Physics
EBK FUNDAMENTALS OF THERMODYNAMICS, ENH
Glencoe Physics: Principles and Problems, Student Edition
Physical Universe
- A rocket has total mass Mi = 360 kg, including Mfuel = 330 kg of fuel and oxidizer. In interstellar space, it starts from rest at the position x = 0, turns on its engine at time t = 0, and puts out exhaust with relative speed ve = 1 500 m/s at the constant rate k = 2.50 kg/s. The fuel will last for a burn time of Tb = Mfuel/k = 330 kg/(2.5 kg/s) = 132 s. (a) Show that during the burn the velocity of the rocket as a function of time is given by v(t)=veln(1ktMi) (b) Make a graph of the velocity of the rocket as a function of time for times running from 0 to 132 s. (c) Show that the acceleration of the rocket is a(t)=kveMikt (d) Graph the acceleration as a function of time. (c) Show that the position of the rocket is x(t)=ve(Mikt)ln(1ktMi)+vet (f) Graph the position during the burn as a function of time.arrow_forwardA girl of mass mg is standing on a plank of mass mp. Both are originally at rest on a frozen lake that constitutes a frictionless, flat surface. The girl begins to walk along the plank at a constant velocity vgp to the right relative to the plank. (The subscript gp denotes the girl relative to plank.) (a) What is the velocity vpi of the plank relative to the surface of the ice? (b) What is the girls velocity vgi relative to the ice surface?arrow_forwardAn astronaut out on a spacewalk to construct a new section of the International Space Station walks with a constant velocity of 2.00 m/s on a flat sheet of metal placed on a flat, frictionless, horizontal honeycomb surface linking the two parts of the station. The mass of the astronaut is 75.0 kg, and the mass of the sheet of metal is 245 kg. a. What is the velocity of the metal sheet relative to the honeycomb surface? b. What is the speed of the astronaut relative to the honeycomb surface?arrow_forward
- From what might be a possible scene in the comic book The X-Men, the Juggernaut (mJ) is charging into Colossus (mC) and the two collide. The initial speed of the Juggernaut is vJi and the initial speed of Colossus is vCi. After the collision, the final speed of the Juggernaut is vJf and the final speed of Colossus is vCf as they each bounce off of the other, heading in opposite directions. a. What is the impulse experienced by the Juggernaut? b. What is the impulse experienced by Colossus? c. In your own words, explain how these impulses must compare with each other and how they are related to the average force each superhero experiences during the collision.arrow_forwardA particle of mass m moving along the x-axis with a velocity component +u collides head-on and sticks to a particle of mass m/3 moving along the x-axis with the velocity component −u. What is the mass M of the resulting particle?arrow_forwardA 250-kg flatcar 23 m long is moving with a speed of 7.0 m/s along horizontal frictionless rails. A 95-kg worker starts walking from one end of the car to the other in the direction of motion, with a speed of 3.0 m/s with respect to the car. In the time it takes for him to reach the other end, how far has the flatcar moved?arrow_forward
- A man holding a rock sits on a sled that is sliding across a frozen lake (negligible friction) with a speed of 0.530 m/s. The total mass of the sled, man, and rock is 94.5 kg. The mass of the rock is 0.250 kg and the man can throw it with a speed of 14.5 m/s. Both speeds are relative to the ground. Determine the speed of the sled (in m/s) if the man throws the rock forward (i.e., in the direction the sled is moving). m/s Determine the speed of the sled (in m/s) if the man throws the rock directly backward.arrow_forwardA BB gun is fired at a cardboard box of mass m2 = 0.75 kg on a frictionless surface. The BB has a mass of m1 = 0.0165 kg and travels at a velocity of v1 = 91 m/s. It is observed that the box is moving at a velocity of v2 = 0.17 m/s after the BB passes through it. (a) Write an expression for the magnitude of the BB's velocity as it exits the box vf. vf = v1 - m2/m1 v2 ✔ Correct! (b) What is the BB's final velocity vf, in meters per second? vf = | (c) If the BB doesn't exit the box, what will the velocity of the box v'2, be in meters per second? ***Please explain how to derive the equation (the answer to part a).arrow_forwardyou have to use one of these equations p = mv Ft = Δp Δp=m(vf-vi) m1v1i + m2v2i = m1v1f + m2v2f m1v1i + m2v2i = m(1+2)vfarrow_forward
- A system of three particles with masses m1 = 3.0 kg, m2 = 4.0 kg and m3 = 8.0 kg is placed on a two dimensional xy plane. The scales on the axes are set by x, = 2.0 m and y, = 2.0 m. y (m) mg m1 * (m) Figure 2 (a) Find out the x coordinate of the system's center of mass. (b) Find out the y coordinate of the system's center of mass. (c) Find out the acceleration of the system if an external force of 5 N acts on it.arrow_forwardFor a safe reentry into Earth's atmosphere, the pilots of a space capsule must reduce their speed from 2.60 x 104 m/s to 1.10 × 104 m/s. The rocket engine produces a backward force on the capsule of 1.80 x 105 N. The mass of the capsule is 3280 kg. For how long must they fire their engine? Ignore the change in mass of the capsule due to the expulsion of exhaust gases.arrow_forwardConsider a system of two particles in the xy-plane. For the first particle, Its mass is m₁ = 1.30 kg Its position is 7¹₁ = (1.202 + 2.203) m Its velocity is ₁ = (2.2002 + 0.100)) m/s For the second particle, Its mass is m₂ = 2.90 kg Its position is 7¹2 = (-3.60% - 2.403) m Its velocity is v₂ = (2.2001 - 2.000)) m/s a. Find the position of the center of mass of the system. 7CM = im+m b. Determine the velocity of the center of mass. UCM = 2 m/s + m/s c. What is the total linear momentum of the system? Pr = kg-m/s + kg-m/sarrow_forward
 College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning





