7th Edition

ISBN: 9780134684291

Author: Larson

Publisher: PEARSON CO

See similar textbooks

Videos

Textbook Question

Chapter 6, Problem 2RSRD

The Safe Drinking Water Act, which was passed in 1974, allows the Environmental Protection Agency (EPA) to regulate the levels of contaminants in drinking water. The EPA requires that water utilities give their customers water quality reports annually. These reports include the results of daily water quality monitoring, which is performed to determine whether drinking water is safe for consumption.

A water department tests for contaminants at water treatment plants and at customers laps. These contaminants include microorganisms, organic chemicals, and inorganic chemicals such as cyanide. Cyanide’s presence in drinking water is the result of discharges from Steel, plastics, and fertilizer factories. For drinking water, the maximum contaminant level of cyanide is 0.2 part per million.

As part of your job for your city’s water department, you are preparing a report that includes an analysis of the results shown in the figure at the right. The figure shows the point estimates for the population mean concentration and the 95% confidence intervals for μ for cyanide over a three-year period. The data are based on random water samples taken by the city’s three water treatment plants.

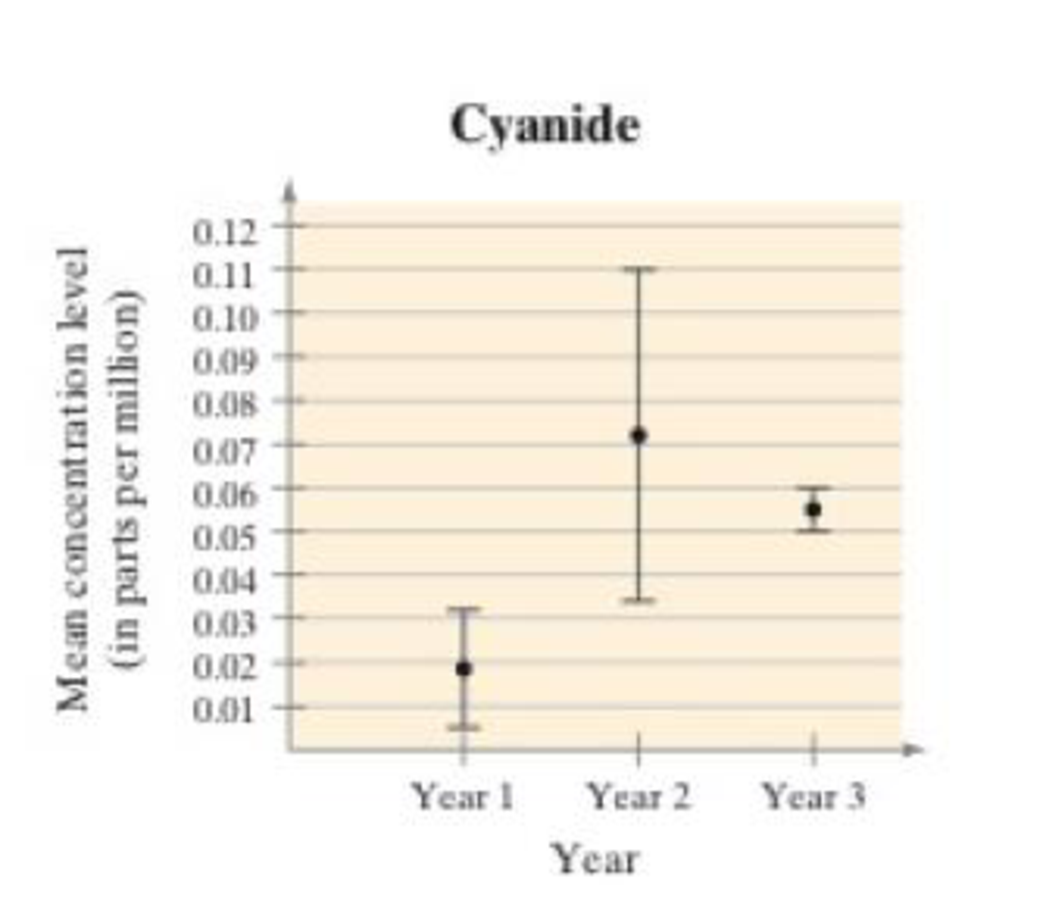
Chapter 6, Problem 2RSRD, The Safe Drinking Water Act, which was passed in 1974, allows the Environmental Protection Agency

2. What Can You Conclude?

Using the results of Exercise 1, what can you conclude about the concentrations of cyanide in the drinking water?

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 6, Problem 1RSRD

Chapter 6, Problem 3RSRD

Students have asked these similar questions

Introduce yourself and describe a time when you used data in a personal or professional decision. This could be anything from analyzing sales data on the job to making an informed purchasing decision about a home or car. Describe to Susan how to take a sample of the student population that would not represent the population well. Describe to Susan how to take a sample of the student population that would represent the population well. Finally, describe the relationship of a sample to a population and classify your two samples as random, systematic, cluster, stratified, or convenience.

1.2.17. (!) Let G,, be the graph whose vertices are the permutations of (1,..., n}, with two permutations a₁, ..., a,, and b₁, ..., b, adjacent if they differ by interchanging a pair of adjacent entries (G3 shown below). Prove that G,, is connected. 132 123 213 312 321 231

You are planning an experiment to determine the effect of the brand of gasoline and the weight of a car on gas mileage measured in miles per gallon. You will use a single test car, adding weights so that its total weight is 3000, 3500, or 4000 pounds. The car will drive on a test track at each weight using each of Amoco, Marathon, and Speedway gasoline. Which is the best way to organize the study? Start with 3000 pounds and Amoco and run the car on the test track. Then do 3500 and 4000 pounds. Change to Marathon and go through the three weights in order. Then change to Speedway and do the three weights in order once more. Start with 3000 pounds and Amoco and run the car on the test track. Then change to Marathon and then to Speedway without changing the weight. Then add weights to get 3500 pounds and go through the three gasolines in the same order.Then change to 4000 pounds and do the three gasolines in order again. Choose a gasoline at random, and run the car with this gasoline at…

Chapter 6 Solutions

EBK ELEMENTARY STATISTICS

Ch. 6.1 - In Example 1, the researcher selects a second...Ch. 6.1 - Use the data in Try It Yourself 1 and a 95%...Ch. 6.1 - Use the data in Try It Yourself 1 to construct a...Ch. 6.1 - Use the data in Example 1 and technology to...Ch. 6.1 - Construct a 90% confidence interval for the...Ch. 6.1 - In Example 6, how many student-athletes must the...Ch. 6.1 - When estimating a population mean, are you more...Ch. 6.1 - Which statistic is the best unbiased estimator for...Ch. 6.1 - For the same sample statistics, which level of...Ch. 6.1 - You construct a 95% confidence interval for a...

Knowledge Booster

$Statistics$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.

Solution Summary: The author concludes that the confidence interval for Year 2 is much larger than the other years.

Videos

Want to see the full answer?

Chapter 6 Solutions