Chapter 6, Problem 1P

(a)

To determine

Find the expression of the voltage across an inductor $t>0\text{ s}$.

Answer to Problem 1P

The expression of the voltage across an inductor $t>0\text{ s}$ is $\underset{\_}{0.9e^{-10t}\left(1-10t\right)\text{ mV}}$ for $t>0$.

Explanation of Solution

Given data:

The current through an inductor is $i_L=18t{e}^{-10t}\text{ A}$ for $t\ge 0\text{ s}$.

The inductor value is,

$L=50\mu \text{H}$

Formula used:

Write the general expression to find the voltage across an inductor as,

$v=L\frac{d{i}_L}{dt}$        (1)

Here,

L is the value of inductance of the inductor,

$i_L$ is the current through an inductor, and

$dt$ is the change in time.

Calculation:

Substitute $50\mu \text{H}$ for L and $18t{e}^{-10t}\text{ A}$ for $i_L$ in equation (1) to find voltage across an inductor.

$\begin{array}{l}v=\left(5\times {10}^{-6}\text{ H}\right)\frac{d}{dt}\left(18t{e}^{-10t}\text{ A}\right)\\ v=\left(5\times {10}^{-6}\times 18\right)\left(\left(-10\right)t{e}^{-10t}\text{+}{e}^{-10t}\right)\left\{\because \frac{d}{dt}\left(uv\right)=u\frac{d}{dt}\left(v\right)+v\frac{d}{dt}\left(u\right)\right\}\\ v=0.0009\left(e^{-10t}-10t{e}^{-10t}\right)\text{ V}\end{array}$

$v=0.9e^{-10t}\left(1-10t\right)\text{ mV for }t>0$

Conclusion:

Thus, the expression of the voltage across an inductor $t>0\text{ s}$ is $\underset{\_}{0.9e^{-10t}\left(1-10t\right)\text{ mV}}$ for $t>0$.

(b)

To determine

Calculate the power at the inductor terminals at time of $t=200\mu \text{s}$.

Answer to Problem 1P

The power at the inductor terminals at time of $t=200\mu \text{s}$ is $\underset{\_}{-59.34\mu \text{W}}$.

Explanation of Solution

Calculation:

Given that $i_L=18t{e}^{-10t}\text{ A}$ for $t\ge 0\text{ s}$. The values of current for several instant of times are,

At time $t=0\text{ s}$:

$\begin{array}{l}{i}_L=18\left(0\right)e^{-10\left(0\right)}\text{ A}\\ i_L=0\text{ A}\end{array}$

At time $t=0.05\text{ s}$:

$\begin{array}{l}{i}_L=18\left(0.05\right)e^{-10\left(0.05\right)}\text{ A}\\ i_L=\text{0}\text{.545877 A}\\ i_L=\text{0}\text{.6 A}\end{array}$

At time $t=0.1\text{ s}$:

$\begin{array}{l}{i}_L=18\left(0.01\right)e^{-10\left(0.01\right)}\text{ A}\\ i_L=\text{0}\text{.66218299 A}\\ i_L\cong \text{0}\text{.6622 A}\end{array}$

At time $t=0.15\text{ s}$:

$\begin{array}{l}{i}_L=18\left(0.15\right)e^{-10\left(0.15\right)}\text{ A}\\ i_L=\text{0}\text{.602451 A}\\ i_L\cong \text{0}\text{.61 A}\end{array}$

At time $t=0.2\text{ s}$:

$\begin{array}{l}{i}_L=18\left(0.2\right)e^{-10\left(0.2\right)}\text{ A}\\ i_L=\text{0}\text{.487207019 A}\\ i_L\cong \text{0}\text{.487207 A}\end{array}$

Calculate the voltage at $t=200\text{ms}$.

$\begin{array}{l}v=0.9e^{-10\left(200\times {10}^{-3}\right)}\left(1-10\left(200\times {10}^{-3}\right)\right)\text{ mV}\\ v=0.9e^{-2}\left(1-2\right)\text{ mV}\\ v=-121.8\times {10}^{-3}\text{ mV}\end{array}$

$v=-121.8\mu \text{V}$

Write the formula to find the power in an inductor at $t=200\text{ms}$ as,

$p\left(200\text{ ms}\right)=v\left(200\text{ ms}\right)i_L\left(200\text{ ms}\right)$

Substitute $-121.8\mu \text{V}$ for $v\left(200\text{ ms}\right)$ and $\text{0}\text{.487207 A}$ for $i_L\left(200\text{ ms}\right)$ in above equation.

$\begin{array}{l}p\left(200\text{ ms}\right)=\left(-121.8\mu \text{V}\right)\left(\text{0}\text{.487207 A}\right)\\ p\left(200\text{ ms}\right)=\left(-121.8\times \text{0}\text{.487207 A}\right)\mu \text{V}\cdot \text{A}\end{array}$

$p\left(200\text{ ms}\right)=-59.34\mu \text{W}$

PSpice simulation:

Use all the above calculated values to give as an input to the PSpice simulation.

From the given information, the current passing through an inductor and here a small resistor is connected in series with inductor to avoid the simulation error.

Draw the circuit as shown in below Figure 1.

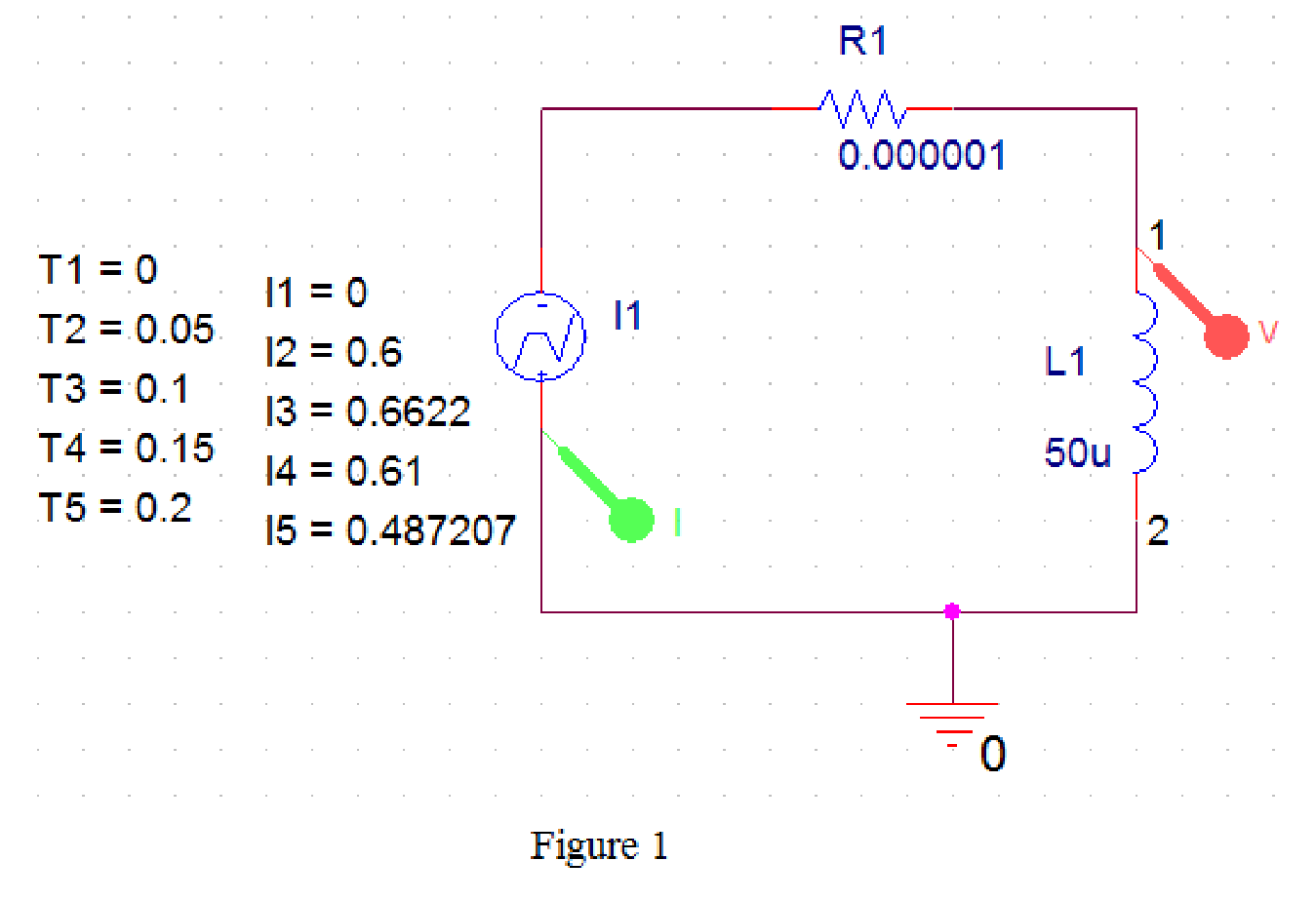
Provide the simulation settings as shown in below Figure 2.

Now, save and run the simulation, then the plot for the input current and voltage across an inductor will be displays as shown in Figure 3.

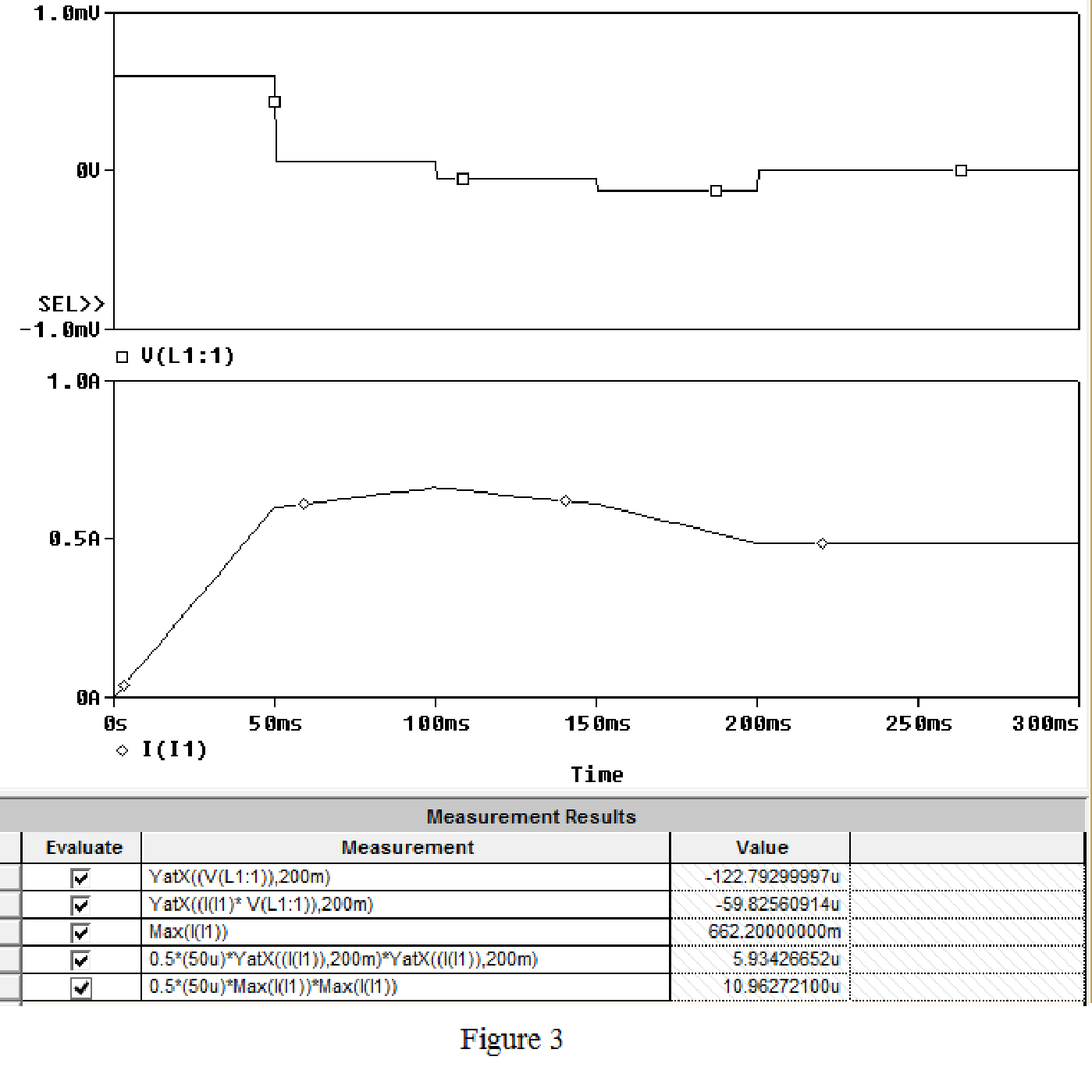
From the Figure 3, the first function is used to read the voltage at $t=200\text{ ms}$, which is shown as $v=-127.79299\mu \text{V}$. The second function is used to calculate the power at $t=200\text{ ms}$ which is showing as,

$\begin{array}{l}p=-59.825\mu \text{W}\\ p\cong -59.83\mu \text{W}\end{array}$

The power calculated at $t=200\text{ ms}$ theoretically and with simulation, both are approximately equal.

Conclusion:

Thus, the power at the inductor terminals at time of $t=200\mu \text{s}$ is $\underset{\_}{-59.34\mu \text{W}}$.

(c)

To determine

Check whether an inductor is delivering the power or absorbing the power.

Answer to Problem 1P

An inductor is delivering the power.

Explanation of Solution

Discussion:

The power calculated in an inductor has the negative sign which indicates that the power is delivering by an inductor.

Conclusion:

Thus, an inductor is delivering the power.

(d)

To determine

Calculate the energy stored in an inductor in micro joules at $t=200\text{ ms}$.

Answer to Problem 1P

The energy stored in an inductor in at $t=200\text{ ms}$ is $\underset{\_}{5.93\mu \text{J}}$.

Explanation of Solution

Discussion:

From the simulation results shown in Part (b), the fourth equation is written to calculate energy stored in an inductor. From the Figure 3, the energy stored in an inductor in at $t=200\text{ ms}$ is $5.93\mu \text{J}$.

Conclusion:

Thus, the energy stored in an inductor in at $t=200\text{ ms}$ is $\underset{\_}{5.93\mu \text{J}}$.

(e)

To determine

Find the maximum energy, and also find the instant of time that occurs.

Answer to Problem 1P

The maximum energy is $\underset{\_}{10.96\mu \text{J}}$, and it occurs at the instant of time $\underset{\_}{t=200\text{ ms}}$.

Explanation of Solution

Discussion:

When the current is maximum energy in an inductor also maximum, since the square of current is directly proportional to the energy stored.

From the Figure 3, it is calculated that maximum current as 662.2 mA, that occurs at $t=200\mu \text{s}$. In Figure 3, the last formula is used to get the maximum energy stored in an inductor in at $t=200\text{ ms}$ is shown as $10.96\mu \text{J}$.

Conclusion:

Thus, the maximum energy is $\underset{\_}{10.96\mu \text{J}}$, and it occurs at the instant of time $\underset{\_}{t=200\text{ ms}}$.