Chapter 6, Problem 16QP

Summary Introduction

To determine: The percentage change in bond price

Introduction:

A bond refers to the debt securities issued by the governments or corporations for raising capital. The borrower does not return the face value until maturity. However, the investor receives the coupons every year until the date of maturity.

Bond price or bond value refers to the present value of the future cash inflows of the bond after discounting at the required rate of return.

Answer to Problem 16QP

The percentage change in bond price is as follows:

Yield to maturity	Bond B	Bond T
5%	5.508%	25.103%
9%	(5.158%)	(18.40%)

The interest rate risk is high for a bond with longer maturity, and the interest rate risk is low for a bond with shorter maturity period. The maturity period of Bond B is 3 years, and the maturity period of Bond T is 20 years. Hence, the Bond T’s bond price fluctuates higher than the bond price of Bond B due to longer maturity.

Explanation of Solution

Given information:

There are two bonds namely Bond B and Bond T. The coupon rate of both the bonds is 7 percent. The bonds pay the coupons semiannually. The price of the bond is equal to its par value. Assume that the par value of both the bonds is $1,000. Bond B will mature in 3 years, and Bond T will mature in 20 years.

Formula:

The formula to calculate the bond value:

$\text{Bond value}=C\times \frac{\left[1-\frac{1}{{\left(1+r\right)}^t}\right]}{r}+\frac{F}{{\left(1+r\right)}^t}$

Where,

“C” refers to the coupon paid per period

“F” refers to the face value paid at maturity

“r” refers to the yield to maturity

“t” refers to the periods to maturity

The formula to calculate the percentage change in price:

$\text{Percentage change in price}=\frac{\text{New price}-\text{Initial price}}{\text{Initial price}}\times 100$

Determine the current price of Bond B:

Bond B is selling at par. It means that the bond value is equivalent to the face value. It also indicates that the coupon rate of the bond is equivalent to the yield to maturity of the bond. As the par value is $1,000, the bond value or bond price of Bond B will be $1,000.

Hence, the current price of Bond B is $1,000.

Determine the current yield to maturity on Bond B:

As the bond is selling at its face value, the coupon rate will be equal to the yield to maturity of the bond. The coupon rate of Bond B is 7 percent.

Hence, the yield to maturity of Bond B is 7 percent.

Determine the current price of Bond T:

Bond T is selling at par. It means that the bond value is equal to the face value. It also indicates that the coupon rate of the bond is equal to the yield to maturity of the bond. As the par value is $1,000, the bond value or bond price of Bond T will be $1,000.

Hence, the current price of Bond T is $1,000.

Determine the current yield to maturity on Bond T:

As the bond is selling at its face value, the coupon rate will be equal to the yield to maturity of the bond. The coupon rate of Bond T is 7 percent.

Hence, the yield to maturity of Bond T is 7 percent.

The percentage change in the bond value of Bond B and Bond T when the interest rates rise by 2 percent:

Compute the new interest rate (yield to maturity) when the interest rates rise:

The interest rate refers to the yield to maturity of the bond. The initial yield to maturity of the bonds is 7 percent. If the interest rates increases by 2 percent, then the new interest rate or yield to maturity will be 9 percent $(7\text{ percent}+2\text{ percent})$.

Compute the bond value when the yield to maturity of Bond B rises to 9 percent:

The coupon rate of Bond B is 7 percent, and its face value is $1,000. Hence, the annual coupon payment is $70 $(\$1,000\times 7\%)$. As the coupon payments are semiannual, the semiannual coupon payment is $35 $(\$70÷2)$.

The yield to maturity is 9 percent. As the calculations are semiannual, the yield to maturity should also be semiannual. Hence, the semiannual yield to maturity is 4.5 percent $(9\%÷2)$.

The remaining time to maturity is 3 years. As the coupon payment is semiannual, the semiannual periods to maturity are 6 $(3\text{ years}\times 2)$. In other words, “t” equals to 6 6-month or semiannual periods.

$\begin{array}{c}\text{Bond value}=C\times \frac{\left[1-\frac{1}{{\left(1+r\right)}^t}\right]}{r}+\frac{F}{{\left(1+r\right)}^t}\\ =\$35\times \frac{\left[1-\frac{1}{{\left(1+0.045\right)}^6}\right]}{0.045}+\frac{\$1,000}{{\left(1+0.045\right)}^6}\\ =\$180.5255+\$767.8957\\ =\$948.4212\end{array}$

Hence, the bond price of Bond B will be $948.42 when the interest rises to 9 percent.

Compute the percentage change in the price of Bond B when the interest rates rise to 9 percent:

The new price after the increase in interest rate is $948.42. The initial price of the bond was $1,000.

$\begin{array}{c}\text{Percentage change in price}=\frac{\text{New price}-\text{Initial price}}{\text{Initial price}}\times 100\\ =\frac{\$948.42-\$1,000}{\$1,000}\times 100\\ =\frac{\left(\$51.42\right)}{\$1,000}\times 100\\ =\left(5.158\%\right)\end{array}$

Hence, the percentage decrease in the price of Bond B is (5.158 percent) when the interest rates rise to 9 percent.

Compute the bond value when the yield to maturity of Bond T rises to 9 percent:

The coupon rate of Bond T is 7 percent, and its face value is $1,000. Hence, the annual coupon payment is $70 $(\$1,000\times 7\%)$. As the coupon payments are semiannual, the semiannual coupon payment is $35 $(\$70÷2)$.

The yield to maturity is 9 percent. As the calculations are semiannual, the yield to maturity should also be semiannual. Hence, the semiannual yield to maturity is 4.5 percent $(9\%÷2)$.

The remaining time to maturity is 20 years. As the coupon payment is semiannual, the semiannual periods to maturity are 40 $(20\text{ years}\times 2)$. In other words, “t” equals to 40 6-month or semiannual periods.

$\begin{array}{c}\text{Bond value}=C\times \frac{\left[1-\frac{1}{{\left(1+r\right)}^t}\right]}{r}+\frac{F}{{\left(1+r\right)}^t}\\ =\$35\times \frac{\left[1-\frac{1}{{\left(1+0.045\right)}^{40}}\right]}{0.045}+\frac{\$1,000}{{\left(1+0.045\right)}^{40}}\\ =\$644.0554+\$171.9287\\ =\$815.9841\end{array}$

Hence, the bond price of Bond T will be $815.9841 when the interest rises to 9 percent.

Compute the percentage change in the price of Bond T when the interest rates rise to 9 percent:

The new price after the increase in interest rate is $815.9841. The initial price of the bond was $1,000.

$\begin{array}{c}\text{Percentage change in price}=\frac{\text{New price}-\text{Initial price}}{\text{Initial price}}\times 100\\ =\frac{\$815.9841-\$1,000}{\$1,000}\times 100\\ =\frac{\left(\$184.0159\right)}{\$1,000}\times 100\\ =\left(18.40\%\right)\end{array}$

Hence, the percentage decrease in the price of Bond T is (18.40 percent) when the interest rates rise to 9 percent.

The percentage change in the bond value of Bond B and Bond T when the interest rates decline by 2 percent:

Compute the new interest rate (yield to maturity) when the interest rates decline:

The interest rate refers to the yield to maturity of the bond. The initial yield to maturity of the bonds is 5 percent. If the interest rates decline by 2 percent, then the new interest rate or yield to maturity will be 5 percent $(7\text{ percent}-2\text{ percent})$.

Compute the bond value when the yield to maturity of Bond B declines to 5 percent:

The coupon rate of Bond T is 7 percent, and its face value is $1,000. Hence, the annual coupon payment is $70 $(\$1,000\times 7\%)$. As the coupon payments are semiannual, the semiannual coupon payment is $35 $(\$70÷2)$.

The yield to maturity is 5 percent. As the calculations are semiannual, the yield to maturity should also be semiannual. Hence, the semiannual yield to maturity is 2.5 percent $(5\%÷2)$.

The remaining time to maturity is 3 years. As the coupon payment is semiannual, the semiannual periods to maturity are 6 $(3\text{ years}\times 2)$. In other words, “t” equals to 6 6-month or semiannual periods.

$\begin{array}{c}\text{Bond value}=C\times \frac{\left[1-\frac{1}{{\left(1+r\right)}^t}\right]}{r}+\frac{F}{{\left(1+r\right)}^t}\\ =\$35\times \frac{\left[1-\frac{1}{{\left(1+0.025\right)}^6}\right]}{0.025}+\frac{\$1,000}{{\left(1+0.025\right)}^6}\\ =\$192.7844+\$862.2969\\ =\$1,055.08\end{array}$

Hence, the bond price of Bond B will be $1,055.08 when the interest declines to 5 percent.

Compute the percentage change in the price of Bond B when the interest rates decline to 5 percent:

The new price after the increase in interest rate is $1,055.08. The initial price of the bond was $1,000.

$\begin{array}{c}\text{Percentage change in price}=\frac{\text{New price}-\text{Initial price}}{\text{Initial price}}\times 100\\ =\frac{\$1,055.08-\$1,000}{\$1,000}\times 100\\ =\frac{\$55.08}{\$1,000}\times 100\\ =5.508\%\end{array}$

Hence, the percentage increase in the price of Bond B is 5.508 percent when the interest rates decline to 5 percent.

Compute the bond value when the yield to maturity of Bond T declines to 5 percent:

The coupon rate of Bond T is 7 percent, and its face value is $1,000. Hence, the annual coupon payment is $70 $(\$1,000\times 7\%)$. As the coupon payments are semiannual, the semiannual coupon payment is $35 $(\$70÷2)$.

The yield to maturity is 5 percent. As the calculations are semiannual, the yield to maturity should also be semiannual. Hence, the semiannual yield to maturity is 2.5 percent $(5\%÷2)$.

The remaining time to maturity is 20 years. As the coupon payment is semiannual, the semiannual periods to maturity are 40 $(20\text{ years}\times 2)$. In other words, “t” equals to 50 6-month or semiannual periods.

$\begin{array}{c}\text{Bond value}=C\times \frac{\left[1-\frac{1}{{\left(1+r\right)}^t}\right]}{r}+\frac{F}{{\left(1+r\right)}^t}\\ =\$35\times \frac{\left[1-\frac{1}{{\left(1+0.025\right)}^{40}}\right]}{0.025}+\frac{\$1,000}{{\left(1+0.025\right)}^{40}}\\ =\$878.5971+\$372.4306\\ =\$1,251.03\end{array}$

Hence, the bond price of Bond T will be $1,251.03 when the interest declines to 5 percent.

Compute the percentage change in the price of Bond T when the interest rates decline to 5 percent:

The new price after the increase in interest rate is $1,251.03. The initial price of the bond was $1,000.

$\begin{array}{c}\text{Percentage change in price}=\frac{\text{New price}-\text{Initial price}}{\text{Initial price}}\times 100\\ =\frac{\$1,251.03-\$1,000}{\$1,000}\times 100\\ =\frac{\$251.03}{\$1,000}\times 100\\ =25.103\%\end{array}$

Hence, the percentage increase in the price of Bond T is 25.103 percent when the interest rates decline to 5 percent.

A summary of the bond prices and yield to maturity of Bond B and Bond T:

Table 1

Yield to maturity	Bond B	Bond T
5%	$1,055.08	$1,251.03
7%	$1,000.00	$1,000.00
9%	$948.42	$815.98

A graph indicating the relationship between bond prices and yield to maturity based on Table 1:

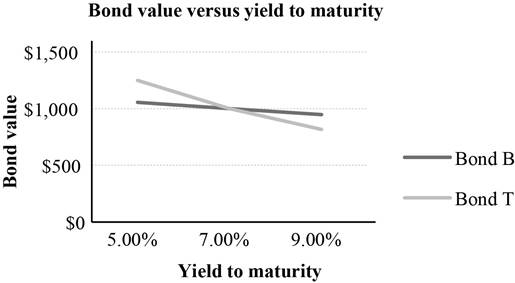
Interpretation of the graph:

The above graph indicates that the price fluctuation is higher in a bond with higher maturity. Bond T has a maturity period of 20 years. As its maturity period is longer, its price sensitivity to the interest rates is higher. Bond B has a maturity period of 3 years. As its maturity period is shorter, its price sensitivity to the interest rates is lower. Hence, a bond with longer maturity is subject to higher interest rate risk.