
Concept explainers
Find the slope
Answer to Problem 16P
The slope at point B of the given beam using the direct moment-area method is
The deflection at point B of the given beam using the direct moment-area method is
The slope at point C of the given beam using the direct moment-area method is
The deflection at point C of the given beam using the direct moment-area method is
Explanation of Solution
Given information:
The Young’s modulus (E) is 29,000 ksi.
The moment of inertia (I) is
Calculation:
Consider flexural rigidity EI of the beam is constant.
Show the free body diagram of the given beam as in Figure (1).

Refer Figure 1,
Consider upward is positive and downward is negative.
Consider clockwise is negative and counterclowise is positive.
Since support C is a free end there is no reaction.
Determine the bending moment at A;
Determine the bending moment at B;
Determine the moment at D;
Determine the bending moment at C;
Show the

Elastic curve:
The sign of
Show the elastic curve diagram as in Figure (3).
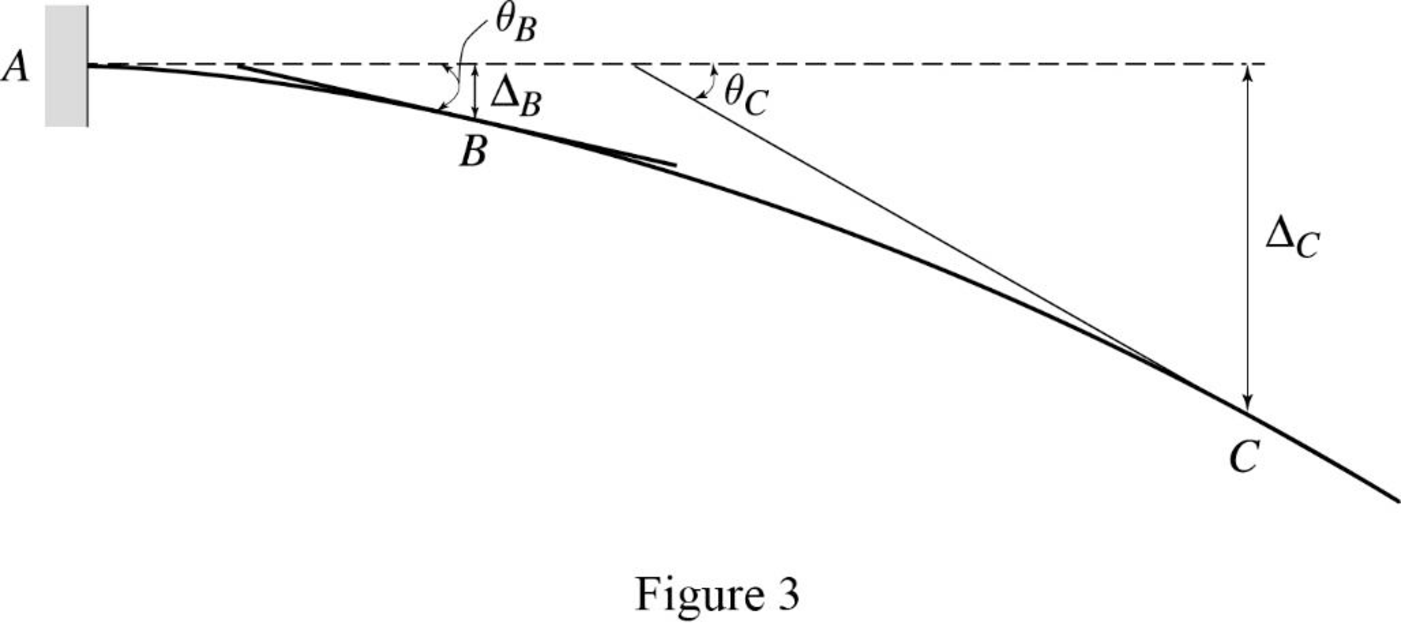
The slope at point B can be calculated by evaluating the change in slope between A and B.
Express the change in slope using the first moment-area theorem as follows:
Here, b is the width of the respective triangle and rectangle and h is the height of the respective triangle and rectangle.
Substitute 10 ft for b,
Determine the slope at B using the relation;
Substitute
Hence, the slope at point B is
The deflection of B with respect to the undeforemd axis of the beam is equal to the tangential deviation of B from the tangent at A.
Express the deflection at B using the second moment-area theorem as follows:
Substitute 10 ft for b,
Determine the deflection at B using the relation;
Substitute
Hence, the deflection at B is
Express the change in slope using the first moment-area theorem as follows:
Here, b is the width and h is the height of the rectangle, triangle, and parabola.
Substitute
Determine the slope at C using the relation;
Substitute
Hence, the slope at point C is
The deflection of C with respect to the undeforemd axis of the beam is equal to the tangential deviation of C from the tangent at A.
Express the deflection at C using the second moment-area theorem as follows:
Determine the deflection at C using the relation;
Substitute
Hence, the deflection at C is
Want to see more full solutions like this?
Chapter 6 Solutions
Structural Analysis, SI Edition
- A5.2- A simply supported beam with the given cross-section, as shown in Figure 2, is subjected to factored uniform load of 50 kN/m. The designer would like to cut-off 2-30M bars where they are no longer required by the design. Determine the cut-off point for 2-30M bars according to CSA 23.3 requirements. Given: Concrete: Normal density with f'c = 30 MPa Reinforcement: Uncoated rebars with fy = 400 MPa Shear reinforcement is in excess of CSA 23.3 minimum requirement: 10M Clear cover to the stirrups: 40 mm Columns: 500 mm x 500 mm 9 m W= 50 kN/m Figure 2 h=600 mm b=500 mm Cross-section As = 5-30Marrow_forward1. Calculate the ultimate load carrying capacity of the pile tip driven into the soil profile shown below: G.W.T. 45' Qapp Soft Clay: Ysat 100 pcf Cu 500 psf, ou = 0° 平 12' Soil Plug Driven Steel Pipe Pile: Outside Diameter = 2' Inside Diameter = 1'11" Hollow (soil plugged) Note: Pile & soil profile are not drawn to scale Qp = ? Please perform the tip capacity calculation two ways: For the first approach, assume that the total vertical stress at the pile tip is balanced by the weight of the pile. For the second approach, assume that the total vertical stress at the pile tip is not balanced by the weight of the pile (which means you need to include the vertical total stress term). Please compare your answers from these two analyses, examine some of your intermediate-stage calculation results such as the total overburden stress at the pile tip relative to the weight of the pile, and discuss whether or not the commonly used assumption about the total vertical stress at the pile tip is a…arrow_forwardA6.2- Given a simply supported beam with the typical cross-section as shown in the figure below. Assume interior exposure for this beam. The beam properties are summarized below. a) Check if the beam section satisfies the CSA A23.3 cracking control requirements. In your calculations, find f, accurately based on the loading, and compare the results with f = 0.6 fy. b) Find the deflection due to DL+LL at mid-span after 6 years. Given: Concrete: Normal density with f'c = 25 MPa Reinforcement: Uncoated rebars with fy = 400 MPa Shear reinforcement: 10M Maximum aggregate size: 20 mm Clear cover to the stirrup: 30 mm Clear spacing between the bars = 35 mm 35 mm 30 mm m WDL= 20 kN/m WLL= 15 kN/m 抖抖 b=400 mm As = 8-25M Cross-section h=500 mmarrow_forward
- A5.1- An unbraced column shown in Figure 1, column A-B with square cross-section is given. The column is subjected to Dead load (unfactored): PDL = 3000 kN, MDL-top = 85 kN.m, MDL-bo = -DL-bottom = 100 kN.m. = Assume the cross-section of column is constant from top to bottom, and all the beams have width = 300 mm and height 350 mm. Using f'c = 25 MPa, fy = 400 MPa, design the column and determine the ties spacing and arrangement. Use 25M or 30M bars for longitudinal reinforcement, and 10M bars for ties. Assume clear cover to be 40mm. The design p has to be between 0.01 and 0.02. Column maximum dimension can be 500mm. т 4.0m 7.0m 5.5m + 6.5m Figure 1 Barrow_forward7.43 Neglecting head losses, determine what horsepower the pump must deliver to produce the flow as shown. Here, the elevations at points A, B, C, and D are 124 ft, 161 ft, 110 ft, and 90 ft, respectively. The nozzle area is 0.10 ft². B Nozzle Water C D Problem 7.43arrow_forwardNOTE: Use areal methods only for V,M,N diagrams(Do NOT use the equations) (also draw the N diagram(s) for the entire structure)arrow_forward
- NOTE: Use areal methods only for V,M,N diagrams(Do NOT use the equations) (also draw the N diagram(s) for the entire structure)arrow_forwardNOTE: Use areal methods only for V,M,N diagrams(Do NOT use the equations) (also draw the N diagram(s) for the entire structure)arrow_forwardNOTE: Use areal methods only for V,M,N diagrams(Do NOT use the equations) (also draw the N diagram(s) for the entire structure)arrow_forward
- NOTE: Use areal methods only for V,M,N diagrams(Do NOT use the equations) (also draw the N diagram(s) for the entire structure)arrow_forwardNOTE: Use areal methods only for V,M,N diagrams(Do NOT use the equations) (also draw the N diagram(s) for the entire structure)arrow_forwardProblem 2: Use the table below to compute the coordinates of the centroid of area shown below. y – 3 in.—|— 4 in. - -3 3 in. 3 in. x Area X X * Area y Y * Area Component (in²) (in) (in³) (in) (in³) Square 1 Rectangle 2 Triangle 3 Rectangle 4 Σarrow_forward
