
In the following problem, we ask the reader to some of the details left out of the above discussion, to analyse the closed-loop system for the stability properties, and to conduct a numerical simulation of the nonlinear system.
Work out the details leading toEq. (1).
The expression for
Answer to Problem 1P
Solution:
The expression for the angle between the fly ball connecting arm and the vertical shaft is:
Explanation of Solution
Given information:
The model for the fly ball governor follows from taking into account all of the forces acting on the fly ball and applying Newton’s law,
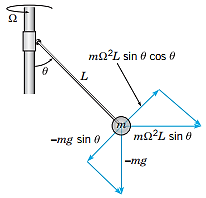
Explanation:
Let
By using the Newton’s second law of motion,
There are two forces acting on the point mass, one is gravity, which is in downward direction, so it is
The magnitude of the sum is easily found from the figure as
Also, for upward direction, the gravitational force is
Thus, the total magnitude of the sum is
But Newton’s second law of motion tells that the net force is the mass times the acceleration.
Let
Thus,
Therefore, the expression for the angle between the fly ball connecting arm and the vertical shaft is
Want to see more full solutions like this?
Chapter 5 Solutions
Differential Equations: An Introduction to Modern Methods and Applications
Additional Math Textbook Solutions
Elementary and Intermediate Algebra: Concepts and Applications (7th Edition)
Algebra and Trigonometry (6th Edition)
Introductory Statistics
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Precalculus: Mathematics for Calculus (Standalone Book)
College Algebra with Modeling & Visualization (5th Edition)
- 1. Explicitly compute by hand (with work shown) the following Frobenius inner products 00 4.56 3.12 (a) ((º º º). (156 (b) 10.9 -1 0 2)), Fro 5')) Froarrow_forward3. Let 4 0 0 00 0 0 1.2 0 00 0 0 0 -10.1 0 0 0 D = 0 0 0 00 0 0 0 0 05 0 0 0 0 0 0 2.8 Either explicitly compute D-¹ or explain why it doesn't exist.arrow_forward4. [9 points] Assume that B, C, E are all 3 x 3 matrices such that BC == -64 -1 0 3 4 4 4 -2 2 CB=-1-2 4 BE -2 1 3 EC = 1 3 2 -7, 1 6 -6 2-5 -7 -2 Explicitly compute the following by hand. (I.e., write out the entries of the 3 × 3 matrix.) (a) [3 points] B(E+C) (b) [3 points] (E+B)C (c) [3 points] ETBTarrow_forward
- 6. Consider the matrices G = 0 (3) -3\ -3 2 and H = -1 2 0 5 0 5 5 noting that H(:, 3) = 2H(:,1) + H(:, 2). Is G invertible? Explain your answer. Is H invertible? Explain your answer. Use co-factor expansion to find the determinant of H. (Hint: expand the 2nd or 3rd row)arrow_forwardB3 Consider X ~ Bern(p) (a) Find Mx(t), the moment generating function of X. iid (b) If X1,..., Xn Bern(p), find the MGF, say My (t) of n Y = ΣΧ (c) Using the fact that i=1 n lim (1 (1+2)"= N→X = e² find limn→∞ My (t) in the case that p satisfies limn→∞ np = λ, say. (d) State the distribution of Y in the case that n is not large, and the distribution of Y in the limiting case described in the question.arrow_forwardB1 The density of the x2 distribution is given in the notes as 1 F(§)2/2 (x)=()2/21 x/2-1/2, if x > 0, and e where I(t)=√xt-¹e dx is the gamma function. otherwise, Find the point at which o(a) has its maximum, i.e. find arg max, o, (x)arrow_forward
- For the matrix A = = ( 6 }) . explicitly compute by hand (with work shown) the following. I2A, where I2 is the 2 × 2 identity matrix. A-1 solving the following linear systems by using A-¹: c+y= 1 y = 1 (d) (e) (f) A² find the diagonal entries of Aarrow_forwardIf 3x−y=12, what is the value of 8x / 2y A) 212B) 44C) 82D) The value cannot be determined from the information given.arrow_forwardC=59(F−32) The equation above shows how temperature F, measured in degrees Fahrenheit, relates to a temperature C, measured in degrees Celsius. Based on the equation, which of the following must be true? A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 59 degree Celsius. A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit. A temperature increase of 59 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius. A) I onlyB) II onlyC) III onlyD) I and II onlyarrow_forward
- please answer the questions below ands provide the required codes in PYTHON. alsp provide explanation of how the codes were executed. Also make sure you provide codes that will be able to run even with different parameters as long as the output will be the same with any parameters given. these questions are not graded. provide accurate codes pleasearrow_forward(1) Let F be a field, show that the vector space F,NEZ* be a finite dimension. (2) Let P2(x) be the vector space of polynomial of degree equal or less than two and M={a+bx+cx²/a,b,cЄ R,a+b=c),show that whether Mis hyperspace or not. (3) Let A and B be a subset of a vector space such that ACB, show that whether: (a) if A is convex then B is convex or not. (b) if B is convex then A is convex or not. (4) Let R be a field of real numbers and X=R, X is a vector space over R show that by definition the norms/II.II, and II.112 on X are equivalent where Ilxll₁ = max(lx,l, i=1,2,...,n) and llxll₂=(x²). oper (5) Let Ⓡ be a field of real numbers, Ⓡis a normed space under usual operations and norm, let E=(2,5,8), find int(E), b(E) and D(E). (6) Write the definition of bounded linear function between two normed spaces and write with prove the relation between continuous and bounded linear function between two normed spaces.arrow_forwardind → 6 Q₁/(a) Let R be a field of real numbers and X-P(x)=(a+bx+cx²+dx/ a,b,c,dER},X is a vector space over R, show that is finite dimension. (b) Let be a bijective linear function from a finite dimension vector ✓ into a space Yand Sbe a basis for X, show that whether f(S) basis for or not. (c) Let be a vector space over a field F and A,B)affine subsets of X,show that whether aAn BB, aAU BB be affine subsets of X or not, a,ẞ EF. (12 Jal (answer only two) (6) Let M be a non-empty subset of a vector space X and tEX, show that M is a hyperspace of X iff t+M is a hyperplane of X and tЄt+M. (b) State Jahn-Banach theorem and write with prove an application of Hahn-arrow_forward
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning



