Chapter 56, Problem 18A

Solve the following exercises based on Principles 18 through 21, although an exercise may require the application oftwo or more of any of the principles. Where necessary, round linear answers in inches to 3 decimal places and millimeters to 2 decimal places. Round angular answers in decimal degrees to 2 decimal places and degrees and minutes to the nearest minute.

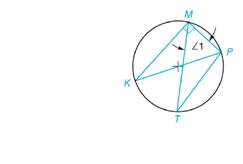
a. If ∠1 = 25°, find $\stackrel{⌢}{MPT}$= 95°, find
(1) $\stackrel{⌢}{KTP}$
(2) PT
(3) $\stackrel{⌢}{MP}$
b. If ∠1 = 17°30', find $\stackrel{⌢}{MPT}$= 103°, find
(1) $\stackrel{⌢}{KTP}$
(2) PT
(3) $\stackrel{⌢}{MP}$