Chapter 5.5, Problem 42PPSE

Solution

The greatest height that can be used for pyramid.

The maximum height of the pyramid is 5.2.

Given information: It is given that the height of the pyramid is 0.5cm less than twice the side length of the base of the pyramid.

It is given that we have $18c{m}^3$ of clay.

Explanation:

Let the length of side of the base of the pyramid be $x \text{cm}$ .

It is given that the height of the pyramid is $0.5 \text{cm}$ less than twice the side length of the base of the pyramid.

Therefore, Height $=2x-0.5$ .

It is given that there is $18 {\text{cm}}^3$ of clay.

For the height to be maximum, use all the available clay to make the pyramid.

The volume of the pyramid made by using $18 {\text{cm}}^3$ of clay will also be $18 {\text{cm}}^3$ .

  $\text{The volume of the pyramid=}\frac{\text{1}}{\text{3}}\text{×Area}\text{of}\text{the}\text{Base×Height}$

The base is square with side length $x$

Therefore, the area of base of the pyramid is $x^2$

Substitute Area of Base $=x^2$ and Height $=2x-0.5$

  $\begin{array}{c}\text{Volume}\text{of}\text{the}\text{pyramid}=\frac{1}{3}\left(x^2\right)\left(2x-\frac{1}{2}\right)\\ =\frac{2x^3}{3}-\frac{x^2}{6}\end{array}$

Volume of the pyramid is ${\text{18 cm}}^{\text{3}}$ . Therefore, we can write the equation

  $18=\frac{2x^3}{3}-\frac{x^2}{6}$

Multiply both sides by 6, to get

  $\begin{array}{c}108=4x^3-x^2\\ 4x^3-x^2-108=0\end{array}$

The graph for $y=4x^3-x^2-108$ is shown below:

  

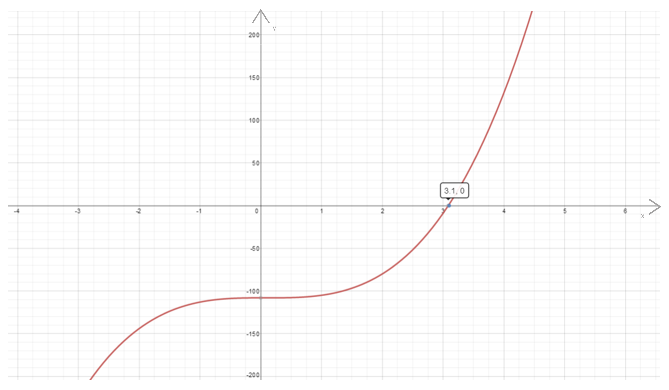
In the graph below note that the scales on $x$ and $y$ are different.

  $x=3.1$ is the only $x$ -intercept, therefore the equation $4x^3-x^2-108=0$ has only one root

Height of the pyramid is $2x-0.5$ .

Therefore, the maximum height of the pyramid is $2(3.1)-1=5.2$ .