PRECALCULUS:GRAPHICAL,...-NASTA ED.
10th Edition
ISBN: 9780134672090
Author: Demana
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Expert Solution & Answer
Chapter 5.4, Problem 63E
Solution
a)
To plot: The scatterplot of the given data of day of the year and time as the number of minutes past 18:30.
The scatterplot of the given data is shown below.
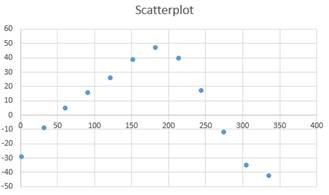
Given:The data of the year and time as the number of minutes past 18:30 is shown below
| Day | 18:30+ |
| 1 | -29 |
| 32 | -9 |
| 60 | 5 |
| 91 | 16 |
| 121 | 26 |
| 152 | 39 |
| 182 | 47 |
| 213 | 40 |
| 244 | 17 |
| 274 | -12 |
| 305 | -35 |
| 335 | -42 |
Plot:The data of the day of the year in L1 and the number of minutes past 18:30 in L2 and using this data a scatterplot is plotted as shown below
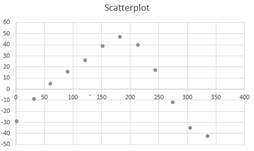
b)
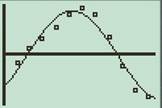
To plot: Superimpose the graph on the scatterplot and verify if it is a good fit.
The superimposing of the graph on scatterplot is shown below
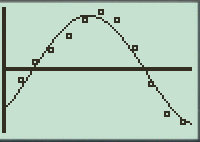
The model looks like a good fit.
Plot:
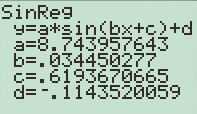
Press “STAT” in the calculator and then go to “CALC” menu and choose SinReg function and click enter. Select the data entered in L1 and L2 to plot the curve and click ok to get the following output and graph
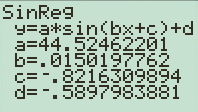
Interpretation:With reference to Sin regression output the regression equation is
c)
To calculate: The predicted y value and also the residual values for the given data.
The predicted values and residuals for the given data are shown below
| L1 (Day) | L2 (18:30+) | L3 | L4 |
| 1 | -29 | -32.68 | 3.68 |
| 32 | -9 | -15.44 | 6.44 |
| 60 | 5 | 2.97 | 2.03 |
| 91 | 16 | 22.49 | -6.49 |
| 121 | 26 | 36.76 | -10.76 |
| 152 | 39 | 43.66 | -4.66 |
| 182 | 47 | 41.40 | 5.60 |
| 213 | 40 | 30.30 | 9.70 |
| 244 | 17 | 12.64 | 4.36 |
| 274 | -12 | -7.17 | -4.83 |
| 305 | -35 | -26.22 | -8.78 |
| 335 | -42 | -39.50 | -2.50 |
Plot:
With reference to the data given in L1 and L2, column L3 shows the predicted values and column L4 shows residuals.
The predicted value in L3 is calculated by plugging in the values of x, and y in the regression equation as shown below
Similarly, for all values column L3 is created in the calculator and in column L4 the residuals are calculated using
| L1 (Day) | L2 (18:30+) | L3 | L4 |
| 1 | -29 | -32.68 | 3.68 |
| 32 | -9 | -15.44 | 6.44 |
| 60 | 5 | 2.97 | 2.03 |
| 91 | 16 | 22.49 | -6.49 |
| 121 | 26 | 36.76 | -10.76 |
| 152 | 39 | 43.66 | -4.66 |
| 182 | 47 | 41.40 | 5.60 |
| 213 | 40 | 30.30 | 9.70 |
| 244 | 17 | 12.64 | 4.36 |
| 274 | -12 | -7.17 | -4.83 |
| 305 | -35 | -26.22 | -8.78 |
| 335 | -42 | -39.50 | -2.50 |
d)
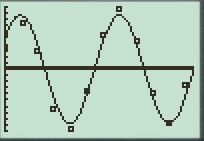
To plot: The scatterplot of the given data of day of the year in L1 and the residuals in L3.
The scatterplot of the data in L1 and the residuals is shown below
The sine regression equation is
Plot:The data of the day of the year in L1 and the residuals in L3 are used to generate the regression output by clicking on STAT and then to CALC menu. In the options mentioned SinReg option is selected and the appropriate data is entered and a scatterplot is plotted as shown below
e)
To Interpret: The two scatterplots obtained for the data in L1, L2 and L1, L3.
The two scatterplots of the data in L1, L2 and L1, L3 are shown below
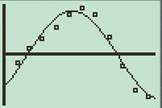
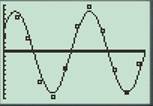
Both regressions indicate that the behaviour of the sunset as a function of time is sinusoidal.
Interpretation:
With reference to previous parts the scatter plots of the data L1, L2, and L1, L3 both have a sinusoidal graph. Thus there exists a periodic behavior of sunset with respect to time.
Chapter 5 Solutions
PRECALCULUS:GRAPHICAL,...-NASTA ED.
Ch. 5.1 - Prob. 1QRCh. 5.1 - Prob. 2QRCh. 5.1 - Prob. 3QRCh. 5.1 - Prob. 4QRCh. 5.1 - Prob. 5QRCh. 5.1 - Prob. 6QRCh. 5.1 - Prob. 7QRCh. 5.1 - Prob. 8QRCh. 5.1 - Prob. 9QRCh. 5.1 - Prob. 10QR
Ch. 5.1 - Prob. 11QRCh. 5.1 - Prob. 12QRCh. 5.1 - Prob. 1ECh. 5.1 - Prob. 2ECh. 5.1 - Prob. 3ECh. 5.1 - Prob. 4ECh. 5.1 - Prob. 5ECh. 5.1 - Prob. 6ECh. 5.1 - Prob. 7ECh. 5.1 - Prob. 8ECh. 5.1 - Prob. 9ECh. 5.1 - Prob. 10ECh. 5.1 - Prob. 11ECh. 5.1 - Prob. 12ECh. 5.1 - Prob. 13ECh. 5.1 - Prob. 14ECh. 5.1 - Prob. 15ECh. 5.1 - Prob. 16ECh. 5.1 - Prob. 17ECh. 5.1 - Prob. 18ECh. 5.1 - Prob. 19ECh. 5.1 - Prob. 20ECh. 5.1 - Prob. 21ECh. 5.1 - Prob. 22ECh. 5.1 - Prob. 23ECh. 5.1 - Prob. 24ECh. 5.1 - Prob. 25ECh. 5.1 - Prob. 26ECh. 5.1 - Prob. 27ECh. 5.1 - Prob. 28ECh. 5.1 - Prob. 29ECh. 5.1 - Prob. 30ECh. 5.1 - Prob. 31ECh. 5.1 - Prob. 32ECh. 5.1 - Prob. 33ECh. 5.1 - Prob. 34ECh. 5.1 - Prob. 35ECh. 5.1 - Prob. 36ECh. 5.1 - Prob. 37ECh. 5.1 - Prob. 38ECh. 5.1 - Prob. 39ECh. 5.1 - Prob. 40ECh. 5.1 - Prob. 41ECh. 5.1 - Prob. 42ECh. 5.1 - Prob. 43ECh. 5.1 - Prob. 44ECh. 5.1 - Prob. 45ECh. 5.1 - Prob. 46ECh. 5.1 - Prob. 47ECh. 5.1 - Prob. 48ECh. 5.1 - Prob. 49ECh. 5.1 - Prob. 50ECh. 5.1 - Prob. 51ECh. 5.1 - Prob. 52ECh. 5.1 - Prob. 53ECh. 5.1 - Prob. 54ECh. 5.1 - Prob. 55ECh. 5.1 - Prob. 56ECh. 5.1 - Prob. 57ECh. 5.1 - Prob. 58ECh. 5.1 - Prob. 59ECh. 5.1 - Prob. 60ECh. 5.1 - Prob. 61ECh. 5.1 - Prob. 62ECh. 5.1 - Prob. 63ECh. 5.1 - Prob. 64ECh. 5.1 - Prob. 65ECh. 5.1 - Prob. 66ECh. 5.1 - Prob. 67ECh. 5.1 - Prob. 68ECh. 5.1 - Prob. 69ECh. 5.1 - Prob. 70ECh. 5.1 - Prob. 71ECh. 5.1 - Prob. 72ECh. 5.1 - Prob. 73ECh. 5.1 - Prob. 74ECh. 5.1 - Prob. 75ECh. 5.1 - Prob. 76ECh. 5.1 - Prob. 77ECh. 5.1 - Prob. 78ECh. 5.1 - Prob. 79ECh. 5.1 - Prob. 80ECh. 5.1 - Prob. 81ECh. 5.1 - Prob. 82ECh. 5.1 - Prob. 83ECh. 5.1 - Prob. 84ECh. 5.1 - Prob. 85ECh. 5.1 - Prob. 87ECh. 5.1 - Prob. 88ECh. 5.1 - Prob. 89ECh. 5.1 - Prob. 90ECh. 5.1 - Prob. 91ECh. 5.1 - Prob. 92ECh. 5.2 - Prob. 1QRCh. 5.2 - Prob. 2QRCh. 5.2 - Prob. 3QRCh. 5.2 - Prob. 4QRCh. 5.2 - Prob. 5QRCh. 5.2 - Prob. 6QRCh. 5.2 - Prob. 7QRCh. 5.2 - Prob. 8QRCh. 5.2 - Prob. 9QRCh. 5.2 - Prob. 10QRCh. 5.2 - Prob. 11QRCh. 5.2 - Prob. 12QRCh. 5.2 - Prob. 1ECh. 5.2 - Prob. 2ECh. 5.2 - Prob. 3ECh. 5.2 - Prob. 4ECh. 5.2 - Prob. 5ECh. 5.2 - Prob. 6ECh. 5.2 - Prob. 7ECh. 5.2 - Prob. 8ECh. 5.2 - Prob. 9ECh. 5.2 - Prob. 10ECh. 5.2 - Prob. 11ECh. 5.2 - Prob. 12ECh. 5.2 - Prob. 13ECh. 5.2 - Prob. 14ECh. 5.2 - Prob. 15ECh. 5.2 - Prob. 16ECh. 5.2 - Prob. 17ECh. 5.2 - Prob. 18ECh. 5.2 - Prob. 19ECh. 5.2 - Prob. 20ECh. 5.2 - Prob. 21ECh. 5.2 - Prob. 22ECh. 5.2 - Prob. 23ECh. 5.2 - Prob. 24ECh. 5.2 - Prob. 25ECh. 5.2 - Prob. 26ECh. 5.2 - Prob. 27ECh. 5.2 - Prob. 28ECh. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Prob. 31ECh. 5.2 - Prob. 32ECh. 5.2 - Prob. 33ECh. 5.2 - Prob. 34ECh. 5.2 - Prob. 35ECh. 5.2 - Prob. 36ECh. 5.2 - Prob. 37ECh. 5.2 - Prob. 38ECh. 5.2 - Prob. 39ECh. 5.2 - Prob. 40ECh. 5.2 - Prob. 41ECh. 5.2 - Prob. 42ECh. 5.2 - Prob. 43ECh. 5.2 - Prob. 44ECh. 5.2 - Prob. 45ECh. 5.2 - Prob. 46ECh. 5.2 - Prob. 47ECh. 5.2 - Prob. 48ECh. 5.2 - Prob. 49ECh. 5.2 - Prob. 50ECh. 5.2 - Prob. 51ECh. 5.2 - Prob. 52ECh. 5.2 - Prob. 53ECh. 5.2 - Prob. 54ECh. 5.2 - Prob. 55ECh. 5.2 - Prob. 56ECh. 5.2 - Prob. 57ECh. 5.2 - Prob. 58ECh. 5.2 - Prob. 59ECh. 5.2 - Prob. 60ECh. 5.2 - Prob. 61ECh. 5.2 - Prob. 62ECh. 5.2 - Prob. 63ECh. 5.2 - Prob. 64ECh. 5.2 - Prob. 65ECh. 5.2 - Prob. 66ECh. 5.2 - Prob. 67ECh. 5.2 - Prob. 68ECh. 5.2 - Prob. 69ECh. 5.2 - Prob. 70ECh. 5.2 - Prob. 71ECh. 5.2 - Prob. 73ECh. 5.2 - Prob. 74ECh. 5.2 - Prob. 75ECh. 5.2 - Prob. 76ECh. 5.2 - Prob. 77ECh. 5.2 - Prob. 78ECh. 5.2 - Prob. 79ECh. 5.2 - Prob. 80ECh. 5.2 - Prob. 81ECh. 5.3 - Prob. 1QRCh. 5.3 - Prob. 2QRCh. 5.3 - Prob. 3QRCh. 5.3 - Prob. 4QRCh. 5.3 - Prob. 5QRCh. 5.3 - Prob. 6QRCh. 5.3 - Prob. 7QRCh. 5.3 - Prob. 8QRCh. 5.3 - Prob. 9QRCh. 5.3 - Prob. 10QRCh. 5.3 - Prob. 1ECh. 5.3 - Prob. 2ECh. 5.3 - Prob. 3ECh. 5.3 - Prob. 4ECh. 5.3 - Prob. 5ECh. 5.3 - Prob. 6ECh. 5.3 - Prob. 7ECh. 5.3 - Prob. 8ECh. 5.3 - Prob. 9ECh. 5.3 - Prob. 10ECh. 5.3 - Prob. 11ECh. 5.3 - Prob. 12ECh. 5.3 - Prob. 13ECh. 5.3 - Prob. 14ECh. 5.3 - Prob. 15ECh. 5.3 - Prob. 16ECh. 5.3 - Prob. 17ECh. 5.3 - Prob. 18ECh. 5.3 - Prob. 19ECh. 5.3 - Prob. 20ECh. 5.3 - Prob. 21ECh. 5.3 - Prob. 22ECh. 5.3 - Prob. 23ECh. 5.3 - Prob. 24ECh. 5.3 - Prob. 25ECh. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - Prob. 28ECh. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - Prob. 31ECh. 5.3 - Prob. 32ECh. 5.3 - Prob. 33ECh. 5.3 - Prob. 34ECh. 5.3 - Prob. 35ECh. 5.3 - Prob. 36ECh. 5.3 - Prob. 37ECh. 5.3 - Prob. 38ECh. 5.3 - Prob. 39ECh. 5.3 - Prob. 40ECh. 5.3 - Prob. 41ECh. 5.3 - Prob. 42ECh. 5.3 - Prob. 43ECh. 5.3 - Prob. 44ECh. 5.3 - Prob. 45ECh. 5.3 - Prob. 46ECh. 5.3 - Prob. 47ECh. 5.3 - Prob. 48ECh. 5.3 - Prob. 49ECh. 5.3 - Prob. 50ECh. 5.3 - Prob. 51ECh. 5.3 - Prob. 52ECh. 5.3 - Prob. 53ECh. 5.3 - Prob. 54ECh. 5.3 - Prob. 55ECh. 5.3 - Prob. 56ECh. 5.3 - Prob. 57ECh. 5.3 - Prob. 58ECh. 5.3 - Prob. 59ECh. 5.3 - Prob. 60ECh. 5.3 - Prob. 61ECh. 5.3 - Prob. 62ECh. 5.3 - Prob. 63ECh. 5.3 - Prob. 64ECh. 5.3 - Prob. 65ECh. 5.3 - Prob. 66ECh. 5.3 - Prob. 67ECh. 5.3 - Prob. 69ECh. 5.3 - Prob. 70ECh. 5.3 - Prob. 71ECh. 5.3 - Prob. 72ECh. 5.3 - Prob. 73ECh. 5.3 - Prob. 74ECh. 5.3 - Prob. 75ECh. 5.4 - Prob. 1QRCh. 5.4 - Prob. 2QRCh. 5.4 - Prob. 3QRCh. 5.4 - Prob. 4QRCh. 5.4 - Prob. 5QRCh. 5.4 - Prob. 6QRCh. 5.4 - Prob. 7QRCh. 5.4 - Prob. 8QRCh. 5.4 - Prob. 9QRCh. 5.4 - Prob. 10QRCh. 5.4 - Prob. 1ECh. 5.4 - Prob. 2ECh. 5.4 - Prob. 3ECh. 5.4 - Prob. 4ECh. 5.4 - Prob. 5ECh. 5.4 - Prob. 6ECh. 5.4 - Prob. 7ECh. 5.4 - Prob. 8ECh. 5.4 - Prob. 9ECh. 5.4 - Prob. 10ECh. 5.4 - Prob. 11ECh. 5.4 - Prob. 12ECh. 5.4 - Prob. 13ECh. 5.4 - Prob. 14ECh. 5.4 - Prob. 15ECh. 5.4 - Prob. 16ECh. 5.4 - Prob. 17ECh. 5.4 - Prob. 18ECh. 5.4 - Prob. 19ECh. 5.4 - Prob. 20ECh. 5.4 - Prob. 21ECh. 5.4 - Prob. 22ECh. 5.4 - Prob. 23ECh. 5.4 - Prob. 24ECh. 5.4 - Prob. 25ECh. 5.4 - Prob. 26ECh. 5.4 - Prob. 27ECh. 5.4 - Prob. 28ECh. 5.4 - Prob. 29ECh. 5.4 - Prob. 30ECh. 5.4 - Prob. 31ECh. 5.4 - Prob. 32ECh. 5.4 - Prob. 33ECh. 5.4 - Prob. 34ECh. 5.4 - Prob. 35ECh. 5.4 - Prob. 36ECh. 5.4 - Prob. 37ECh. 5.4 - Prob. 38ECh. 5.4 - Prob. 39ECh. 5.4 - Prob. 40ECh. 5.4 - Prob. 41ECh. 5.4 - Prob. 42ECh. 5.4 - Prob. 43ECh. 5.4 - Prob. 44ECh. 5.4 - Prob. 45ECh. 5.4 - Prob. 46ECh. 5.4 - Prob. 47ECh. 5.4 - Prob. 48ECh. 5.4 - Prob. 49ECh. 5.4 - Prob. 50ECh. 5.4 - Prob. 51ECh. 5.4 - Prob. 52ECh. 5.4 - Prob. 53ECh. 5.4 - Prob. 54ECh. 5.4 - Prob. 55ECh. 5.4 - Prob. 56ECh. 5.4 - Prob. 57ECh. 5.4 - Prob. 58ECh. 5.4 - Prob. 59ECh. 5.4 - Prob. 60ECh. 5.4 - Prob. 61ECh. 5.4 - Prob. 62ECh. 5.4 - Prob. 63ECh. 5.5 - Prob. 1QRCh. 5.5 - Prob. 2QRCh. 5.5 - Prob. 3QRCh. 5.5 - Prob. 4QRCh. 5.5 - Prob. 5QRCh. 5.5 - Prob. 6QRCh. 5.5 - Prob. 7QRCh. 5.5 - Prob. 8QRCh. 5.5 - Prob. 9QRCh. 5.5 - Prob. 10QRCh. 5.5 - Prob. 1ECh. 5.5 - Prob. 2ECh. 5.5 - Prob. 3ECh. 5.5 - Prob. 4ECh. 5.5 - Prob. 5ECh. 5.5 - Prob. 6ECh. 5.5 - Prob. 7ECh. 5.5 - Prob. 8ECh. 5.5 - Prob. 9ECh. 5.5 - Prob. 10ECh. 5.5 - Prob. 11ECh. 5.5 - Prob. 12ECh. 5.5 - Prob. 13ECh. 5.5 - Prob. 14ECh. 5.5 - Prob. 15ECh. 5.5 - Prob. 16ECh. 5.5 - Prob. 17ECh. 5.5 - Prob. 18ECh. 5.5 - Prob. 19ECh. 5.5 - Prob. 20ECh. 5.5 - Prob. 21ECh. 5.5 - Prob. 22ECh. 5.5 - Prob. 23ECh. 5.5 - Prob. 24ECh. 5.5 - Prob. 25ECh. 5.5 - Prob. 26ECh. 5.5 - Prob. 27ECh. 5.5 - Prob. 28ECh. 5.5 - Prob. 29ECh. 5.5 - Prob. 30ECh. 5.5 - Prob. 31ECh. 5.5 - Prob. 32ECh. 5.5 - Prob. 33ECh. 5.5 - Prob. 34ECh. 5.5 - Prob. 35ECh. 5.5 - Prob. 36ECh. 5.5 - Prob. 37ECh. 5.5 - Prob. 38ECh. 5.5 - Prob. 39ECh. 5.5 - Prob. 40ECh. 5.5 - Prob. 41ECh. 5.5 - Prob. 42ECh. 5.5 - Prob. 43ECh. 5.5 - Prob. 44ECh. 5.5 - Prob. 45ECh. 5.5 - Prob. 46ECh. 5.5 - Prob. 47ECh. 5.5 - Prob. 48ECh. 5.5 - Prob. 49ECh. 5.5 - Prob. 50ECh. 5.5 - Prob. 51ECh. 5.5 - Prob. 52ECh. 5.5 - Prob. 53ECh. 5.5 - Prob. 54ECh. 5.5 - Prob. 55ECh. 5.5 - Prob. 56ECh. 5.5 - Prob. 57ECh. 5.6 - Prob. 1QRCh. 5.6 - Prob. 2QRCh. 5.6 - Prob. 3QRCh. 5.6 - Prob. 4QRCh. 5.6 - Prob. 5QRCh. 5.6 - Prob. 6QRCh. 5.6 - Prob. 7QRCh. 5.6 - Prob. 8QRCh. 5.6 - Prob. 9QRCh. 5.6 - Prob. 10QRCh. 5.6 - Prob. 1ECh. 5.6 - Prob. 2ECh. 5.6 - Prob. 3ECh. 5.6 - Prob. 4ECh. 5.6 - Prob. 5ECh. 5.6 - Prob. 6ECh. 5.6 - Prob. 7ECh. 5.6 - Prob. 8ECh. 5.6 - Prob. 9ECh. 5.6 - Prob. 10ECh. 5.6 - Prob. 11ECh. 5.6 - Prob. 12ECh. 5.6 - Prob. 13ECh. 5.6 - Prob. 14ECh. 5.6 - Prob. 15ECh. 5.6 - Prob. 16ECh. 5.6 - Prob. 17ECh. 5.6 - Prob. 18ECh. 5.6 - Prob. 19ECh. 5.6 - Prob. 20ECh. 5.6 - Prob. 21ECh. 5.6 - Prob. 22ECh. 5.6 - Prob. 23ECh. 5.6 - Prob. 24ECh. 5.6 - Prob. 25ECh. 5.6 - Prob. 26ECh. 5.6 - Prob. 27ECh. 5.6 - Prob. 28ECh. 5.6 - Prob. 29ECh. 5.6 - Prob. 30ECh. 5.6 - Prob. 31ECh. 5.6 - Prob. 32ECh. 5.6 - Prob. 33ECh. 5.6 - Prob. 34ECh. 5.6 - Prob. 35ECh. 5.6 - Prob. 36ECh. 5.6 - Prob. 37ECh. 5.6 - Prob. 38ECh. 5.6 - Prob. 39ECh. 5.6 - Prob. 40ECh. 5.6 - Prob. 41ECh. 5.6 - Prob. 42ECh. 5.6 - Prob. 43ECh. 5.6 - Prob. 44ECh. 5.6 - Prob. 45ECh. 5.6 - Prob. 46ECh. 5.6 - Prob. 47ECh. 5.6 - Prob. 48ECh. 5.6 - Prob. 49ECh. 5.6 - Prob. 50ECh. 5.6 - Prob. 51ECh. 5.6 - Prob. 52ECh. 5.6 - Prob. 53ECh. 5.6 - Prob. 54ECh. 5.6 - Prob. 55ECh. 5 - Prob. 1RECh. 5 - Prob. 2RECh. 5 - Prob. 3RECh. 5 - Prob. 4RECh. 5 - Prob. 5RECh. 5 - Prob. 6RECh. 5 - Prob. 7RECh. 5 - Prob. 8RECh. 5 - Prob. 9RECh. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Prob. 12RECh. 5 - Prob. 13RECh. 5 - Prob. 14RECh. 5 - Prob. 15RECh. 5 - Prob. 16RECh. 5 - Prob. 17RECh. 5 - Prob. 18RECh. 5 - Prob. 19RECh. 5 - Prob. 20RECh. 5 - Prob. 21RECh. 5 - Prob. 22RECh. 5 - Prob. 23RECh. 5 - Prob. 24RECh. 5 - Prob. 25RECh. 5 - Prob. 26RECh. 5 - Prob. 27RECh. 5 - Prob. 28RECh. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - Prob. 33RECh. 5 - Prob. 34RECh. 5 - Prob. 35RECh. 5 - Prob. 36RECh. 5 - Prob. 37RECh. 5 - Prob. 38RECh. 5 - Prob. 39RECh. 5 - Prob. 40RECh. 5 - Prob. 41RECh. 5 - Prob. 42RECh. 5 - Prob. 43RECh. 5 - Prob. 44RECh. 5 - Prob. 45RECh. 5 - Prob. 46RECh. 5 - Prob. 47RECh. 5 - Prob. 48RECh. 5 - Prob. 49RECh. 5 - Prob. 50RECh. 5 - Prob. 51RECh. 5 - Prob. 52RECh. 5 - Prob. 53RECh. 5 - Prob. 54RECh. 5 - Prob. 55RECh. 5 - Prob. 56RECh. 5 - Prob. 57RECh. 5 - Prob. 58RECh. 5 - Prob. 59RECh. 5 - Prob. 60RECh. 5 - Prob. 61RECh. 5 - Prob. 62RECh. 5 - Prob. 63RECh. 5 - Prob. 64RECh. 5 - Prob. 65RECh. 5 - Prob. 66RECh. 5 - Prob. 67RECh. 5 - Prob. 68RECh. 5 - Prob. 69RECh. 5 - Prob. 70RECh. 5 - Prob. 71RECh. 5 - Prob. 72RECh. 5 - Prob. 73RECh. 5 - Prob. 74RECh. 5 - Prob. 75RECh. 5 - Prob. 76RECh. 5 - Prob. 77RE
Knowledge Booster
Similar questions
- Let f be a function whose graph consists of 5 line segments and a semicircle as shown in the figure below. Let g(x) = √ƒƒ(t) dt . 0 3 2 -2 2 4 5 6 7 8 9 10 11 12 13 14 15 1. g(0) = 2. g(2) = 3. g(4) = 4. g(6) = 5. g'(3) = 6. g'(13)=arrow_forwardThe expression 3 | (3+1/+1) of the following integrals? A Ов E + + + + 18 3+1+1 3++1 3++1 (A) √2×14 dx x+1 (C) 1½-½√ √ ² ( 14 ) d x (B) √31dx (D) So 3+x -dx is a Riemann sum approximation of which 5 (E) 1½√√3dx 2x+1arrow_forward2. Suppose the population of Wakanda t years after 2000 is given by the equation f(t) = 45000(1.006). If this trend continues, in what year will the population reach 50,000 people? Show all your work, round your answer to two decimal places, and include units. (4 points)arrow_forward
- 3. Solve the equation, give the answer exactly (no calculator approximations), and show all your work. (4 points) log5 2x = 3arrow_forwardLet I = f(x) dx, where f is the function whose graph is shown. 4 2 y f X 1 2 3 4 (a) Use the graph to find L2, R2 and M2. R₂ M2 = = = (b) Are these underestimates or overestimates of I? O 42 is an underestimate. O 42 is an overestimate. ◇ R2 is an underestimate. OR2 is an overestimate. OM2 is an underestimate. ○ M2 is an overestimate. (c) Use the graph to find T2. T₂ =arrow_forwardVector u has a magnitude of 23 and vector v has a magnitude of 83. The angle between the two vectors is 126 degrees.a) Draw a fully-labelled vector diagram showing the two vectors and the resultant vector when they are added together.b) Find the magnitude of the resultant vector.c) Find the direction of the resultant vector relative to vector u. Solding by finding the x and y of the vectors and addingarrow_forward
- 3) If a is a positive number, what is the value of the following double integral? 2a Love Lv 2ay-y² .x2 + y2 dadyarrow_forward16. Solve each of the following equations for x. (a) 42x+1 = 64 (b) 27-3815 (c) 92. 27² = 3-1 (d) log x + log(x - 21) = 2 (e) 3 = 14 (f) 2x+1 = 51-2xarrow_forward11. Find the composition fog and gof for the following functions. 2 (a) f(x) = 2x+5, g(x) = x² 2 (b) f(x) = x²+x, g(x) = √√x 1 (c) f(x) = -1/2) 9 9(x) = х = - Xarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning