
Concept explainers
The centroid of the section.
Answer to Problem 5.134P
The centroid of the section
Explanation of Solution
Refer Figure 1 and Figure 2.
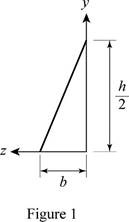
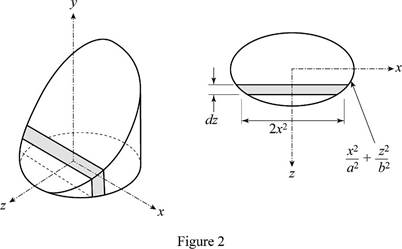
Consider an elemental section of the given section.
Write an expression to calculate the volume of the element.
Here,
From the symmetry, write an expression to calculate the distance of centroid of the section from x-axis.
Here,
From the symmetry, write an expression to calculate the distance of centroid of the section from x-axis.
Here,
Write an expression to calculate the distance of centroid of element from z-axis.
Here,
Write an expression to calculate width of the element.
Here,
Write an expression to calculate the height of the element.
Here,
Write an expression to calculate the volume of the section.
Write an expression to calculate the thickness of the section.
Differentiate the equation to calculate the thickness of the element.
Write an expression to find the distance of the centroid of the section from x axis.
Here,
Write an expression to find the distance of the centroid of the section from x axis.
Here,
Write an expression to find the distance of the centroid of the section from z axis.
Here,
Conclusion:
Substitute (V), (VI) and (IX) in equation (VII) to find
write an expression to calculate the distance of centroid of the element from x-axis.
Write an expression to calculate
Substitute equation (XIII) and (XIV) in equation (XI) to find
Write an expression to calculate
Substitute equation (XIII) and (XV) in equation (XII) to find
Thus, the centroid of the section
Want to see more full solutions like this?
Chapter 5 Solutions
VECTOR MECHANICS FOR ENGINEERS W/CON >B
- ##2# Superheated steam powers a steam turbine for the production of electrical energy. The steam expands in the turbine and at an intermediate expansion pressure (0.1 Mpa) a fraction is extracted for a regeneration process in a surface regenerator. The turbine has an isentropic efficiency of 90% Design the simplified power plant schematic Analyze it on the basis of the attached figure Determine the power generated and the thermal efficiency of the plant ### Dados in the attached imagesarrow_forward### To make a conclusion for a report of an experiment on rockets, in which the openrocket software was used for the construction and modeling of two rockets: one one-stage and one two-stage. First rocket (single-stage) reached a maximum vertical speed of 100 m/s and a maximum height of 500 m The second rocket (two-stage) reached a maximum vertical speed of 50 m/s and a maximum height of 250 m To make a simplified conclusion, taking into account the efficiency of the software in the study of rocketsarrow_forwardDetermine the coefficients of polynomial for the polynomial function of Cam profile based on the boundary conditions shown in the figure. S a 3 4 5 C₁ (+) Ꮎ В s = q + q { + c f * + q € * + q ( +c+c+c 6 Ꮎ +C5 +C β В В 0 cam angle 0 B 7 (arrow_forward
- ### Superheated steam powers a steam turbine for the production of electrical energy. The steam expands in the turbine and at an intermediate expansion pressure (0.1 Mpa) a fraction is extracted for a regeneration process in a surface regenerator. The turbine has an isentropic efficiency of 90% Design the simplified power plant schematic Analyze it on the basis of the attached figure Determine the power generated and the thermal efficiency of the plant ### Dados in the attached imagesarrow_forwardThe machine below forms metal plates through the application of force. Two toggles (ABC and DEF) transfer forces from the central hydraulic cylinder (H) to the plates that will be formed. The toggles then push bar G to the right, which then presses a plate (p) into the cavity, thus shaping it. In this case, the plate becomes a section of a sphere. If the hydraulic cylinder can produce a maximum force of F = 10 kN, then what is the maximum P value (i.e. Pmax) that can be applied to the plate when θ = 35°? Also, what are the compressive forces in the toggle rods in that situation? Finally, what happens to Pmax and the forces in the rods as θ decreases in magnitude?arrow_forwardDetermine the magnitude of the minimum force P needed to prevent the 20 kg uniform rod AB from sliding. The contact surface at A is smooth, whereas the coefficient of static friction between the rod and the floor is μs = 0.3.arrow_forward
- Determine the magnitudes of the reactions at the fixed support at A.arrow_forwardLet Hill frame H = {i-hat_r, i-hat_θ, i-hat_h} be the orbit frame of the LMO satellite. These base vectors are generally defined as:i-hat_r = r_LM / |r_LM|, i-hat_theta = i-hat_h X i-hat_r, i-hat_h = r_LM X r-dot_LMO /( | r_LM X r-dot_LMO | ) How would you: • Determine an analytic expressions for [HN]arrow_forwardDe Moivre’s Theoremarrow_forward
- hand-written solutions only, please.arrow_forwardDetermine the shear flow qqq for the given profile when the shear forces acting at the torsional center are Qy=30Q_y = 30Qy=30 kN and Qz=20Q_z = 20Qz=20 kN. Also, calculate qmaxq_{\max}qmax and τmax\tau_{\max}τmax. Given:Iy=10.5×106I_y = 10.5 \times 10^6Iy=10.5×106 mm4^44,Iz=20.8×106I_z = 20.8 \times 10^6Iz=20.8×106 mm4^44,Iyz=6×106I_{yz} = 6 \times 10^6Iyz=6×106 mm4^44. Additional parameters:αy=0.5714\alpha_y = 0.5714αy=0.5714,αz=0.2885\alpha_z = 0.2885αz=0.2885,γ=1.1974\gamma = 1.1974γ=1.1974. (Check hint: τmax\tau_{\max}τmax should be approximately 30 MPa.)arrow_forwardhand-written solutions only, please.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





