BIG IDEAS MATH Integrated Math 1: Student Edition 2016
16th Edition
ISBN: 9781680331127
Author: HOUGHTON MIFFLIN HARCOURT
Publisher: Houghton Mifflin Harcourt
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 5.4, Problem 2E
To determine
To explain:
The difference between the graph of a system of linear equations that has infinitely many solutions and no solution
Expert Solution & Answer
Answer to Problem 2E
A system of linear equations that has infinitely many solutions is single line graph which shows that it has the system of two linear equations are same.
A system of linear equations that has no solution is parallel line graph which shows that it has the linear equations do not intersect.
Explanation of Solution
A system of linear equations is formed by two equations. The solution of a system of equations is an ordered pair which satisfies these two equations successfully.
The number of solutions of system of linear equations has categorized as:
- No solution
- One solution
- Infinitely many solutions
Graph of system of linear equations that has infinitely many solutions:
A graph of two linear equations or system is said to be infinitely many solutions graph when the equations are same. When the system of linear equations has exactly same equation is known as dependent system.
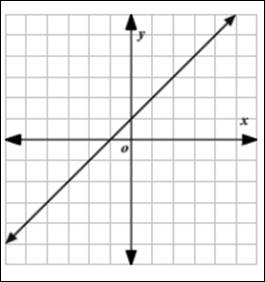
The system of linear equations that has infinitely many solutions is a single line graph.
Graph of system of linear equations that no solution:
When the graphs of linear equations do not intersect with each other, it is said to be that the system linear equations has no solution.
The system of linear equations with no solution is known as inconsistent system.
The graph of system of linear equations that no solution is parallel line graph which is shown by the following figure:
Chapter 5 Solutions
BIG IDEAS MATH Integrated Math 1: Student Edition 2016
Ch. 5.1 - Prob. 1ECh. 5.1 - Prob. 2ECh. 5.1 - Prob. 3ECh. 5.1 - Prob. 4ECh. 5.1 - Prob. 5ECh. 5.1 - Prob. 6ECh. 5.1 - Prob. 7ECh. 5.1 - Prob. 8ECh. 5.1 - Prob. 9ECh. 5.1 - Prob. 10E
Ch. 5.1 - Prob. 11ECh. 5.1 - Prob. 12ECh. 5.1 - Prob. 13ECh. 5.1 - Prob. 14ECh. 5.1 - Prob. 15ECh. 5.1 - Prob. 16ECh. 5.1 - Prob. 17ECh. 5.1 - Prob. 18ECh. 5.1 - Prob. 19ECh. 5.1 - Prob. 20ECh. 5.1 - Prob. 21ECh. 5.1 - Prob. 22ECh. 5.1 - Prob. 23ECh. 5.1 - Prob. 24ECh. 5.1 - Prob. 25ECh. 5.1 - Prob. 26ECh. 5.1 - Prob. 27ECh. 5.1 - Prob. 28ECh. 5.1 - Prob. 29ECh. 5.1 - Prob. 30ECh. 5.1 - Prob. 31ECh. 5.1 - Prob. 32ECh. 5.1 - Prob. 33ECh. 5.1 - Prob. 34ECh. 5.1 - Prob. 35ECh. 5.1 - Prob. 36ECh. 5.2 - Prob. 1ECh. 5.2 - Prob. 2ECh. 5.2 - Prob. 3ECh. 5.2 - Prob. 4ECh. 5.2 - Prob. 5ECh. 5.2 - Prob. 6ECh. 5.2 - Prob. 7ECh. 5.2 - Prob. 8ECh. 5.2 - Prob. 9ECh. 5.2 - Prob. 10ECh. 5.2 - Prob. 11ECh. 5.2 - Prob. 12ECh. 5.2 - Prob. 13ECh. 5.2 - Prob. 14ECh. 5.2 - Prob. 15ECh. 5.2 - Prob. 16ECh. 5.2 - Prob. 17ECh. 5.2 - Prob. 18ECh. 5.2 - Prob. 19ECh. 5.2 - Prob. 20ECh. 5.2 - Prob. 21ECh. 5.2 - Prob. 22ECh. 5.2 - Prob. 23ECh. 5.2 - Prob. 24ECh. 5.2 - Prob. 25ECh. 5.2 - Prob. 26ECh. 5.2 - Prob. 27ECh. 5.2 - Prob. 28ECh. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Prob. 31ECh. 5.2 - Prob. 32ECh. 5.2 - Prob. 33ECh. 5.2 - Prob. 34ECh. 5.2 - Prob. 35ECh. 5.2 - Prob. 36ECh. 5.2 - Prob. 37ECh. 5.2 - Prob. 38ECh. 5.2 - Prob. 39ECh. 5.2 - Prob. 40ECh. 5.2 - Prob. 41ECh. 5.3 - Prob. 1ECh. 5.3 - Prob. 2ECh. 5.3 - Prob. 3ECh. 5.3 - Prob. 4ECh. 5.3 - Prob. 5ECh. 5.3 - Prob. 6ECh. 5.3 - Prob. 7ECh. 5.3 - Prob. 8ECh. 5.3 - Prob. 9ECh. 5.3 - Prob. 10ECh. 5.3 - Prob. 11ECh. 5.3 - Prob. 12ECh. 5.3 - Prob. 13ECh. 5.3 - Prob. 14ECh. 5.3 - Prob. 15ECh. 5.3 - Prob. 16ECh. 5.3 - Prob. 17ECh. 5.3 - Prob. 18ECh. 5.3 - Prob. 19ECh. 5.3 - Prob. 20ECh. 5.3 - Prob. 21ECh. 5.3 - Prob. 22ECh. 5.3 - Prob. 23ECh. 5.3 - Prob. 24ECh. 5.3 - Prob. 25ECh. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - Prob. 28ECh. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - Prob. 31ECh. 5.3 - Prob. 32ECh. 5.3 - Prob. 33ECh. 5.3 - Prob. 34ECh. 5.3 - Prob. 35ECh. 5.3 - Prob. 36ECh. 5.3 - Prob. 37ECh. 5.3 - Prob. 38ECh. 5.3 - Prob. 39ECh. 5.3 - Prob. 40ECh. 5.3 - Prob. 41ECh. 5.3 - Prob. 42ECh. 5.4 - Prob. 1ECh. 5.4 - Prob. 2ECh. 5.4 - Prob. 3ECh. 5.4 - Prob. 4ECh. 5.4 - Prob. 5ECh. 5.4 - Prob. 6ECh. 5.4 - Prob. 7ECh. 5.4 - Prob. 8ECh. 5.4 - Prob. 9ECh. 5.4 - Prob. 10ECh. 5.4 - Prob. 11ECh. 5.4 - Prob. 12ECh. 5.4 - Prob. 13ECh. 5.4 - Prob. 14ECh. 5.4 - Prob. 15ECh. 5.4 - Prob. 16ECh. 5.4 - Prob. 17ECh. 5.4 - Prob. 18ECh. 5.4 - Prob. 19ECh. 5.4 - Prob. 20ECh. 5.4 - Prob. 21ECh. 5.4 - Prob. 22ECh. 5.4 - Prob. 23ECh. 5.4 - Prob. 24ECh. 5.4 - Prob. 25ECh. 5.4 - Prob. 26ECh. 5.4 - Prob. 27ECh. 5.4 - Prob. 28ECh. 5.4 - Prob. 29ECh. 5.4 - Prob. 30ECh. 5.4 - Prob. 31ECh. 5.4 - Prob. 32ECh. 5.4 - Prob. 33ECh. 5.4 - Prob. 34ECh. 5.4 - Prob. 35ECh. 5.4 - Prob. 36ECh. 5.4 - Prob. 1QCh. 5.4 - Prob. 2QCh. 5.4 - Prob. 3QCh. 5.4 - Prob. 4QCh. 5.4 - Prob. 5QCh. 5.4 - Prob. 6QCh. 5.4 - Prob. 7QCh. 5.4 - Prob. 8QCh. 5.4 - Prob. 9QCh. 5.4 - Prob. 10QCh. 5.4 - Prob. 11QCh. 5.4 - Prob. 12QCh. 5.4 - Prob. 13QCh. 5.4 - Prob. 14QCh. 5.4 - Prob. 15QCh. 5.5 - Prob. 1ECh. 5.5 - Prob. 2ECh. 5.5 - Prob. 3ECh. 5.5 - Prob. 4ECh. 5.5 - Prob. 5ECh. 5.5 - Prob. 6ECh. 5.5 - Prob. 7ECh. 5.5 - Prob. 8ECh. 5.5 - Prob. 9ECh. 5.5 - Prob. 10ECh. 5.5 - Prob. 11ECh. 5.5 - Prob. 12ECh. 5.5 - Prob. 13ECh. 5.5 - Prob. 14ECh. 5.5 - Prob. 15ECh. 5.5 - Prob. 16ECh. 5.5 - Prob. 17ECh. 5.5 - Prob. 18ECh. 5.5 - Prob. 19ECh. 5.5 - Prob. 20ECh. 5.5 - Prob. 21ECh. 5.5 - Prob. 22ECh. 5.5 - Prob. 23ECh. 5.5 - Prob. 24ECh. 5.5 - Prob. 25ECh. 5.5 - Prob. 26ECh. 5.5 - Prob. 27ECh. 5.5 - Prob. 28ECh. 5.5 - Prob. 29ECh. 5.5 - Prob. 30ECh. 5.5 - Prob. 31ECh. 5.5 - Prob. 32ECh. 5.5 - Prob. 33ECh. 5.5 - Prob. 34ECh. 5.5 - Prob. 35ECh. 5.5 - Prob. 36ECh. 5.5 - Prob. 37ECh. 5.5 - Prob. 38ECh. 5.5 - Prob. 39ECh. 5.5 - Prob. 40ECh. 5.5 - Prob. 41ECh. 5.5 - Prob. 42ECh. 5.5 - Prob. 43ECh. 5.5 - Prob. 44ECh. 5.5 - Prob. 45ECh. 5.5 - Prob. 46ECh. 5.5 - Prob. 47ECh. 5.5 - Prob. 48ECh. 5.5 - Prob. 49ECh. 5.6 - Prob. 1ECh. 5.6 - Prob. 2ECh. 5.6 - Prob. 3ECh. 5.6 - Prob. 4ECh. 5.6 - Prob. 5ECh. 5.6 - Prob. 6ECh. 5.6 - Prob. 7ECh. 5.6 - Prob. 8ECh. 5.6 - Prob. 9ECh. 5.6 - Prob. 10ECh. 5.6 - Prob. 11ECh. 5.6 - Prob. 12ECh. 5.6 - Prob. 13ECh. 5.6 - Prob. 14ECh. 5.6 - Prob. 15ECh. 5.6 - Prob. 16ECh. 5.6 - Prob. 17ECh. 5.6 - Prob. 18ECh. 5.6 - Prob. 19ECh. 5.6 - Prob. 20ECh. 5.6 - Prob. 21ECh. 5.6 - Prob. 22ECh. 5.6 - Prob. 23ECh. 5.6 - Prob. 24ECh. 5.6 - Prob. 25ECh. 5.6 - Prob. 26ECh. 5.6 - Prob. 27ECh. 5.6 - Prob. 28ECh. 5.6 - Prob. 29ECh. 5.6 - Prob. 30ECh. 5.6 - Prob. 31ECh. 5.6 - Prob. 32ECh. 5.6 - Prob. 33ECh. 5.6 - Prob. 34ECh. 5.6 - Prob. 35ECh. 5.6 - Prob. 36ECh. 5.6 - Prob. 37ECh. 5.6 - Prob. 38ECh. 5.6 - Prob. 39ECh. 5.6 - Prob. 40ECh. 5.6 - Prob. 41ECh. 5.6 - Prob. 42ECh. 5.6 - Prob. 43ECh. 5.6 - Prob. 44ECh. 5.6 - Prob. 45ECh. 5.6 - Prob. 46ECh. 5.6 - Prob. 47ECh. 5.6 - Prob. 48ECh. 5.7 - Prob. 1ECh. 5.7 - Prob. 2ECh. 5.7 - Prob. 3ECh. 5.7 - Prob. 4ECh. 5.7 - Prob. 5ECh. 5.7 - Prob. 6ECh. 5.7 - Prob. 7ECh. 5.7 - Prob. 8ECh. 5.7 - Prob. 9ECh. 5.7 - Prob. 10ECh. 5.7 - Prob. 11ECh. 5.7 - Prob. 12ECh. 5.7 - Prob. 13ECh. 5.7 - Prob. 14ECh. 5.7 - Prob. 15ECh. 5.7 - Prob. 16ECh. 5.7 - Prob. 17ECh. 5.7 - Prob. 18ECh. 5.7 - Prob. 19ECh. 5.7 - Prob. 20ECh. 5.7 - Prob. 21ECh. 5.7 - Prob. 22ECh. 5.7 - Prob. 23ECh. 5.7 - Prob. 24ECh. 5.7 - Prob. 25ECh. 5.7 - Prob. 26ECh. 5.7 - Prob. 27ECh. 5.7 - Prob. 28ECh. 5.7 - Prob. 29ECh. 5.7 - Prob. 30ECh. 5.7 - Prob. 31ECh. 5.7 - Prob. 32ECh. 5.7 - Prob. 33ECh. 5.7 - Prob. 34ECh. 5.7 - Prob. 35ECh. 5.7 - Prob. 36ECh. 5.7 - Prob. 37ECh. 5.7 - Prob. 38ECh. 5.7 - Prob. 39ECh. 5.7 - Prob. 40ECh. 5.7 - Prob. 41ECh. 5.7 - Prob. 42ECh. 5.7 - Prob. 43ECh. 5.7 - Prob. 44ECh. 5.7 - Prob. 45ECh. 5.7 - Prob. 46ECh. 5.7 - Prob. 47ECh. 5.7 - Prob. 48ECh. 5.7 - Prob. 49ECh. 5.7 - Prob. 50ECh. 5.7 - Prob. 51ECh. 5.7 - Prob. 52ECh. 5.7 - Prob. 53ECh. 5.7 - Prob. 54ECh. 5.7 - Prob. 55ECh. 5 - Prob. 1CRCh. 5 - Prob. 2CRCh. 5 - Prob. 3CRCh. 5 - Prob. 4CRCh. 5 - Prob. 5CRCh. 5 - Prob. 6CRCh. 5 - Prob. 7CRCh. 5 - Prob. 8CRCh. 5 - Prob. 9CRCh. 5 - Prob. 10CRCh. 5 - Prob. 11CRCh. 5 - Prob. 12CRCh. 5 - Prob. 13CRCh. 5 - Prob. 14CRCh. 5 - Prob. 15CRCh. 5 - Prob. 16CRCh. 5 - Prob. 17CRCh. 5 - Prob. 18CRCh. 5 - Prob. 19CRCh. 5 - Prob. 20CRCh. 5 - Prob. 21CRCh. 5 - Prob. 22CRCh. 5 - Prob. 1CTCh. 5 - Prob. 2CTCh. 5 - Prob. 3CTCh. 5 - Prob. 4CTCh. 5 - Prob. 5CTCh. 5 - Prob. 6CTCh. 5 - Prob. 7CTCh. 5 - Prob. 8CTCh. 5 - Prob. 9CTCh. 5 - Prob. 10CTCh. 5 - Prob. 11CTCh. 5 - Prob. 12CTCh. 5 - Prob. 13CTCh. 5 - Prob. 14CTCh. 5 - Prob. 15CTCh. 5 - Prob. 1CACh. 5 - Prob. 2CACh. 5 - Prob. 3CACh. 5 - Prob. 4CACh. 5 - Prob. 5CACh. 5 - Prob. 6CACh. 5 - Prob. 7CACh. 5 - Prob. 8CACh. 5 - Prob. 9CACh. 5 - Prob. 10CA
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- For each of the following series, determine whether the absolute convergence series test determines absolute convergence or fails. For the ¿th series, if the test is inconclusive then let Mi = 4, while if the test determines absolute convergence let Mi 1 : 2: ∞ Σ(−1)"+¹ sin(2n); n=1 Σ n=1 Σ ((−1)”. COS n² 3+2n4 3: (+ 4: 5 : n=1 ∞ n 2+5n3 ПП n² 2 5+2n3 пп n² Σ(+)+ n=1 ∞ n=1 COS 4 2 3+8n3 П ηπ n- (−1)+1 sin (+727) 5 + 2m³ 4 = 8. Then the value of cos(M₁) + cos(2M2) + cos(3M3) + sin(2M) + sin(M5) is -0.027 -0.621 -1.794 -1.132 -1.498 -4.355 -2.000 2.716arrow_forwardi need help with this question i tried by myself and so i am uploadding the question to be quided with step by step solution and please do not use chat gpt i am trying to learn thank you.arrow_forwardi need help with this question i tried by myself and so i am uploadding the question to be quided with step by step solution and please do not use chat gpt i am trying to learn thank you.arrow_forward
- Class, the class silues, and the class notes, whether the series does alternate and the absolute values of the terms decrease), and if the test does apply, determine whether the series converges or diverges. For the ith series, if the test does not apply the let Mi = 2, while if the test determines divergence then M¿ = 4, and if it determines convergence then M¿ = 8. 1: 2: 3 : 4: 5 : ∞ n=1 ∞ (−1)n+1. Σ(-1) +1 n=1 ∞ п 3m² +2 Σ(-1)+1 sin(2n). n=1 ∞ 2n² + 2n +3 4n2 +6 1 e-n + n² 3n23n+1 9n² +3 In(n + 1) 2n+1 Σ(-1) +1 n=1 ∞ Σ(-1)". n=1 Then the value of cos(M₁) + cos(2M2) + cos(3M3) + sin(2M4) + sin(M5) is 1.715 0.902 0.930 -1.647 -0.057 ● 2.013 1.141 4.274arrow_forward3. FCX14) = x²+3xx-y3 +.arrow_forwardBH is tangent to circle A and DF is a diameter. I don't know where to go from here. May you help please?arrow_forward
- A cylindrical chemical storage tank with a capacity of 950m3 is going to be constructed in a warehouse that is 11m by 14m with a height of 10m. The specifications call for the case to be made of sheet metal that costs $90/m2, the top to be made from sheet metal that costs $45/m2 and the wall to be made of sheet metal that costs $80/m2. If you want to minimize the cost to make the storage house, how much would you end up spending to build the tank?arrow_forwardCalculate the max value of the directional derivatearrow_forwardselect bmw stock. you can assume the price of the stockarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
UG/ linear equation in linear algebra; Author: The Gate Academy;https://www.youtube.com/watch?v=aN5ezoOXX5A;License: Standard YouTube License, CC-BY
System of Linear Equations-I; Author: IIT Roorkee July 2018;https://www.youtube.com/watch?v=HOXWRNuH3BE;License: Standard YouTube License, CC-BY