Chapter 54, Problem 22A

Solve the following exercises based on Principles 18 through 21, although an exercise may require the application oftwo or more of any of the principles. Where necessary, round linear answers in inches to 3 decimal places and millimeters to 2 decimal places. Round angular answers in decimal degrees to 2 decimal places and degrees and minutes to the nearest minute.

a. If $\stackrel{⌢}{AB}=72°18\text{'}$ and $\stackrel{⌢}{CD}=50°24\text{'}$ find:
(1) ∠1
(2) ∠2
(3) ∠3
b. If $\stackrel{⌢}{CD}=43°15\text{'}$ and $\stackrel{⌢}{AD}=106°05\text{'}$ , find:
(1) ∠1
(2) ∠2
(3) ∠3

To determine

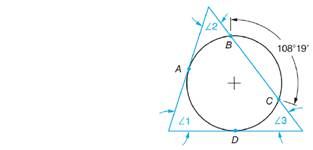
(a)

The values of angles $\angle 1,\angle 2\text{and }\angle 3$

Answer to Problem 22A

The values of angles are

  $\angle 1=50°57\text{'}$

  $\angle 2=53°30\text{'}$

  $\angle 3=75°32\text{'}$

Explanation of Solution

Given information:

  $\begin{array}{l}\stackrel{⌢}{AB}=72°20\text{'}\\ \stackrel{⌢}{CD}=50°18\text{'}\end{array}$

Given figure is

Calculation:

The angle which is formed at a point on outside a circle by two tangents, two secants or a secant and a tangent is equal to one half the difference of arcs intercepted by the tangents or secants.

Let us first calculate the value of arc AD,

The total angle subtended by the entire circular arc on the center is 360^o.

  $\begin{array}{l}\stackrel{⌢}{AD}+\stackrel{⌢}{DC}+\stackrel{⌢}{BC}+\stackrel{⌢}{AB}=360°\\ \stackrel{⌢}{AD}+50°18\text{'}+108°19\text{'}+72°20\text{'}=360°\\ \stackrel{⌢}{AD}=360°-\left(50°18\text{'}+108°19\text{'}+72°20\text{'}\right)\end{array}$

  $\stackrel{⌢}{AD}=129°3\text{'}$

Now,

  $\begin{array}{l}\angle 1=\frac{1}{2}\left(\stackrel{⌢}{ABCD}-\stackrel{⌢}{AD}\right)\\ \text{Putting the given values}\\ \angle 1=\frac{1}{2}\left(\left(50°18\text{'}+108°19\text{'}+72°20\text{'}\right)-\stackrel{⌢}{129°3\text{'}}\right)\\ \angle 1=\frac{1}{2}\left(\left(230°57\text{'}\right)-129°3\text{'}\right)\\ \angle 1=\frac{1}{2}\times \left(101°54\text{'}\right)\end{array}$

  $\angle 1=50°57\text{'}$

Now, for calculating angle 2,

Similarly,

  $\begin{array}{l}\angle 2=\frac{1}{2}\left(\stackrel{⌢}{ADC}-\stackrel{⌢}{AB}\right)\\ \text{Putting the given values}\\ \angle 2=\frac{1}{2}\left(\left(\stackrel{⌢}{AD}+\stackrel{⌢}{DC}\right)-\stackrel{⌢}{AB}\right)\\ \angle 2=\frac{1}{2}\left(\left(129°3\text{'}\right)+50°18\text{'}\right)-72°20\text{'}\\ \angle 2=\frac{1}{2}\times 107°1\text{'}\end{array}$

  $\angle 2=53°30\text{'}$

Now, for calculating angle 3,

Similarly,

  $\begin{array}{l}\angle 3=\frac{1}{2}\left(\stackrel{⌢}{DAB}-\stackrel{⌢}{DC}\right)\\ \text{Putting the given values}\\ \angle 3=\frac{1}{2}\left(\left(\stackrel{⌢}{AD}+\stackrel{⌢}{AB}\right)-\stackrel{⌢}{DC}\right)\\ \angle 3=\frac{1}{2}\left(\left(129°3\text{'}\right)+72°20\text{'}\right)-50°18\text{'}\end{array}$

  $\angle 3=75°32\text{'}$

Conclusion:

Thus, the values of angles are

  $\angle 1=50°57\text{'}$

  $\angle 2=53°30\text{'}$

  $\angle 3=75°32\text{'}$

To determine

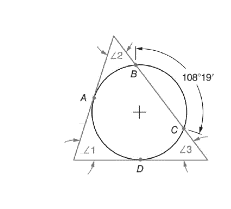
(b)

The values of angles $\angle 1,\angle 2\text{and }\angle 3$

Answer to Problem 22A

The values of angles are

  $\angle 1=73°55\text{'}$

  $\angle 2=23°30\text{'}$

  $\angle 3=82°36\text{'}$

Explanation of Solution

Given information:

  $\begin{array}{l}\stackrel{⌢}{AD}=106°05\text{'}\\ \stackrel{⌢}{CD}=43°15\text{'}\end{array}$

Given figure is

Calculation:

The angle which is formed at a point on outside a circle by two tangents, two secants or a secant and a tangent is equal to one half the difference of arcs intercepted by the tangents or secants.

Let us first calculate the value of arc AB,

The total angle subtended by the entire circular arc on the center is 360^o.

  $\begin{array}{l}\stackrel{⌢}{AD}+\stackrel{⌢}{DC}+\stackrel{⌢}{BC}+\stackrel{⌢}{AB}=360°\\ 106°05\text{'}+43°15\text{'}+108°19\text{'}+\stackrel{⌢}{AB}=360°\\ \stackrel{⌢}{AB}=360°-\left(106°05\text{'}+43°15\text{'}+108°19\text{'}\right)\\ \stackrel{⌢}{AB}=360°-257°39\text{'}\end{array}$

  $\stackrel{⌢}{AB}=102°21\text{'}$

Now,

  $\begin{array}{l}\angle 1=\frac{1}{2}\left(\stackrel{⌢}{ABCD}-\stackrel{⌢}{AD}\right)\\ \text{Putting the given values}\\ \angle 1=\frac{1}{2}\left(\left(102°21\text{'}+108°19\text{'}+43°15\text{'}\right)-106°05\text{'}\right)\\ \angle 1=\frac{1}{2}\left(\left(253°55\text{'}\right)-106°05\text{'}\right)\\ \angle 1=\frac{1}{2}\times \left(147°50\text{'}\right)\end{array}$

  $\angle 1=73°55\text{'}$

Now, for calculating angle 2,

Similarly,

  $\begin{array}{l}\angle 2=\frac{1}{2}\left(\stackrel{⌢}{ADC}-\stackrel{⌢}{AB}\right)\\ \text{Putting the given values}\\ \angle 2=\frac{1}{2}\left(\left(\stackrel{⌢}{AD}+\stackrel{⌢}{DC}\right)-\stackrel{⌢}{AB}\right)\\ \angle 2=\frac{1}{2}\left(\left(106°05\text{'}\right)+43°15\text{'}\right)-102°21\text{'}\\ \angle 2=\frac{1}{2}\times 46°59\text{'}\end{array}$

  $\angle 2=23°30\text{'}$

Now, for calculating angle 3,

Similarly,

  $\begin{array}{l}\angle 3=\frac{1}{2}\left(\stackrel{⌢}{DAB}-\stackrel{⌢}{DC}\right)\\ \text{Putting the given values}\\ \angle 3=\frac{1}{2}\left(\left(\stackrel{⌢}{AD}+\stackrel{⌢}{AB}\right)-\stackrel{⌢}{DC}\right)\\ \angle 3=\frac{1}{2}\left(\left(106°05\text{'}\right)+102°21\text{'}\right)-43°15\text{'}\\ \angle 3=\frac{1}{2}\times 165°11\text{'}\end{array}$

  $\angle 3=82°36\text{'}$

Conclusion:

Thus, the values of angles are

  $\angle 1=73°55\text{'}$

  $\angle 2=23°30\text{'}$

  $\angle 3=82°36\text{'}$