Chapter 54, Problem 20A

Solve the following exercises based on Principles 18 through 21, although an exercise may require the application oftwo or more of any of the principles. Where necessary, round linear answers in inches to 3 decimal places and millimeters to 2 decimal places. Round angular answers in decimal degrees to 2 decimal places and degrees and minutes to the nearest minute.

a. If $\stackrel{⌢}{EF}=84°$, find
(1) ∠EFD
(2) $\stackrel{⌢}{HF}$
(3) ∠1
b. If $\stackrel{⌢}{EF}=79°$, find
(1) ∠EFD
(2) $\stackrel{⌢}{HF}$
(3) ∠1

To determine

(a)

The value of $\angle EFD,\stackrel{⌢}{HF},\text{and }\angle \text{1}$ in the given figure.

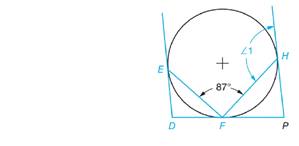
Answer to Problem 20A

The value of $\angle EFD,\stackrel{⌢}{HF},\text{and }\angle \text{1}$ are

  $\stackrel{⌢}{DC}=76.00°$

  $\angle EOD=31.00°$

  $\stackrel{⌢}{AC}=134.00°$

Explanation of Solution

Given information:

  $\stackrel{⌢}{EF}=84°$

The given figure is

  

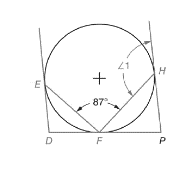
Calculation:

The angle drawn at the point of tangent between the tangent and the chord is equal to half the value of intercepted arc.

The angle EFD, is the angle between the tangent DF and the chord EF, thus, the value of angle EFD will be equal to

  $\begin{array}{l}\angle EFD=\frac{\stackrel{⌢}{EF}}{2}\\ \angle EFD=\frac{84°}{2}=42°\\ \angle EFD=42°\end{array}$

The line DFP is the straight line, the angle at the straight line is 180^o. The value of angle FHP is to be calculated for calculating the value of arc HF.

  $\begin{array}{l}\angle EFD+\angle EFH+\angle HFP=180°\\ 42°+87°+\angle HFP=180°\\ \angle HFP=180°-\left(42°+87°\right)\\ \angle HFP=58°\end{array}$

The angle drawn at the point of tangent between the tangent and the chord is equal to half the value of intercepted arc. So,

  $\begin{array}{l}\angle HFP=\frac{\stackrel{⌢}{HF}}{2}\\ \stackrel{⌢}{HF}=2\times \angle HFP\\ \stackrel{⌢}{HF}=2\times 58°\\ \stackrel{⌢}{HF}=116°\end{array}$

To calculate the value of angle 1, let us first calculate the value of arc FEH.

  $\begin{array}{l}\stackrel{⌢}{EH}=360°-\left(79°+116°\right)\\ \stackrel{⌢}{EH}=165°\\ \stackrel{⌢}{FEH}=\stackrel{⌢}{FE}+\stackrel{⌢}{EH}\\ \stackrel{⌢}{FEH}=79°+165°\\ \stackrel{⌢}{FEH}=244°\end{array}$

Similarly, for angle 1, the angle drawn at the point of tangent between the tangent and the chord is equal to half the value of intercepted arc.

  $\begin{array}{l}\angle 1=\frac{\stackrel{⌢}{FEH}}{2}\\ \angle 1=\frac{244°}{2}\\ \angle 1=122°\end{array}$

Conclusion:

Thus, the value of $\angle EFD\text{,}\stackrel{⌢}{HF}\text{and }\angle \text{1}$ are

  $\angle EFD=42°$

  $\stackrel{⌢}{HF}=116°$

  $\angle 1=122°$

To determine

(b)

The value of $\angle EFD,\stackrel{⌢}{HF},\text{and }\angle \text{1}$ in the given figure.

Answer to Problem 20A

The value of $\angle EFD,\stackrel{⌢}{HF},\text{and }\angle \text{1}$ are

  $\stackrel{⌢}{DC}=76.00°$

  $\angle EOD=31.00°$

  $\stackrel{⌢}{AC}=134.00°$

Explanation of Solution

Given information:

  $\stackrel{⌢}{EF}=84°$

The given figure is

  

Calculation:

The angle drawn at the point of tangent between the tangent and the chord is equal to half the value of intercepted arc.

The angle EFD, is the angle between the tangent DF and the chord EF, thus, the value of angle EFD will be equal to

  $\begin{array}{l}\angle EFD=\frac{\stackrel{⌢}{EF}}{2}\\ \angle EFD=\frac{84°}{2}=42°\\ \angle EFD=42°\end{array}$

The line DFP is the straight line, the angle at the straight line is 180^o. The value of angle FHP is to be calculated for calculating the value of arc HF.

  $\begin{array}{l}\angle EFD+\angle EFH+\angle HFP=180°\\ 42°+87°+\angle HFP=180°\\ \angle HFP=180°-\left(42°+87°\right)\\ \angle HFP=58°\end{array}$

The angle drawn at the point of tangent between the tangent and the chord is equal to half the value of intercepted arc. So,

  $\begin{array}{l}\angle HFP=\frac{\stackrel{⌢}{HF}}{2}\\ \stackrel{⌢}{HF}=2\times \angle HFP\\ \stackrel{⌢}{HF}=2\times 58°\\ \stackrel{⌢}{HF}=116°\end{array}$

To calculate the value of angle 1, let us first calculate the value of arc FEH.

  $\begin{array}{l}\stackrel{⌢}{EH}=360°-\left(79°+116°\right)\\ \stackrel{⌢}{EH}=165°\\ \stackrel{⌢}{FEH}=\stackrel{⌢}{FE}+\stackrel{⌢}{EH}\\ \stackrel{⌢}{FEH}=79°+165°\\ \stackrel{⌢}{FEH}=244°\end{array}$

Similarly, for angle 1, the angle drawn at the point of tangent between the tangent and the chord is equal to half the value of intercepted arc.

  $\begin{array}{l}\angle 1=\frac{\stackrel{⌢}{FEH}}{2}\\ \angle 1=\frac{244°}{2}\\ \angle 1=122°\end{array}$

Conclusion:

Thus, the value of $\angle EFD\text{,}\stackrel{⌢}{HF}\text{and }\angle \text{1}$ are

  $\angle EFD=42°$

  $\stackrel{⌢}{HF}=116°$

  $\angle 1=122°$