Chapter 5.4, Problem 19E

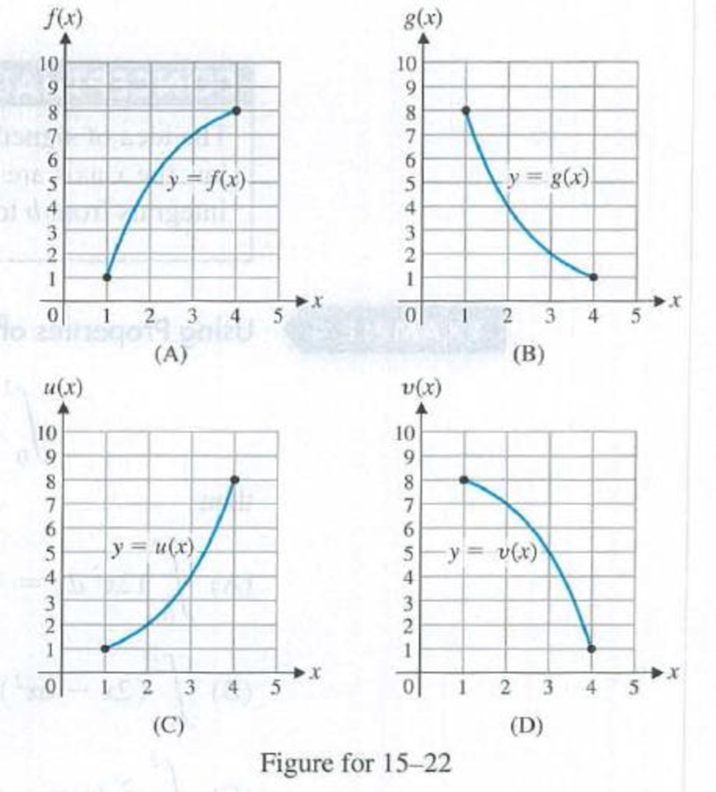
Problems 15–22 involve estimating the area under the curves in Figures A–D from x = 1 to x = 4. For each figure, divide the interval [1, 4] into three equal subintervals.

19. Replace the question marks with L₃ and R₃ as appropriate. Explain your choice.

$\begin{array}{cc}?\le {\displaystyle \underset{1}{\overset{4}{\int }}f\left(x\right)}dx\le ?& ?\le {\displaystyle \underset{1}{\overset{4}{\int }}g\left(x\right)}dx\le ?\end{array}$