Finite Mathematics for Business, Economics, Life Sciences and Social Sciences Plus NEW MyLab Math with Pearson eText -- Access Card Package (13th Edition)
13th Edition
ISBN: 9780321947628
Author: Raymond A. Barnett, Michael R. Ziegler, Karl E. Byleen
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5.3, Problem 49E
In Problems 49-64, construct a mathematical model in the form of a linear programming problem. (The answers in the back of the book for these application problems include the model.) Then solve by the geometric method.
Fertilizer. A fruit grower can use two types of fertilizer in his orange grove, brand
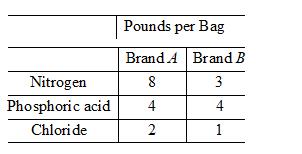
(A) If the grower wants to maximize the amount of nitrogen added to the grove, how many bags of each mix should be used? How much nitrogen will be added?
(B) If the grower wants to minimize the amount of nitrogen added to the grove, how many bags of each mix should be used? How much nitrogen will be added?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Refer to page 140 for problems on infinite sets.
Instructions:
• Compare the cardinalities of given sets and classify them as finite, countable, or uncountable.
•
Prove or disprove the equivalence of two sets using bijections.
• Discuss the implications of Cantor's theorem on real-world computation.
Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]
Refer to page 120 for problems on numerical computation.
Instructions:
• Analyze the sources of error in a given numerical method (e.g., round-off, truncation).
• Compute the error bounds for approximating the solution of an equation.
•
Discuss strategies to minimize error in iterative methods like Newton-Raphson.
Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]
Refer to page 145 for problems on constrained optimization.
Instructions:
•
Solve an optimization problem with constraints using the method of Lagrange multipliers.
•
•
Interpret the significance of the Lagrange multipliers in the given context.
Discuss the applications of this method in machine learning or operations research.
Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]
Chapter 5 Solutions
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences Plus NEW MyLab Math with Pearson eText -- Access Card Package (13th Edition)
Ch. 5.1 - Graph 6x3y18.Ch. 5.1 - Graph (A) y4 (B) 4x9 (C) 3x2yCh. 5.1 - Find the linear inequality whose graph is given in...Ch. 5.1 - A food vendor at a rock concert sells hot dogs for...Ch. 5.1 - For Problems 1-8, if necessary, review Section...Ch. 5.1 - For Problems 1-8, if necessary, review Section...Ch. 5.1 - For Problems 1-8, if necessary, review Section...Ch. 5.1 - For Problems 1-8, if necessary, review Section...Ch. 5.1 - For Problems 1-8, if necessary, review Section...Ch. 5.1 - For Problems 1-8, if necessary, review Section...
Ch. 5.1 - For Problems 1-8, if necessary, review Section...Ch. 5.1 - For Problems 1-8, if necessary, review Section...Ch. 5.1 - Graph each inequality in Problems 9-18. yx1Ch. 5.1 - Graph each inequality in Problems 9-18. yx+1Ch. 5.1 - Graph each inequality in Problems 9-18. 3x2y6Ch. 5.1 - Graph each inequality in Problems 9-18. 2x5y10Ch. 5.1 - Graph each inequality in Problems 9-18. x4Ch. 5.1 - Graph each inequality in Problems 9-18. y5Ch. 5.1 - Graph each inequality in Problems 9-18. 6x+4y24Ch. 5.1 - Graph each inequality in Problems 9-18. 4x+8y32Ch. 5.1 - Graph each inequality in Problems 9-18. 5x2yCh. 5.1 - Graph each inequality in Problems 9-18. 6x4yCh. 5.1 - In Problems 19-22, (A) graph the set of points...Ch. 5.1 - In Problems 19-22, (A) graph the set of points...Ch. 5.1 - In Problems 19-22, (A) graph the set of points...Ch. 5.1 - In Problems 19-22, (A) graph the set of points...Ch. 5.1 - In Problems 23-28, define the variable and...Ch. 5.1 - In Problems 23-28, define the variable and...Ch. 5.1 - In Problems 23-28, define the variable and...Ch. 5.1 - In Problems 23-28, define the variable and...Ch. 5.1 - In Problems 23-28, define the variable and...Ch. 5.1 - In Problems 23-28, define the variable and...Ch. 5.1 - In Exercises 33-38, state the linear inequality...Ch. 5.1 - In Exercises 33-38, state the linear inequality...Ch. 5.1 - In Exercises 33-38, state the linear inequality...Ch. 5.1 - In Exercises 33-38, state the linear inequality...Ch. 5.1 - In Exercises 33-38, state the linear inequality...Ch. 5.1 - In Exercises 33-38, state the linear inequality...Ch. 5.1 - In Problems 39-44, define two variables and...Ch. 5.1 - In Problems 39-44, define two variables and...Ch. 5.1 - In Problems 39-44, define two variables and...Ch. 5.1 - In Problems 39-44, define two variables and...Ch. 5.1 - In Problems 39-44, define two variables and...Ch. 5.1 - In Problems 39-44, define two variables and...Ch. 5.1 - In Problems 45-54, graph each inequality subject...Ch. 5.1 - In Problems 45-54, graph each inequality subject...Ch. 5.1 - In Problems 45-54, graph each inequality subject...Ch. 5.1 - In Problems 45-54, graph each inequality subject...Ch. 5.1 - In Problems 45-54, graph each inequality subject...Ch. 5.1 - In Problems 45-54, graph each inequality subject...Ch. 5.1 - In Problems 45-54, graph each inequality subject...Ch. 5.1 - In Problems 45-54, graph each inequality subject...Ch. 5.1 - In Problems 45-54, graph each inequality subject...Ch. 5.1 - In Problems 45-54, graph each inequality subject...Ch. 5.1 - In Problems 51-62, express your answer as a linear...Ch. 5.1 - Prob. 52ECh. 5.1 - In Problems 55-66, express your answer as a linear...Ch. 5.1 - In Problems 55-66, express your answer as a linear...Ch. 5.1 - In Problems 55-66, express your answer as a linear...Ch. 5.1 - In Problems 55-66, express your answer as a linear...Ch. 5.1 - In Problems 55-66, express your answer as a linear...Ch. 5.1 - In Problems 55-66, express your answer as a linear...Ch. 5.1 - In Problems 55-66, express your answer as a linear...Ch. 5.1 - In Problems 55-66, express your answer as a linear...Ch. 5.1 - In Problems 55-66, express your answer as a linear...Ch. 5.1 - In Problems 55-66, express your answer as a linear...Ch. 5.2 - Solve the following system of linear inequalities...Ch. 5.2 - Solve the following system of linear inequalities...Ch. 5.2 - A manufacturing plant makes two types of...Ch. 5.2 - For Problems 1-8, if necessary, review Section...Ch. 5.2 - For Problems 1-8, if necessary, review Section...Ch. 5.2 - For Problems 1-8, if necessary, review Section...Ch. 5.2 - For Problems 1-8, if necessary, review Section...Ch. 5.2 - For Problems 1-8, if necessary, review Section...Ch. 5.2 - For Problems 1-8, if necessary, review Section...Ch. 5.2 - For Problems 1-8, if necessary, review Section...Ch. 5.2 - For Problems 1-8, if necessary, review Section...Ch. 5.2 - In Problems 9-12, match the solution region of...Ch. 5.2 - In Problems 9-12, match the solution region of...Ch. 5.2 - In Problems 9-12, match the solution region of...Ch. 5.2 - In Problems 9-12, match the solution region of...Ch. 5.2 - In Problems 13-16, solve each system of linear...Ch. 5.2 - In Problems 13-16, solve each system of linear...Ch. 5.2 - In Problems 13-16, solve each system of linear...Ch. 5.2 - In Problems 13-16, solve each system of linear...Ch. 5.2 - In Problems 17-20, match the solution region of...Ch. 5.2 - In Problems 17-20, match the solution region of...Ch. 5.2 - In Problems 17-20, match the solution region of...Ch. 5.2 - In Problems 17-20, match the solution region of...Ch. 5.2 - Solve the systems in Problems 29-38 graphically...Ch. 5.2 - Solve the systems in Problems 29-38 graphically...Ch. 5.2 - Solve the systems in Problems 29-38 graphically...Ch. 5.2 - Solve the systems in Problems 29-38 graphically...Ch. 5.2 - Solve the systems in Problems 29-38 graphically...Ch. 5.2 - Solve the systems in Problems 29-38 graphically...Ch. 5.2 - Solve the systems in Problems 29-38 graphically...Ch. 5.2 - Solve the systems in Problems 29-38 graphically...Ch. 5.2 - Solve the systems in Problems 29-38 graphically...Ch. 5.2 - Solve the systems in Problems 29-38 graphically...Ch. 5.2 - Solve the systems in Problems 39-48 graphically...Ch. 5.2 - Solve the systems in Problems 39-48 graphically...Ch. 5.2 - Solve the systems in Problems 39-48 graphically...Ch. 5.2 - \ Solve the systems in Problems 39-48 graphically...Ch. 5.2 - Solve the systems in Problems 39-48 graphically...Ch. 5.2 - Solve the systems in Problems 39-48 graphically...Ch. 5.2 - Solve the systems in Problems 39-48 graphically...Ch. 5.2 - Solve the systems in Problems 39-48 graphically...Ch. 5.2 - Solve the systems in Problems 39-48 graphically...Ch. 5.2 - Solve the systems in Problems 39-48 graphically...Ch. 5.2 - Problems 49 and 50 introduce an algebraic process...Ch. 5.2 - Problems 49 and 50 introduce an algebraic process...Ch. 5.2 - Water skis. A manufacturing company makes two...Ch. 5.2 - Furniture. A furniture manufacturing company...Ch. 5.2 - Water skis. Refer to Problem 51. The company makes...Ch. 5.2 - Furniture. Refer to Problem 52. The company makes...Ch. 5.2 - Plant food. A farmer can buy two types of plant...Ch. 5.2 - Nutrition. A dietician in a hospital is to arrange...Ch. 5.2 - Psychology. A psychologist uses two types of boxes...Ch. 5.3 - A manufacturing plant makes two types of...Ch. 5.3 - Refer to the feasible region S shown in Figure 3....Ch. 5.3 - In Example 2B we saw that there was no optimal...Ch. 5.3 - (A) Maximize and minimize z=4x+2y subject to the...Ch. 5.3 - A chicken farmer can buy a special food mix A at...Ch. 5.3 - In Problem 1-8, if necessary, review Theorem 1. In...Ch. 5.3 - In Problem 1-8, if necessary, review Theorem 1. In...Ch. 5.3 - In Problem 1-8, if necessary, review Theorem 1. In...Ch. 5.3 - In Problem 1-8, if necessary, review Theorem 1. In...Ch. 5.3 - In Problems 1-8, if necessary, review Theorem 1....Ch. 5.3 - In Problems 1-8, if necessary, review Theorem 1....Ch. 5.3 - In Problems 1-8, if necessary, review Theorem 1....Ch. 5.3 - In Problems 1-8, if necessary, review Theorem 1....Ch. 5.3 - In Problems 9-12, graph the constant-profit lines...Ch. 5.3 - In Problems 9-12, graph the constant-profit lines...Ch. 5.3 - In Problems 9-12, graph the constant-profit lines...Ch. 5.3 - In Problems 9-12, graph the constant-profit lines...Ch. 5.3 - In Problems 13-16, graph the constant-cost lines...Ch. 5.3 - In Problems 13-16, graph the constant-cost lines...Ch. 5.3 - In Problems 13-16, graph the constant-cost lines...Ch. 5.3 - In Problems 13-16, graph the constant-cost lines...Ch. 5.3 - Solve the linear programming problems stated in...Ch. 5.3 - Solve the linear programming problems stated in...Ch. 5.3 - Solve the linear programming problems stated in...Ch. 5.3 - Solve the linear programming problems stated in...Ch. 5.3 - Solve the linear programming problems stated in...Ch. 5.3 - Solve the linear programming problems stated in...Ch. 5.3 - Prob. 23ECh. 5.3 - Solve the linear programming problems stated in...Ch. 5.3 - Solve the linear programming problems stated in...Ch. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - Solve the linear programming problems stated in...Ch. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - Solve the linear programming problems stated in...Ch. 5.3 - Prob. 32ECh. 5.3 - Solve the linear programming problems stated in...Ch. 5.3 - Solve the linear programming problems stated in...Ch. 5.3 - In Problems 39 and 40, explain why Theorem 2...Ch. 5.3 - In Problems 39 and 40, explain why Theorem 2...Ch. 5.3 - The corner points for the bounded feasible region...Ch. 5.3 - Prob. 38ECh. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5.3 - In Problems 49-64, construct a mathematical model...Ch. 5 - Graph each inequality. x2y3Ch. 5 - Graph each inequality. 3y5x30Ch. 5 - Graph the systems in Problems 3-6 and indicate...Ch. 5 - Graph the systems in Problems 3-6 and indicate...Ch. 5 - Graph the systems in Problems 3-6 and indicate...Ch. 5 - Graph the systems in Problems 3-6 and indicate...Ch. 5 - In Exercises 7 and 8, state the linear inequality...Ch. 5 - In Exercises 7 and 8, state the linear inequality...Ch. 5 - Solve the linear programming problems in Problems...Ch. 5 - Solve the linear programming problems in Problems...Ch. 5 - Solve the linear programming problems in Problems...Ch. 5 - Solve the linear programming problems in Problems...Ch. 5 - Solve the linear programming problems in Problems...Ch. 5 - Electronics. A company uses two machines to solder...Ch. 5 - In problems 15 and 16, construct a mathematical...Ch. 5 - In problems 15 and 16, construct a mathematical...
Additional Math Textbook Solutions
Find more solutions based on key concepts
The table by using the given graph of h.
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
CHECK POINT I Express as a percent.
Thinking Mathematically (6th Edition)
Assessment 1-1A The following is a magic square all rows, columns, and diagonals sum to the same number. Find t...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
The following set of data is from sample of n=5: a. Compute the mean, median, and mode. b. Compute the range, v...
Basic Business Statistics, Student Value Edition
Fill in each blank so that the resulting statement is true. If n is a counting number, bn, read ______, indicat...
College Algebra (7th Edition)
The length of Amazon River in miles.
Pre-Algebra Student Edition
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Only 100% sure experts solve it correct complete solutions okarrow_forwardGive an example of a graph with at least 3 vertices that has exactly 2 automorphisms(one of which is necessarily the identity automorphism). Prove that your example iscorrect.arrow_forward3. [10 marks] Let Go (Vo, Eo) and G₁ = (V1, E1) be two graphs that ⚫ have at least 2 vertices each, ⚫are disjoint (i.e., Von V₁ = 0), ⚫ and are both Eulerian. Consider connecting Go and G₁ by adding a set of new edges F, where each new edge has one end in Vo and the other end in V₁. (a) Is it possible to add a set of edges F of the form (x, y) with x € Vo and y = V₁ so that the resulting graph (VUV₁, Eo UE₁ UF) is Eulerian? (b) If so, what is the size of the smallest possible F? Prove that your answers are correct.arrow_forward
- Let T be a tree. Prove that if T has a vertex of degree k, then T has at least k leaves.arrow_forwardHomework Let X1, X2, Xn be a random sample from f(x;0) where f(x; 0) = (-), 0 < x < ∞,0 € R Using Basu's theorem, show that Y = min{X} and Z =Σ(XY) are indep. -arrow_forwardHomework Let X1, X2, Xn be a random sample from f(x; 0) where f(x; 0) = e−(2-0), 0 < x < ∞,0 € R Using Basu's theorem, show that Y = min{X} and Z =Σ(XY) are indep.arrow_forward
- rmine the immediate settlement for points A and B shown in figure below knowing that Aq,-200kN/m², E-20000kN/m², u=0.5, Depth of foundation (DF-0), thickness of layer below footing (H)=20m. 4m B 2m 2m A 2m + 2m 4marrow_forwardSolve this pleasearrow_forward5.10. Discuss the continuity of the function f(z) = at the points 1, -1, i, and -i. 之一 21 3, |2 = 1arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Intermediate Algebra
Algebra
ISBN:9781285195728
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY