Chapter 5.2, Problem 5.44P

5.43 and 5.44

Determine by direct integration the centroid of the area shown. Express your answer in terms of a and b.

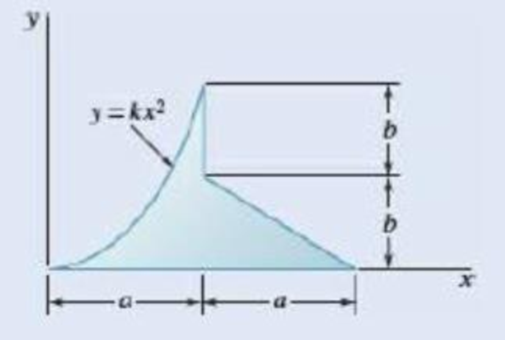
Fig. P5.44

To determine

The centroid of shaded area in Fig. P5.44 by method of direct integration.

Answer to Problem 5.44P

Centroid is located at $\left(a,\frac{17}{35}b\right)$.

Explanation of Solution

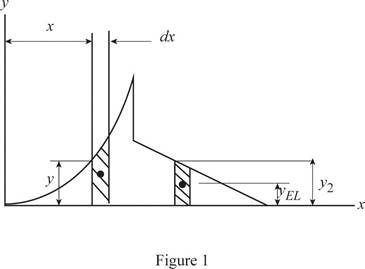
Refer the figure P5.44 and figure given below.

Write the equation for curve $y$.

$y=k{x}^2$ (I)

Here, $y$ is the y co-ordinate, $x$ is the x-coordinate, and $k$ is an unknown constant.

Consider the point $\left(a,2b\right)$.

Here, $a$ is a length on x-axis and $b$  is a length parallel to y axis.

Rewrite equation (I) by substituting $a$ for $x$ and $2b$ for $y$.

$2b=k{a}^2$

Rewrite the above equation in terms of $k$.

$k=\frac{2b}{a^2}$

Rewrite equation (I) by substituting the above relation for $k$.

$y=\frac{2b}{a^2}{x}^2$

Divide the shaded region in P5.44 into two parts for the purpose of integration. Region $0\le x\le a$ and   $a\le x\le 2a$.

Consider the region $0\le x\le a$ in P5.44.

Consider a rectangular differential area element in the region. Write the expression for the x-coordinate of center of mass of differential area element.

${\overline{x}}_{EL1}=x$

Here, ${\overline{x}}_{EL1}$ is the center of mass of differential area element in region $0\le x\le a$.

Write the expression for the y-coordinate of center of mass of differential area element in region $0\le x\le a$ in P5.43.

${\overline{y}}_{EL1}=\frac{y}{2}$

Here, ${\overline{y}}_{E{L}_1}$ is the y-coordinate of differential area element

Rewrite the above relation by substituting $\frac{2b}{a^2}{x}^2$ for $y$ in the above equation.

$\begin{array}{c}{\overline{y}}_{EL1}=\frac{1}{2}\left(\frac{2b}{a^2}{x}^2\right)\\ =\frac{b}{a^2}{x}^2\end{array}$ (II)

Write the expression to calculate the differential area element in $0\le x\le a$.

$d{A}_1=ydx$

Here, $d{A}_1$ is the differential area element in $0\le x\le a$ and $dx$ denotes a small change in $x$.

Rewrite the above relation by substituting $\frac{2b}{a^2}{x}^2$ for $y$ in the above equation.

$d{A}_1=\frac{2b}{a^2}{x}^{2}dx$ (III)

Consider the region $a\le x\le 2a$ in in P5.44.

Write the expression for the x-coordinate of center of mass of differential area element in region $a\le x\le 2a$.

${\overline{x}}_{EL2}=x$

Here, ${\overline{x}}_{EL2}$ is the center of mass of differential area element in region $a\le x\le 2a$

Write the expression for the y-coordinate of center of mass of differential area element in region $a\le x\le 2a$.

${\overline{y}}_{EL2}=\frac{y_2}{2}$ (IV)

Here, ${\overline{y}}_{EL2}$ is the y-coordinate of center of mass of differential area element in region $a\le x\le 2a$ and $y_2$ is a straight line in region $a\le x\le 2a$.

Calculate the slope of $y_2$ using points $\left(a,b\right)$ and $\left(2a,0\right)$.

$\begin{array}{c}m=\frac{0-b}{2a-a}\\ =-\frac{b}{a}\end{array}$

Here, $m$ is the slope of $y_2$.

Write the equation of $y_2$ using slope-point form of equation for straight line. Use the point $\left(2a,0\right)$ for finding the equation.

$y_2-0=m\left(x-2a\right)$

Rewrite the above equation by substituting $-\frac{b}{a}$ for $m$ to find $y_2$.

$\begin{array}{c}{y}_2=-\frac{b}{a}\left(x-2a\right)\\ =b\left(2-\frac{x}{a}\right)\end{array}$

Rewrite equation (IV) by substituting $b\left(2-\frac{x}{a}\right)$ for $y_2$.

${\overline{y}}_{EL2}=\frac{b}{2}\left(2-\frac{x}{a}\right)$ (V)

Write the expression for $d{A}_2$.

$d{A}_2=y_{2}dx$

Rewrite the above relation by substituting $b\left(2-\frac{x}{a}\right)$  for $y_2$.

$d{A}_2=b\left(2-\frac{x}{a}\right)dx$ (VI)

Write the equation to calculate the total area of shaded region in P5.44.

$A={\displaystyle \underset{0}{\overset{a}{\int }}d{A}_1+}{\displaystyle \underset{a}{\overset{2a}{\int }}d{A}_2}$

Here, $A$ is the area shaded region in P5.44.

Rewrite the above equation by substituting equation (III) and (VI).

$\begin{array}{c}A={\displaystyle \underset{0}{\overset{a}{\int }}\frac{2b}{a^2}}{x}^{2}dx+{\displaystyle \underset{0}{\overset{2a}{\int }}b\left(2-\frac{x}{a}\right)dx}\\ =\frac{2b}{a^2}{\left[\frac{x^3}{3}\right]}_0^a+b{\left[-\frac{a}{2}{\left(2-\frac{x}{a}\right)}^2\right]}_0^{2a}\\ =\frac{7}{6}ab\end{array}$

Write the expression for ${\displaystyle \int {\overline{x}}_{EL}dA}$.

$\begin{array}{c}{\displaystyle \int {\overline{x}}_{EL}dA}={\displaystyle \underset{0}{\overset{a}{\int }}{\overline{x}}_{EL1}d{A}_1+}{\displaystyle \underset{a}{\overset{2a}{\int }}{\overline{x}}_{EL2}d{A}_2}\\ ={\displaystyle \underset{0}{\overset{A}{\int }}xd{A}_1+}{\displaystyle \underset{a}{\overset{2a}{\int }}xd{A}_2}\end{array}$

Rewrite the above equation by substituting equation (III) and (VI).

$\begin{array}{c}{\displaystyle \int {\overline{x}}_{EL}dA}={\displaystyle \underset{0}{\overset{a}{\int }}x\frac{2b}{a^2}}{x}^{2}dx+{\displaystyle \underset{0}{\overset{2a}{\int }}xb\left(2-\frac{x}{a}\right)dx}\\ =\frac{2b}{a^2}{\left[\frac{x^4}{4}\right]}_0^a+b{\left[x^2-{\left(\frac{x^3}{3a}\right)}^2\right]}_a^{2a}\\ =\frac{1}{6}{a}^{2}b+b\left[\left({\left(2a\right)}^2-a^2\right)+\frac{1}{3a}\left({\left(2a\right)}^2-a^3\right)\right]\\ =\frac{7}{6}{a}^{2}b\end{array}$

Write the expression for ${\displaystyle \int {\overline{y}}_{EL}dA}$.

${\displaystyle \int {\overline{y}}_{EL}dA}={\displaystyle \underset{0}{\overset{a}{\int }}{\overline{y}}_{EL1}d{A}_1+}{\displaystyle \underset{a}{\overset{2a}{\int }}{\overline{y}}_{EL2}d{A}_2}$

Rewrite the above equation by substituting equations (II), (III), (V) and (VI).

$\begin{array}{c}{\displaystyle \int {\overline{y}}_{EL}dA}={\displaystyle \underset{0}{\overset{a}{\int }}\frac{b}{a^2}{x}^2\frac{2b}{a^2}{x}^{2}dx+}{\displaystyle \underset{a}{\overset{2a}{\int }}\frac{b}{2}\left(2-\frac{x}{a}\right)b\left(2-\frac{x}{a}\right)dx}\\ =\frac{2b^2}{a^4}{\left[\frac{x^5}{5}\right]}_0^a+\frac{b^2}{2}{\left[-\frac{a}{3}{\left(2-\frac{x}{a}\right)}^3\right]}_a^{2a}\\ =\frac{17}{30}a{b}^2\end{array}$

Write the expression for first moment of whole area about y-axis.

$\overline{x}A={\displaystyle \int {\overline{x}}_{EL}dA}$

Here, $\overline{x}$ is the x-coordinate of center of mass of total area.

Rewrite the above relation by substituting $\frac{7}{6}ab$ for $A$ and $\frac{7}{6}{a}^{2}b$ for ${\displaystyle \int {\overline{x}}_{EL}dA}$.

$\overline{x}\left(\frac{7}{6}ab\right)=\frac{7}{6}{a}^{2}b$

Rewrite the above relation in terms of $\overline{x}$.

$\begin{array}{c}\overline{x}=\frac{\frac{7}{6}{a}^{2}b}{\frac{7}{6}ab}\\ =a\end{array}$

Write the expression for first moment of whole area about x-axis.

$\overline{y}A={\displaystyle \int {\overline{y}}_{EL}dA}$

Here, $\overline{y}$ is the y-coordinate of center of mass of total area.

Rewrite the above relation in terms of $\overline{y}$ by substituting $\frac{7}{6}ab$ for $A$ and $\frac{17}{30}a{b}^2$ for ${\displaystyle \int {\overline{y}}_{EL}dA}$.

$\begin{array}{c}\overline{y}=\frac{\frac{17}{30}a{b}^2}{\frac{7}{6}ab}\\ =\frac{17}{35}b\end{array}$

Therefore, the centroid is located at $\left(a,\frac{17}{35}b\right)$.