EP PRECALCULUS-MYLABMATH+ETEXT ACCESS
6th Edition
ISBN: 9780135963173
Author: Blitzer
Publisher: PEARSON CO
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 5.1, Problem 61PE
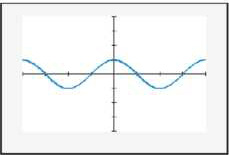
In Exercises 61-66, half of an identity and the graph of this half are given. Use the graph to make a conjecture as to what the right side of the identity should be. Then prove your conjecture.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Please refer below
For the following function f and real number a,
a. find the slope of the tangent line mtan
=
f' (a), and
b. find the equation of the tangent line to f at x = a.
f(x)=
2
=
a = 2
x2
a. Slope:
b. Equation of tangent line: y
Please refer below
Chapter 5 Solutions
EP PRECALCULUS-MYLABMATH+ETEXT ACCESS
Ch. 5.1 - Check Point 1 Verify the identify: .
Ch. 5.1 - Check Point 2 Verify the identity:...Ch. 5.1 - Prob. 3CPCh. 5.1 - Check Point 4 Verify the identity:...Ch. 5.1 - Check Point 5 Verify the identify:...Ch. 5.1 - Prob. 6CPCh. 5.1 - Prob. 7CPCh. 5.1 - Check Point 8 Verify the identity:...Ch. 5.1 - Prob. 1CVCCh. 5.1 - Fill in each blank so that the resulting statement...
Ch. 5.1 - Fill in each blank so that the resulting statement...Ch. 5.1 - Prob. 4CVCCh. 5.1 - Prob. 5CVCCh. 5.1 - In Exercises 1-60, verify each identity.
1.
Ch. 5.1 - In Exercises 1-60, verify each identity.
2.
Ch. 5.1 - Prob. 3PECh. 5.1 - In Exercises 1-60, verify each identity....Ch. 5.1 - Prob. 5PECh. 5.1 - In Exercises 1-60, verify each identity.
6.
Ch. 5.1 - Prob. 7PECh. 5.1 - In Exercises 1-60, verify each identity....Ch. 5.1 - In Exercises 1-60, verify each identity....Ch. 5.1 - Prob. 10PECh. 5.1 - Prob. 11PECh. 5.1 - In Exercises 1-60, verify each identity.
12.
Ch. 5.1 - In Exercises 1-60, verify each identity.
13.
Ch. 5.1 - In Exercises 1-60, verify each identity....Ch. 5.1 - In Exercises 1-60, verify each identity....Ch. 5.1 - In Exercises 1-60, verify each identity.
16.
Ch. 5.1 - In Exercises 1-60, verify each identity.
17.
Ch. 5.1 - Prob. 18PECh. 5.1 - In Exercises 1-60, verify each identity.
19.
Ch. 5.1 - In Exercises 1-60, verify each identity....Ch. 5.1 - Prob. 21PECh. 5.1 - Prob. 22PECh. 5.1 - Prob. 23PECh. 5.1 - In Exercises 1-60, verify each identity.
24.
Ch. 5.1 - Prob. 25PECh. 5.1 - Prob. 26PECh. 5.1 - In Exercises 1-60, verify each identity....Ch. 5.1 - In Exercises 1-60, verify each identity....Ch. 5.1 - Prob. 29PECh. 5.1 - Prob. 30PECh. 5.1 - Prob. 31PECh. 5.1 - In Exercises 1-60, verify each identity.
32.
Ch. 5.1 - In Exercises 1-60, verify each identity.
33.
Ch. 5.1 - In Exercises 1-60, verify each identity....Ch. 5.1 - Prob. 35PECh. 5.1 - In Exercises 1-60, verify each identity....Ch. 5.1 - In Exercises 1-60, verify each identity....Ch. 5.1 - Prob. 38PECh. 5.1 - Prob. 39PECh. 5.1 - In Exercises 1-60, verify each identity....Ch. 5.1 - Prob. 41PECh. 5.1 - Prob. 42PECh. 5.1 - Prob. 43PECh. 5.1 - Prob. 44PECh. 5.1 - Prob. 45PECh. 5.1 - In Exercises 1-60, verify each identity.
46.
Ch. 5.1 - In Exercises 1-60, verify each identity.
47.
Ch. 5.1 - Prob. 48PECh. 5.1 - Prob. 49PECh. 5.1 - In Exercises 1-60, verify each identity....Ch. 5.1 - Prob. 51PECh. 5.1 - Prob. 52PECh. 5.1 - Prob. 53PECh. 5.1 - Prob. 54PECh. 5.1 - In Exercises 1-60, verify each identity.
55.
Ch. 5.1 - Prob. 56PECh. 5.1 - Prob. 57PECh. 5.1 - Prob. 58PECh. 5.1 - In Exercises 1-60, verify each identity.
59.
Ch. 5.1 - In Exercises 1-60, verify each identity....Ch. 5.1 - In Exercises 61-66, half of an identity and the...Ch. 5.1 - Prob. 62PECh. 5.1 - Prob. 63PECh. 5.1 - Prob. 64PECh. 5.1 - Prob. 65PECh. 5.1 - In Exercises 61-66, half of an identity and the...Ch. 5.1 - Prob. 67PECh. 5.1 - Prob. 68PECh. 5.1 - Prob. 69PECh. 5.1 - Prob. 70PECh. 5.1 - Prob. 71PECh. 5.1 - Prob. 72PECh. 5.1 - Prob. 73PECh. 5.1 - Prob. 74PECh. 5.1 - Prob. 75PECh. 5.1 - Prob. 76PECh. 5.1 - Prob. 77PECh. 5.1 - Prob. 78PECh. 5.1 - Prob. 79PECh. 5.1 - Prob. 80PECh. 5.1 - Prob. 81PECh. 5.1 - Prob. 82PECh. 5.1 - Prob. 83PECh. 5.1 - Prob. 84PECh. 5.1 - In Exercises 79-87, graph each side of the...Ch. 5.1 - Prob. 86PECh. 5.1 - Prob. 87PECh. 5.1 - Prob. 88PECh. 5.1 - Prob. 89PECh. 5.1 - Prob. 90PECh. 5.1 - Prob. 91PECh. 5.1 - Prob. 92PECh. 5.1 - In Exercises 92-95, verify each identity.
93.
Ch. 5.1 - In Exercises 92-95, verify each identity....Ch. 5.1 - Prob. 95PECh. 5.1 - Prob. 96PECh. 5.1 - Prob. 97PECh. 5.1 - Prob. 98PECh. 5.1 - 99. Determine the amplitude and period of .
Then...Ch. 5.1 - Find the inverse of f(x)=x1x+1. (Section 2.7,...Ch. 5.1 - Prob. 101PECh. 5.1 - Prob. 102PECh. 5.1 - Exercises 101-103 will help you prepare for the...Ch. 5.2 - Check Point 1 We know that cos30=32. Obtain this...Ch. 5.2 - Prob. 2CPCh. 5.2 - Prob. 3CPCh. 5.2 - Prob. 4CPCh. 5.2 - Prob. 5CPCh. 5.2 - Check Point 6 Figure 5.5 shows the graph of...Ch. 5.2 - Prob. 7CPCh. 5.2 - Prob. 1CVCCh. 5.2 - Prob. 2CVCCh. 5.2 - Prob. 3CVCCh. 5.2 - Prob. 4CVCCh. 5.2 - Prob. 5CVCCh. 5.2 - Prob. 6CVCCh. 5.2 - Prob. 7CVCCh. 5.2 - Prob. 8CVCCh. 5.2 - Use the formula for the cosine of the difference...Ch. 5.2 - Prob. 2PECh. 5.2 - Use the formula for the cosine of the difference...Ch. 5.2 - Prob. 4PECh. 5.2 - Prob. 5PECh. 5.2 - Prob. 6PECh. 5.2 - Prob. 7PECh. 5.2 - Prob. 8PECh. 5.2 - Prob. 9PECh. 5.2 - Prob. 10PECh. 5.2 - Prob. 11PECh. 5.2 - Prob. 12PECh. 5.2 - Use one or more of the six sum and difference...Ch. 5.2 - Prob. 14PECh. 5.2 - Prob. 15PECh. 5.2 - Use one or more of the six sum and difference...Ch. 5.2 - Prob. 17PECh. 5.2 - Prob. 18PECh. 5.2 - Prob. 19PECh. 5.2 - Prob. 20PECh. 5.2 - Use one or more of the six sum and difference...Ch. 5.2 - Prob. 22PECh. 5.2 - Prob. 23PECh. 5.2 - Prob. 24PECh. 5.2 - Prob. 25PECh. 5.2 - Prob. 26PECh. 5.2 - Prob. 27PECh. 5.2 - Prob. 28PECh. 5.2 - Prob. 29PECh. 5.2 - Prob. 30PECh. 5.2 - Prob. 31PECh. 5.2 - Prob. 32PECh. 5.2 - Use one or more of the six sum and difference...Ch. 5.2 - Prob. 34PECh. 5.2 - Prob. 35PECh. 5.2 - Prob. 36PECh. 5.2 - Prob. 37PECh. 5.2 - Prob. 38PECh. 5.2 - Prob. 39PECh. 5.2 - Prob. 40PECh. 5.2 - Prob. 41PECh. 5.2 - Prob. 42PECh. 5.2 - Prob. 43PECh. 5.2 - Prob. 44PECh. 5.2 - Prob. 45PECh. 5.2 - Prob. 46PECh. 5.2 - Prob. 47PECh. 5.2 - Prob. 48PECh. 5.2 - Prob. 49PECh. 5.2 - Prob. 50PECh. 5.2 - Prob. 51PECh. 5.2 - Prob. 52PECh. 5.2 - Prob. 53PECh. 5.2 - Prob. 54PECh. 5.2 - Prob. 55PECh. 5.2 - Prob. 56PECh. 5.2 - Prob. 57PECh. 5.2 - Prob. 58PECh. 5.2 - Prob. 59PECh. 5.2 - Prob. 60PECh. 5.2 - Prob. 61PECh. 5.2 - Prob. 62PECh. 5.2 - Prob. 63PECh. 5.2 - In Exercises 57-64, find the exact value of the...Ch. 5.2 - Prob. 65PECh. 5.2 - Prob. 66PECh. 5.2 - In Exercises 65-68, the graph with the given...Ch. 5.2 - Prob. 68PECh. 5.2 - Prob. 69PECh. 5.2 - Prob. 70PECh. 5.2 - Prob. 71PECh. 5.2 - Prob. 72PECh. 5.2 - Prob. 73PECh. 5.2 - Prob. 74PECh. 5.2 - Prob. 75PECh. 5.2 - Prob. 76PECh. 5.2 - Prob. 77PECh. 5.2 - Prob. 78PECh. 5.2 - A ball attached to a spring is raised 2 feet and...Ch. 5.2 - Prob. 80PECh. 5.2 - Prob. 81PECh. 5.2 - Prob. 82PECh. 5.2 - Prob. 83PECh. 5.2 - Prob. 84PECh. 5.2 - Prob. 85PECh. 5.2 - Prob. 86PECh. 5.2 - Prob. 87PECh. 5.2 - Prob. 88PECh. 5.2 - Prob. 89PECh. 5.2 - Prob. 90PECh. 5.2 - Prob. 91PECh. 5.2 - Prob. 92PECh. 5.2 - Prob. 93PECh. 5.2 - Prob. 94PECh. 5.2 - Prob. 95PECh. 5.2 - Prob. 96PECh. 5.2 - Prob. 97PECh. 5.2 - Prob. 98PECh. 5.2 - Prob. 99PECh. 5.2 - Prob. 100PECh. 5.2 - Prob. 101PECh. 5.2 - Prob. 102PECh. 5.2 - Prob. 103PECh. 5.2 - Prob. 104PECh. 5.2 - Prob. 105PECh. 5.2 - Prob. 106PECh. 5.2 - 107. A hot-air balloon is rising vertically. From...Ch. 5.2 - Use a sketch to find the exact value of...Ch. 5.2 - Prob. 109PECh. 5.2 - Prob. 110PECh. 5.2 - Prob. 111PECh. 5.2 - Prob. 112PECh. 5.3 - Check Point 1 if and lies in quadrant II, find...Ch. 5.3 - Check Point 2 Find the exact value of...Ch. 5.3 - Check Point 3 Verify the identity:
Ch. 5.3 - Prob. 4CPCh. 5.3 - Check Point 5 Use cos to find the exact value of...Ch. 5.3 - Prob. 6CPCh. 5.3 - Check Point 7 Verify the identify : .
Ch. 5.3 - Prob. 1CVCCh. 5.3 - Prob. 2CVCCh. 5.3 - Prob. 3CVCCh. 5.3 - Prob. 4CVCCh. 5.3 - Prob. 5CVCCh. 5.3 - Prob. 6CVCCh. 5.3 - Prob. 7CVCCh. 5.3 - Prob. 8CVCCh. 5.3 - Prob. 9CVCCh. 5.3 - Prob. 10CVCCh. 5.3 - Prob. 11CVCCh. 5.3 - Prob. 12CVCCh. 5.3 - Prob. 13CVCCh. 5.3 - Prob. 14CVCCh. 5.3 - Prob. 15CVCCh. 5.3 - In Exercises 1-6, use the figures to find the...Ch. 5.3 - Prob. 2PECh. 5.3 - In Exercises 1-6, use the figures to find the...Ch. 5.3 - Prob. 4PECh. 5.3 - Prob. 5PECh. 5.3 - Prob. 6PECh. 5.3 - In Exercises 7-14, use the given information to...Ch. 5.3 - Prob. 8PECh. 5.3 - Prob. 9PECh. 5.3 - In Exercises 7-14, use the given information to...Ch. 5.3 - Prob. 11PECh. 5.3 - Prob. 12PECh. 5.3 - Prob. 13PECh. 5.3 - Prob. 14PECh. 5.3 - Prob. 15PECh. 5.3 - Prob. 16PECh. 5.3 - Prob. 17PECh. 5.3 - Prob. 18PECh. 5.3 - In Exercises 15-22, write each expression as the...Ch. 5.3 - In Exercises 15-22, write each expression as the...Ch. 5.3 - In Exercises 15-22, write each expression as the...Ch. 5.3 - Prob. 22PECh. 5.3 - Prob. 23PECh. 5.3 - Prob. 24PECh. 5.3 - Prob. 25PECh. 5.3 - Prob. 26PECh. 5.3 - Prob. 27PECh. 5.3 - Prob. 28PECh. 5.3 - Prob. 29PECh. 5.3 - Prob. 30PECh. 5.3 - Prob. 31PECh. 5.3 - Prob. 32PECh. 5.3 - Prob. 33PECh. 5.3 - Prob. 34PECh. 5.3 - Prob. 35PECh. 5.3 - Prob. 36PECh. 5.3 - Prob. 37PECh. 5.3 - Prob. 38PECh. 5.3 - Prob. 39PECh. 5.3 - Prob. 40PECh. 5.3 - Prob. 41PECh. 5.3 - Prob. 42PECh. 5.3 - Prob. 43PECh. 5.3 - Prob. 44PECh. 5.3 - Prob. 45PECh. 5.3 - Prob. 46PECh. 5.3 - In Exercises 47-54, use the figures to find the...Ch. 5.3 - Prob. 48PECh. 5.3 - Prob. 49PECh. 5.3 - Prob. 50PECh. 5.3 - Prob. 51PECh. 5.3 - Prob. 52PECh. 5.3 - In Exercises 47-54, use the figures to find the...Ch. 5.3 - Prob. 54PECh. 5.3 - In Exercises 55-58, use the given information to...Ch. 5.3 - Prob. 56PECh. 5.3 - In Exercises 55-58, use the given information to...Ch. 5.3 - Prob. 58PECh. 5.3 - Prob. 59PECh. 5.3 - Prob. 60PECh. 5.3 - Prob. 61PECh. 5.3 - Prob. 62PECh. 5.3 - In Exercises 59-68, verify each identity.
63.
Ch. 5.3 - Prob. 64PECh. 5.3 - Prob. 65PECh. 5.3 - Prob. 66PECh. 5.3 - Prob. 67PECh. 5.3 - Prob. 68PECh. 5.3 - Prob. 69PECh. 5.3 - In Exercises 69-78, half of an identity and the...Ch. 5.3 - Prob. 71PECh. 5.3 - Prob. 72PECh. 5.3 - Prob. 73PECh. 5.3 - Prob. 74PECh. 5.3 - Prob. 75PECh. 5.3 - Prob. 76PECh. 5.3 - Prob. 77PECh. 5.3 - Prob. 78PECh. 5.3 - Prob. 79PECh. 5.3 - Prob. 80PECh. 5.3 - Prob. 81PECh. 5.3 - Prob. 82PECh. 5.3 - Prob. 83PECh. 5.3 - Prob. 84PECh. 5.3 - Prob. 85PECh. 5.3 - Prob. 86PECh. 5.3 - Prob. 87PECh. 5.3 - Prob. 88PECh. 5.3 - Prob. 89PECh. 5.3 - Prob. 90PECh. 5.3 - Prob. 91PECh. 5.3 - Prob. 92PECh. 5.3 - Prob. 93PECh. 5.3 - Prob. 94PECh. 5.3 - Prob. 95PECh. 5.3 - Prob. 96PECh. 5.3 - Prob. 97PECh. 5.3 - Prob. 98PECh. 5.3 - In Exercises 99-101, graph each equation in a...Ch. 5.3 - Prob. 100PECh. 5.3 - Prob. 101PECh. 5.3 - Prob. 102PECh. 5.3 - Make Sense? In Exercises 102-105, determine...Ch. 5.3 - Prob. 104PECh. 5.3 - Prob. 105PECh. 5.3 - Prob. 106PECh. 5.3 - Prob. 107PECh. 5.3 - Prob. 108PECh. 5.3 - In Exercises 107-110, find the exact value of each...Ch. 5.3 - Prob. 110PECh. 5.3 - 111. Use a right triangle to write as an...Ch. 5.3 - Prob. 112PECh. 5.3 - Prob. 113PECh. 5.3 - Prob. 114PECh. 5.3 - Prob. 115PECh. 5.3 - Prob. 116PECh. 5.3 - Prob. 117PECh. 5.3 - Prob. 118PECh. 5.3 - Prob. 1MCCPCh. 5.3 - Prob. 2MCCPCh. 5.3 - Prob. 3MCCPCh. 5.3 - Prob. 4MCCPCh. 5.3 - Prob. 5MCCPCh. 5.3 - Prob. 6MCCPCh. 5.3 - Prob. 7MCCPCh. 5.3 - Prob. 8MCCPCh. 5.3 - In Exercises 1-18, verify each identity....Ch. 5.3 - Prob. 10MCCPCh. 5.3 - Prob. 11MCCPCh. 5.3 - Prob. 12MCCPCh. 5.3 - Prob. 13MCCPCh. 5.3 - Prob. 14MCCPCh. 5.3 - Prob. 15MCCPCh. 5.3 - Prob. 16MCCPCh. 5.3 - Prob. 17MCCPCh. 5.3 - Prob. 18MCCPCh. 5.3 - Prob. 19MCCPCh. 5.3 - Prob. 20MCCPCh. 5.3 - Prob. 21MCCPCh. 5.3 - Prob. 22MCCPCh. 5.3 - Prob. 23MCCPCh. 5.3 - Prob. 24MCCPCh. 5.3 - Prob. 25MCCPCh. 5.3 - Prob. 26MCCPCh. 5.4 - Check Point 1 Express each of the following...Ch. 5.4 - Prob. 2CPCh. 5.4 - Prob. 3CPCh. 5.4 - Prob. 1CVCCh. 5.4 - Prob. 2CVCCh. 5.4 - Prob. 3CVCCh. 5.4 - Prob. 4CVCCh. 5.4 - Prob. 5CVCCh. 5.4 - Prob. 6CVCCh. 5.4 - Prob. 7CVCCh. 5.4 - Prob. 8CVCCh. 5.4 - Be sure that you’ve familiarized yourself with the...Ch. 5.4 - Prob. 2PECh. 5.4 - Prob. 3PECh. 5.4 - Prob. 4PECh. 5.4 - Prob. 5PECh. 5.4 - Prob. 6PECh. 5.4 - Prob. 7PECh. 5.4 - Prob. 8PECh. 5.4 - Prob. 9PECh. 5.4 - Prob. 10PECh. 5.4 - Prob. 11PECh. 5.4 - Prob. 12PECh. 5.4 - Prob. 13PECh. 5.4 - Prob. 14PECh. 5.4 - Prob. 15PECh. 5.4 - Prob. 16PECh. 5.4 - Prob. 17PECh. 5.4 - Prob. 18PECh. 5.4 - Prob. 19PECh. 5.4 - Prob. 20PECh. 5.4 - Prob. 21PECh. 5.4 - Prob. 22PECh. 5.4 - Prob. 23PECh. 5.4 - Prob. 24PECh. 5.4 - Prob. 25PECh. 5.4 - Prob. 26PECh. 5.4 - Prob. 27PECh. 5.4 - Prob. 28PECh. 5.4 - Prob. 29PECh. 5.4 - Prob. 30PECh. 5.4 - Prob. 31PECh. 5.4 - Prob. 32PECh. 5.4 - Prob. 33PECh. 5.4 - Prob. 34PECh. 5.4 - Prob. 35PECh. 5.4 - Prob. 36PECh. 5.4 - Prob. 37PECh. 5.4 - Prob. 38PECh. 5.4 - Prob. 39PECh. 5.4 - In Exercises 39-42, use words to describe the...Ch. 5.4 - Prob. 41PECh. 5.4 - Prob. 42PECh. 5.4 - Describe identities that can be verified using the...Ch. 5.4 - Prob. 44PECh. 5.4 - Prob. 45PECh. 5.4 - Prob. 46PECh. 5.4 - Prob. 47PECh. 5.4 - Prob. 48PECh. 5.4 - Prob. 49PECh. 5.4 - Prob. 50PECh. 5.4 - Prob. 51PECh. 5.4 - Prob. 52PECh. 5.4 - Prob. 53PECh. 5.4 - Make Sense? In Exercises 52-55, determine whether...Ch. 5.4 - Prob. 55PECh. 5.4 - Prob. 56PECh. 5.4 - Prob. 57PECh. 5.4 - Prob. 58PECh. 5.4 - Prob. 59PECh. 5.4 - Prob. 60PECh. 5.4 - Prob. 61PECh. 5.4 - Prob. 62PECh. 5.4 - 63. A circle has a radius of 8 inches. Find the...Ch. 5.4 - Prob. 64PECh. 5.4 - Prob. 65PECh. 5.4 - Prob. 66PECh. 5.4 - Prob. 67PECh. 5.4 - Prob. 68PECh. 5.5 - Check Point 1 Solve the equation: 5sinx=3sinx+3Ch. 5.5 - Prob. 2CPCh. 5.5 - Prob. 3CPCh. 5.5 - Prob. 4CPCh. 5.5 - Prob. 5CPCh. 5.5 - Check Point 6 Solve the equation: .
Ch. 5.5 - Prob. 7CPCh. 5.5 - Prob. 8CPCh. 5.5 - Prob. 9CPCh. 5.5 - Prob. 10CPCh. 5.5 - Check Point 11 Solve each equation, correct to...Ch. 5.5 - Prob. 12CPCh. 5.5 - Prob. 1CVCCh. 5.5 - Prob. 2CVCCh. 5.5 - Prob. 3CVCCh. 5.5 - Prob. 4CVCCh. 5.5 - Prob. 5CVCCh. 5.5 - Prob. 6CVCCh. 5.5 - Prob. 7CVCCh. 5.5 - Prob. 8CVCCh. 5.5 - In Exercises 1-10, use substitution to determine...Ch. 5.5 - Prob. 1PECh. 5.5 - In Exercises 1-10, use substitution to determine...Ch. 5.5 - Prob. 3PECh. 5.5 - Prob. 4PECh. 5.5 - Prob. 5PECh. 5.5 - Prob. 6PECh. 5.5 - Prob. 7PECh. 5.5 - Prob. 8PECh. 5.5 - Prob. 9PECh. 5.5 - Prob. 10PECh. 5.5 - In Exercises 11-24, find all solutions of each...Ch. 5.5 - Prob. 12PECh. 5.5 - Prob. 13PECh. 5.5 - Prob. 14PECh. 5.5 - Prob. 15PECh. 5.5 - Prob. 16PECh. 5.5 - Prob. 17PECh. 5.5 - Prob. 18PECh. 5.5 - Prob. 19PECh. 5.5 - Prob. 20PECh. 5.5 - In Exercises 11-24, find all solutions of each...Ch. 5.5 - Prob. 22PECh. 5.5 - Prob. 23PECh. 5.5 - Prob. 24PECh. 5.5 - Prob. 25PECh. 5.5 - Prob. 26PECh. 5.5 - Prob. 27PECh. 5.5 - Prob. 28PECh. 5.5 - Prob. 29PECh. 5.5 - Prob. 30PECh. 5.5 - Prob. 31PECh. 5.5 - Prob. 32PECh. 5.5 - Prob. 33PECh. 5.5 - Prob. 34PECh. 5.5 - Prob. 35PECh. 5.5 - Prob. 36PECh. 5.5 - Exercises 25-38 involve equations with multiple...Ch. 5.5 - Prob. 38PECh. 5.5 - Prob. 39PECh. 5.5 - Prob. 40PECh. 5.5 - Prob. 41PECh. 5.5 - Prob. 42PECh. 5.5 - Prob. 43PECh. 5.5 - Prob. 44PECh. 5.5 - Prob. 45PECh. 5.5 - Prob. 46PECh. 5.5 - Prob. 47PECh. 5.5 - Prob. 48PECh. 5.5 - Prob. 49PECh. 5.5 - Prob. 50PECh. 5.5 - Prob. 51PECh. 5.5 - Prob. 52PECh. 5.5 - Prob. 53PECh. 5.5 - Prob. 54PECh. 5.5 - Prob. 55PECh. 5.5 - Prob. 56PECh. 5.5 - Prob. 57PECh. 5.5 - Prob. 58PECh. 5.5 - Prob. 59PECh. 5.5 - Prob. 60PECh. 5.5 - Prob. 61PECh. 5.5 - Prob. 62PECh. 5.5 - Prob. 63PECh. 5.5 - In Exercises 63-84, use an identity to solve each...Ch. 5.5 - Prob. 65PECh. 5.5 - In Exercises 63-84, use an identity to solve each...Ch. 5.5 - Prob. 67PECh. 5.5 - Prob. 68PECh. 5.5 - Prob. 69PECh. 5.5 - Prob. 70PECh. 5.5 - Prob. 71PECh. 5.5 - Prob. 72PECh. 5.5 - In Exercises 63-84, use an identity to solve each...Ch. 5.5 - Prob. 74PECh. 5.5 - Prob. 75PECh. 5.5 - Prob. 76PECh. 5.5 - Prob. 77PECh. 5.5 - Prob. 78PECh. 5.5 - Prob. 79PECh. 5.5 - Prob. 80PECh. 5.5 - Prob. 81PECh. 5.5 - In Exercises 63-84, use an identity to solve each...Ch. 5.5 - Prob. 83PECh. 5.5 - In Exercises 63-84, use an identity to solve each...Ch. 5.5 - Prob. 85PECh. 5.5 - Prob. 86PECh. 5.5 - Prob. 87PECh. 5.5 - Prob. 88PECh. 5.5 - Prob. 89PECh. 5.5 - Prob. 90PECh. 5.5 - Prob. 91PECh. 5.5 - Prob. 92PECh. 5.5 - Prob. 93PECh. 5.5 - Prob. 94PECh. 5.5 - Prob. 95PECh. 5.5 - Prob. 96PECh. 5.5 - Prob. 97PECh. 5.5 - Prob. 98PECh. 5.5 - Prob. 99PECh. 5.5 - Prob. 100PECh. 5.5 - Prob. 101PECh. 5.5 - Prob. 102PECh. 5.5 - Prob. 103PECh. 5.5 - Prob. 104PECh. 5.5 - Prob. 105PECh. 5.5 - Prob. 106PECh. 5.5 - Prob. 107PECh. 5.5 - Prob. 108PECh. 5.5 - Prob. 109PECh. 5.5 - Prob. 110PECh. 5.5 - Prob. 111PECh. 5.5 - Prob. 112PECh. 5.5 - Prob. 113PECh. 5.5 - In Exercises 97-116, use the most appropriate...Ch. 5.5 - Prob. 115PECh. 5.5 - Prob. 116PECh. 5.5 - Prob. 117PECh. 5.5 - Prob. 118PECh. 5.5 - Prob. 119PECh. 5.5 - Prob. 120PECh. 5.5 - Prob. 121PECh. 5.5 - Prob. 122PECh. 5.5 - Prob. 123PECh. 5.5 - Prob. 124PECh. 5.5 - Prob. 125PECh. 5.5 - Prob. 126PECh. 5.5 - Prob. 127PECh. 5.5 - Prob. 128PECh. 5.5 - Prob. 129PECh. 5.5 - Prob. 130PECh. 5.5 - Prob. 131PECh. 5.5 - Prob. 132PECh. 5.5 - Prob. 133PECh. 5.5 - Prob. 134PECh. 5.5 - Prob. 135PECh. 5.5 - Prob. 136PECh. 5.5 - Prob. 137PECh. 5.5 - Prob. 138PECh. 5.5 - Prob. 139PECh. 5.5 - Prob. 140PECh. 5.5 - Prob. 141PECh. 5.5 - Prob. 142PECh. 5.5 - Prob. 143PECh. 5.5 - Prob. 144PECh. 5.5 - Prob. 145PECh. 5.5 - Prob. 146PECh. 5.5 - Prob. 147PECh. 5.5 - Prob. 148PECh. 5.5 - Prob. 149PECh. 5.5 - Prob. 150PECh. 5.5 - Prob. 151PECh. 5.5 - Make Sense? In Exercises 152-155, determine...Ch. 5.5 - Prob. 153PECh. 5.5 - Prob. 154PECh. 5.5 - Prob. 155PECh. 5.5 - Prob. 156PECh. 5.5 - Prob. 157PECh. 5.5 - Prob. 158PECh. 5.5 - Prob. 159PECh. 5.5 - Prob. 160PECh. 5.5 - Prob. 161PECh. 5.5 - Prob. 162PECh. 5.5 - Prob. 163PECh. 5.5 - Prob. 164PECh. 5.5 - Prob. 165PECh. 5.5 - Prob. 166PECh. 5.5 - Prob. 167PECh. 5.5 - Prob. 168PECh. 5 - In Exercises 1-13, verify each identity....Ch. 5 - In Exercises 1-13, verify each identity.
2.
Ch. 5 - Prob. 3RECh. 5 - In Exercises 1-13, verify each identity....Ch. 5 - Prob. 5RECh. 5 - Prob. 6RECh. 5 - Prob. 7RECh. 5 - In Exercises 1-13, verify each identity....Ch. 5 - Prob. 9RECh. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Prob. 12RECh. 5 - Prob. 13RECh. 5 - Prob. 14RECh. 5 - Prob. 15RECh. 5 - Prob. 16RECh. 5 - Prob. 17RECh. 5 - Prob. 18RECh. 5 - Prob. 19RECh. 5 - Prob. 20RECh. 5 - Prob. 21RECh. 5 - Prob. 22RECh. 5 - Prob. 23RECh. 5 - Prob. 24RECh. 5 - Prob. 25RECh. 5 - Prob. 26RECh. 5 - Prob. 27RECh. 5 - Prob. 28RECh. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - Prob. 33RECh. 5 - Prob. 34RECh. 5 - Prob. 35RECh. 5 - Prob. 36RECh. 5 - Prob. 37RECh. 5 - Prob. 38RECh. 5 - Prob. 39RECh. 5 - Prob. 40RECh. 5 - Prob. 41RECh. 5 - Prob. 42RECh. 5 - Prob. 43RECh. 5 - Prob. 44RECh. 5 - Prob. 45RECh. 5 - Prob. 46RECh. 5 - Prob. 47RECh. 5 - Prob. 48RECh. 5 - Prob. 49RECh. 5 - Prob. 50RECh. 5 - Prob. 51RECh. 5 - Prob. 52RECh. 5 - Prob. 53RECh. 5 - Prob. 54RECh. 5 - Prob. 55RECh. 5 - Prob. 56RECh. 5 - Prob. 57RECh. 5 - Prob. 58RECh. 5 - Prob. 59RECh. 5 - Prob. 60RECh. 5 - Prob. 61RECh. 5 - Prob. 62RECh. 5 - Prob. 63RECh. 5 - Prob. 64RECh. 5 - Prob. 65RECh. 5 - Prob. 66RECh. 5 - Prob. 67RECh. 5 - Prob. 68RECh. 5 - Prob. 69RECh. 5 - Prob. 1TCh. 5 - Prob. 2TCh. 5 - Prob. 3TCh. 5 - Prob. 4TCh. 5 - Prob. 5TCh. 5 - Prob. 6TCh. 5 - Prob. 7TCh. 5 - Prob. 8TCh. 5 - Prob. 9TCh. 5 - In Exercises 6-11, verify each identity.
10.
Ch. 5 - Prob. 11TCh. 5 - Prob. 12TCh. 5 - Prob. 13TCh. 5 - Prob. 14TCh. 5 - Prob. 15TCh. 5 - In Exercises 12-18, solve each equation on the...Ch. 5 - Prob. 17TCh. 5 - Prob. 18TCh. 5 - Prob. 1CRECh. 5 - Prob. 2CRECh. 5 - Prob. 3CRECh. 5 - Prob. 4CRECh. 5 - Prob. 5CRECh. 5 - Prob. 6CRECh. 5 - Prob. 7CRECh. 5 - Prob. 8CRECh. 5 - Prob. 9CRECh. 5 - Prob. 10CRECh. 5 - Prob. 11CRECh. 5 - Prob. 12CRECh. 5 - Prob. 13CRECh. 5 - Prob. 14CRECh. 5 - Prob. 15CRECh. 5 - Prob. 16CRECh. 5 - Prob. 17CRECh. 5 - Prob. 18CRECh. 5 - Prob. 19CRECh. 5 - Prob. 20CRE
Additional Math Textbook Solutions
Find more solutions based on key concepts
True or False The quotient of two polynomial expressions is a rational expression, (p. A35)
Precalculus
First Derivative Test a. Locale the critical points of f. b. Use the First Derivative Test to locale the local ...
Calculus: Early Transcendentals (2nd Edition)
Find all solutions of each equation in the interval .
Precalculus: A Unit Circle Approach (3rd Edition)
In Exercises 9-20, use the data in the following table, which lists drive-thru order accuracy at popular fast f...
Elementary Statistics (13th Edition)
1. How is a sample related to a population?
Elementary Statistics: Picturing the World (7th Edition)
Teacher Salaries
The following data from several years ago represent salaries (in dollars) from a school distri...
Elementary Statistics: A Step By Step Approach
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Let f(x, y) = 2x + 3y+ In(xy)arrow_forward(3) (16 points) Let D = [0, π/2] × [0, 7/6]. Define T: DCR2 R3 by → T(0, 4) = (2 sin cos 0, 2 sin sin 0, 2 cos x). Let S be the surface parametrized by T. (a) (8 points) Determine the normal, call it n(p), for the tangent plane TS at an arbitrary point p = T(0, 4). (b) (4 points) Show that n(p) parallel to the position vector T(0, 4) determined by p? Do the two vectors have the same direction or opposite direction? Explain. (c) (4 points) At which points p, if any, is TS parallel to the xy-plane?arrow_forward5:19 0 TEMU TEMU >>> 49 95% University at Albany - Single Sig... L Lumen OHM D2L HW4- AMAT100-Precal HW4 Score: 12.99/21 Answered: 18/21 × Question 16 Score on last try: 0 of 1 pts. See Details for more. > Next question Get a similar question You can retry this question below Find the inverse for the function k(x) = √√7x+12 k-¹(x) = Question Help: Video Message instructor Submit Question esc ||| F1 80 ୮ (x) = tarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Fundamental Trigonometric Identities: Reciprocal, Quotient, and Pythagorean Identities; Author: Mathispower4u;https://www.youtube.com/watch?v=OmJ5fxyXrfg;License: Standard YouTube License, CC-BY