Geometry, Student Edition
1st Edition
ISBN: 9780078884849
Author: McGraw-Hill, McGraw Hill
Publisher: Glencoe/McGraw-Hill School Pub Co
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 5.1, Problem 4BCYP
a.
To determine
ToDraw:An acute
a.
Expert Solution
Explanation of Solution
Given:The relation among three points of concurrency in a triangle.
An acute triangle whose all three
Below is figure of acute triangle.
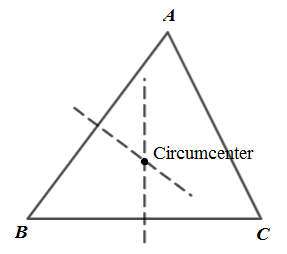
Circumcenter: It is point of intersection of perpendicular bisector of each sides. As shown in below figure.
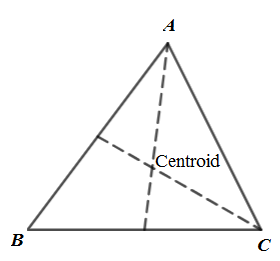
Centroid: It is intersection of medians of triangle. As shown in below figure.
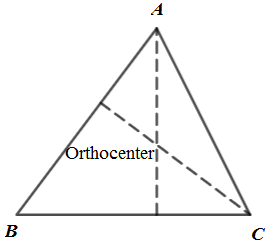
Orthocenter: It is intersetion point of altitudes of a triangle.
b.
To determine
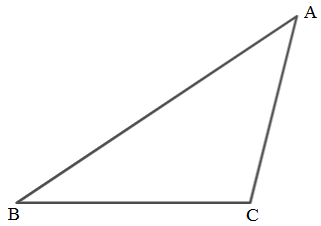
To Draw: An obstude triangle and find the circumcenter, centroid and orthocenter.
b.
Expert Solution
Explanation of Solution
Given:The relation among three points of concurrency in a triangle.
An obtude triangle whose one angle is obtuse. An obtude angle is greater than
Below is figure of obtuse triangle.
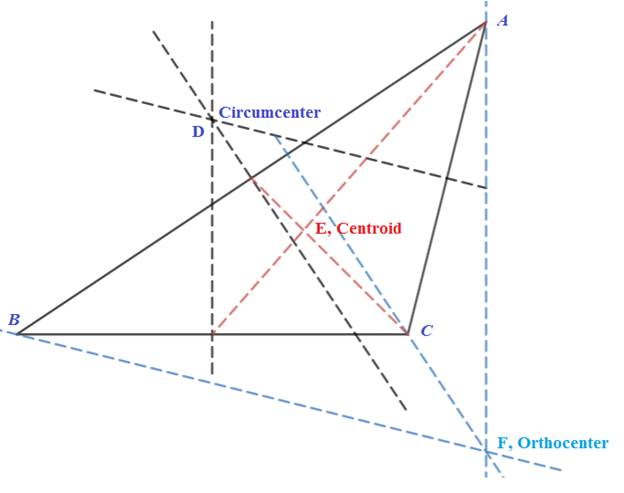
Circumcenter: It is point of intersection of perpendicular bisector of each sides. As shown in below figure.
Centroid: It is intersection of medians of triangle. As shown in below figure.
Orthocenter: It is intersetion point of altitudes of a triangle.
c.
To determine
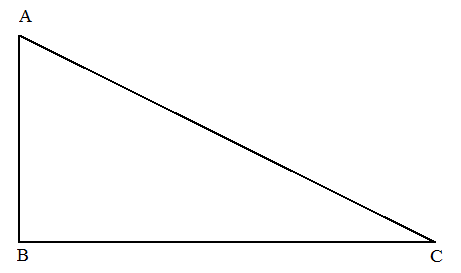
To Draw:Anright triangle and find the circumcenter, centroid and orthocenter.
c.
Expert Solution
Explanation of Solution
Given:The relation among three points of concurrency in a triangle.
An right triangle whose one angle is right.
Below is figure of right triangle.
Circumcenter: It is point of intersection of perpendicular bisector of each sides. As shown in below figure.
Centroid: It is intersection of medians of triangle. As shown in below figure.
Orthocenter: It is intersetion point of altitudes of a triangle.
d.
To determine
To explain:The conjecture of all three centers.
d.
Expert Solution
Explanation of Solution
Given:The relation among three points of concurrency in a triangle.
Circumcenter: It is point of intersection of perpendicular bisector of each sides. As shown in below figure.
Centroid: It is intersection of medians of triangle. As shown in below figure.
Orthocenter: It is intersetion point of altitudes of a triangle.
In acute triangle all three centre lie inside the triangle.
In obtuse triangle orthocenter and circumcenter lie outside the triangle. Centroid lie inside the triangle.
In right triangle circumcenter lie on hypotenuse and orthocenter is opposite vertex of hypotenuse of triangle. Centroid lie inside the triangle.
Chapter 5 Solutions
Geometry, Student Edition
Ch. 5.1 - Prob. 1ACYPCh. 5.1 - Prob. 1BCYPCh. 5.1 - Prob. 1CCYPCh. 5.1 - Prob. 2CYPCh. 5.1 - Prob. 3ACYPCh. 5.1 - Prob. 3BCYPCh. 5.1 - Prob. 3CCYPCh. 5.1 - Prob. 4ACYPCh. 5.1 - Prob. 4BCYPCh. 5.1 - Prob. 1CYU
Ch. 5.1 - Prob. 2CYUCh. 5.1 - Prob. 3CYUCh. 5.1 - Prob. 4CYUCh. 5.1 - Prob. 5CYUCh. 5.1 - Prob. 6CYUCh. 5.1 - Prob. 7CYUCh. 5.1 - Prob. 8CYUCh. 5.1 - Prob. 9PPSCh. 5.1 - Prob. 10PPSCh. 5.1 - Prob. 11PPSCh. 5.1 - Prob. 12PPSCh. 5.1 - Prob. 13PPSCh. 5.1 - Prob. 14PPSCh. 5.1 - Prob. 15PPSCh. 5.1 - Prob. 16PPSCh. 5.1 - Prob. 17PPSCh. 5.1 - Prob. 18PPSCh. 5.1 - Prob. 19PPSCh. 5.1 - Prob. 20PPSCh. 5.1 - Prob. 21PPSCh. 5.1 - Prob. 22PPSCh. 5.1 - Prob. 23PPSCh. 5.1 - Prob. 24PPSCh. 5.1 - Prob. 25PPSCh. 5.1 - Prob. 26PPSCh. 5.1 - Prob. 27PPSCh. 5.1 - Prob. 28PPSCh. 5.1 - Prob. 29PPSCh. 5.1 - Prob. 30PPSCh. 5.1 - Prob. 31PPSCh. 5.1 - Prob. 32PPSCh. 5.1 - Prob. 33PPSCh. 5.1 - Prob. 34PPSCh. 5.1 - Prob. 35PPSCh. 5.1 - Prob. 36PPSCh. 5.1 - Prob. 37PPSCh. 5.1 - Prob. 38PPSCh. 5.1 - Prob. 39PPSCh. 5.1 - Prob. 40PPSCh. 5.1 - Prob. 41PPSCh. 5.1 - Prob. 42PPSCh. 5.1 - Prob. 43PPSCh. 5.1 - Prob. 44PPSCh. 5.1 - Prob. 45PPSCh. 5.1 - Prob. 46PPSCh. 5.1 - Prob. 47PPSCh. 5.1 - Prob. 48HPCh. 5.1 - Prob. 49HPCh. 5.1 - Prob. 50HPCh. 5.1 - Prob. 51HPCh. 5.1 - Prob. 52HPCh. 5.1 - Prob. 53HPCh. 5.1 - Prob. 54HPCh. 5.1 - Prob. 55STPCh. 5.1 - Prob. 56STPCh. 5.1 - Prob. 57STPCh. 5.1 - Prob. 58STPCh. 5.1 - Prob. 59SPRCh. 5.1 - Prob. 60SPRCh. 5.1 - Prob. 61SPRCh. 5.1 - Prob. 62SPRCh. 5.1 - Prob. 63SPRCh. 5.1 - Prob. 64SPRCh. 5.1 - Prob. 65SPRCh. 5.1 - Prob. 66SPRCh. 5.1 - Prob. 67SPRCh. 5.1 - Prob. 68SRCh. 5.1 - Prob. 69SRCh. 5.2 - Prob. 1ACYPCh. 5.2 - Prob. 1BCYPCh. 5.2 - Prob. 2ACYPCh. 5.2 - Prob. 2BCYPCh. 5.2 - Prob. 3CYPCh. 5.2 - Prob. 4CYPCh. 5.2 - Prob. 1CYUCh. 5.2 - Prob. 2CYUCh. 5.2 - Prob. 3CYUCh. 5.2 - Prob. 4CYUCh. 5.2 - Prob. 5PPSCh. 5.2 - Prob. 6PPSCh. 5.2 - Prob. 7PPSCh. 5.2 - Prob. 8PPSCh. 5.2 - Prob. 9PPSCh. 5.2 - Prob. 10PPSCh. 5.2 - Prob. 11PPSCh. 5.2 - Prob. 12PPSCh. 5.2 - Prob. 13PPSCh. 5.2 - Prob. 14PPSCh. 5.2 - Prob. 15PPSCh. 5.2 - Prob. 16PPSCh. 5.2 - Prob. 17PPSCh. 5.2 - Prob. 18PPSCh. 5.2 - Prob. 19PPSCh. 5.2 - Prob. 20PPSCh. 5.2 - Prob. 21PPSCh. 5.2 - Prob. 22PPSCh. 5.2 - Prob. 23PPSCh. 5.2 - Prob. 24PPSCh. 5.2 - Prob. 25PPSCh. 5.2 - Prob. 26PPSCh. 5.2 - Prob. 27PPSCh. 5.2 - Prob. 28PPSCh. 5.2 - Prob. 29PPSCh. 5.2 - Prob. 30PPSCh. 5.2 - Prob. 31PPSCh. 5.2 - Prob. 32PPSCh. 5.2 - Prob. 33PPSCh. 5.2 - Prob. 34PPSCh. 5.2 - Prob. 35PPSCh. 5.2 - Prob. 36PPSCh. 5.2 - Prob. 37HPCh. 5.2 - Prob. 38HPCh. 5.2 - Prob. 39HPCh. 5.2 - Prob. 40HPCh. 5.2 - Prob. 41HPCh. 5.2 - Prob. 42HPCh. 5.2 - Prob. 43HPCh. 5.2 - Prob. 44STPCh. 5.2 - Prob. 45STPCh. 5.2 - Prob. 46STPCh. 5.2 - Prob. 47STPCh. 5.2 - Prob. 48SPRCh. 5.2 - Prob. 49SPRCh. 5.2 - Prob. 50SPRCh. 5.2 - Prob. 51SPRCh. 5.2 - Prob. 52SPRCh. 5.2 - Prob. 53SPRCh. 5.2 - Prob. 54SPRCh. 5.2 - Prob. 55SPRCh. 5.2 - Prob. 56SRCh. 5.3 - Prob. 1ACYPCh. 5.3 - Prob. 1BCYPCh. 5.3 - Prob. 2CYPCh. 5.3 - Prob. 3CYPCh. 5.3 - Prob. 4CYPCh. 5.3 - Prob. 1CYUCh. 5.3 - Prob. 2CYUCh. 5.3 - Prob. 3CYUCh. 5.3 - Prob. 4CYUCh. 5.3 - Prob. 5CYUCh. 5.3 - Prob. 6CYUCh. 5.3 - Prob. 7CYUCh. 5.3 - Prob. 8PPSCh. 5.3 - Prob. 9PPSCh. 5.3 - Prob. 10PPSCh. 5.3 - Prob. 11PPSCh. 5.3 - Prob. 12PPSCh. 5.3 - Prob. 13PPSCh. 5.3 - Prob. 14PPSCh. 5.3 - Prob. 15PPSCh. 5.3 - Prob. 16PPSCh. 5.3 - Prob. 17PPSCh. 5.3 - Prob. 18PPSCh. 5.3 - Prob. 19PPSCh. 5.3 - Prob. 20PPSCh. 5.3 - Prob. 21PPSCh. 5.3 - Prob. 22PPSCh. 5.3 - Prob. 23PPSCh. 5.3 - Prob. 24PPSCh. 5.3 - Prob. 25PPSCh. 5.3 - Prob. 26PPSCh. 5.3 - Prob. 27PPSCh. 5.3 - Prob. 28PPSCh. 5.3 - Prob. 29PPSCh. 5.3 - Prob. 30PPSCh. 5.3 - Prob. 31PPSCh. 5.3 - Prob. 32PPSCh. 5.3 - Prob. 33PPSCh. 5.3 - Prob. 34PPSCh. 5.3 - Prob. 35PPSCh. 5.3 - Prob. 36PPSCh. 5.3 - Prob. 37PPSCh. 5.3 - Prob. 38PPSCh. 5.3 - Prob. 39PPSCh. 5.3 - Prob. 40PPSCh. 5.3 - Prob. 41PPSCh. 5.3 - Prob. 42PPSCh. 5.3 - Prob. 43HPCh. 5.3 - Prob. 44HPCh. 5.3 - Prob. 45HPCh. 5.3 - Prob. 46HPCh. 5.3 - Prob. 47HPCh. 5.3 - Prob. 48HPCh. 5.3 - Prob. 49STPCh. 5.3 - Prob. 50STPCh. 5.3 - Prob. 51STPCh. 5.3 - Prob. 52STPCh. 5.3 - Prob. 53SPRCh. 5.3 - Prob. 54SPRCh. 5.3 - Prob. 55SPRCh. 5.3 - Prob. 56SPRCh. 5.3 - Prob. 57SPRCh. 5.3 - Prob. 58SPRCh. 5.3 - Prob. 59SRCh. 5.3 - Prob. 60SRCh. 5.3 - Prob. 61SRCh. 5.4 - Prob. 1ACYPCh. 5.4 - Prob. 1BCYPCh. 5.4 - Prob. 1CCYPCh. 5.4 - Prob. 2ACYPCh. 5.4 - Prob. 2BCYPCh. 5.4 - Prob. 3CYPCh. 5.4 - Prob. 4CYPCh. 5.4 - Prob. 5CYPCh. 5.4 - Prob. 1CYUCh. 5.4 - Prob. 2CYUCh. 5.4 - Prob. 3CYUCh. 5.4 - Prob. 4CYUCh. 5.4 - Prob. 5CYUCh. 5.4 - Prob. 6CYUCh. 5.4 - Prob. 7CYUCh. 5.4 - Prob. 8CYUCh. 5.4 - Prob. 9CYUCh. 5.4 - Prob. 10CYUCh. 5.4 - Prob. 11PPSCh. 5.4 - Prob. 12PPSCh. 5.4 - Prob. 13PPSCh. 5.4 - Prob. 14PPSCh. 5.4 - Prob. 15PPSCh. 5.4 - Prob. 16PPSCh. 5.4 - Prob. 17PPSCh. 5.4 - Prob. 18PPSCh. 5.4 - Prob. 19PPSCh. 5.4 - Prob. 20PPSCh. 5.4 - Prob. 21PPSCh. 5.4 - Prob. 22PPSCh. 5.4 - Prob. 23PPSCh. 5.4 - Prob. 24PPSCh. 5.4 - Prob. 25PPSCh. 5.4 - Prob. 26PPSCh. 5.4 - Prob. 27PPSCh. 5.4 - Prob. 28PPSCh. 5.4 - Prob. 29PPSCh. 5.4 - Prob. 30PPSCh. 5.4 - Prob. 31PPSCh. 5.4 - Prob. 32PPSCh. 5.4 - Prob. 33PPSCh. 5.4 - Prob. 34PPSCh. 5.4 - Prob. 35PPSCh. 5.4 - Prob. 36PPSCh. 5.4 - Prob. 37PPSCh. 5.4 - Prob. 38PPSCh. 5.4 - Prob. 39PPSCh. 5.4 - Prob. 40HPCh. 5.4 - Prob. 41HPCh. 5.4 - Prob. 42HPCh. 5.4 - Prob. 43HPCh. 5.4 - Prob. 44HPCh. 5.4 - Prob. 45STPCh. 5.4 - Prob. 46STPCh. 5.4 - Prob. 47STPCh. 5.4 - Prob. 48STPCh. 5.4 - Prob. 49SPRCh. 5.4 - Prob. 50SPRCh. 5.4 - Prob. 51SPRCh. 5.4 - Prob. 52SPRCh. 5.4 - Prob. 53SPRCh. 5.4 - Prob. 54SPRCh. 5.4 - Prob. 55SPRCh. 5.4 - Prob. 56SPRCh. 5.4 - Prob. 57SRCh. 5.4 - Prob. 58SRCh. 5.4 - Prob. 59SRCh. 5.5 - Prob. 1ACYPCh. 5.5 - Prob. 1BCYPCh. 5.5 - Prob. 2CYPCh. 5.5 - Prob. 3CYPCh. 5.5 - Prob. 1CYUCh. 5.5 - Prob. 2CYUCh. 5.5 - Prob. 3CYUCh. 5.5 - Prob. 4CYUCh. 5.5 - Prob. 5CYUCh. 5.5 - Prob. 6PPSCh. 5.5 - Prob. 7PPSCh. 5.5 - Prob. 8PPSCh. 5.5 - Prob. 9PPSCh. 5.5 - Prob. 10PPSCh. 5.5 - Prob. 11PPSCh. 5.5 - Prob. 12PPSCh. 5.5 - Prob. 13PPSCh. 5.5 - Prob. 14PPSCh. 5.5 - Prob. 15PPSCh. 5.5 - Prob. 16PPSCh. 5.5 - Prob. 17PPSCh. 5.5 - Prob. 18PPSCh. 5.5 - Prob. 19PPSCh. 5.5 - Prob. 20PPSCh. 5.5 - Prob. 21PPSCh. 5.5 - Prob. 22PPSCh. 5.5 - Prob. 23PPSCh. 5.5 - Prob. 24PPSCh. 5.5 - Prob. 25PPSCh. 5.5 - Prob. 26PPSCh. 5.5 - Prob. 27PPSCh. 5.5 - Prob. 28PPSCh. 5.5 - Prob. 29PPSCh. 5.5 - Prob. 30PPSCh. 5.5 - Prob. 31PPSCh. 5.5 - Prob. 32PPSCh. 5.5 - Prob. 33PPSCh. 5.5 - Prob. 34PPSCh. 5.5 - Prob. 35PPSCh. 5.5 - Prob. 36PPSCh. 5.5 - Prob. 37PPSCh. 5.5 - Prob. 38PPSCh. 5.5 - Prob. 39PPSCh. 5.5 - Prob. 40PPSCh. 5.5 - Prob. 41PPSCh. 5.5 - Prob. 42PPSCh. 5.5 - Prob. 43HPCh. 5.5 - Prob. 44HPCh. 5.5 - Prob. 45HPCh. 5.5 - Prob. 46HPCh. 5.5 - Prob. 47HPCh. 5.5 - Prob. 48HPCh. 5.5 - Prob. 49STPCh. 5.5 - Prob. 50STPCh. 5.5 - Prob. 51STPCh. 5.5 - Prob. 52STPCh. 5.5 - Prob. 53SPRCh. 5.5 - Prob. 54SPRCh. 5.5 - Prob. 55SPRCh. 5.5 - Prob. 56SPRCh. 5.5 - Prob. 57SPRCh. 5.5 - Prob. 58SPRCh. 5.5 - Prob. 59SPRCh. 5.5 - Prob. 60SPRCh. 5.5 - Prob. 61SRCh. 5.5 - Prob. 62SRCh. 5.5 - Prob. 63SRCh. 5.6 - Prob. 1ACYPCh. 5.6 - Prob. 1BCYPCh. 5.6 - Prob. 2ACYPCh. 5.6 - Prob. 2BCYPCh. 5.6 - Prob. 3CYPCh. 5.6 - Prob. 4CYPCh. 5.6 - Prob. 5CYPCh. 5.6 - Prob. 1CYUCh. 5.6 - Prob. 2CYUCh. 5.6 - Prob. 3CYUCh. 5.6 - Prob. 4CYUCh. 5.6 - Prob. 5CYUCh. 5.6 - Prob. 6CYUCh. 5.6 - Prob. 7CYUCh. 5.6 - Prob. 8CYUCh. 5.6 - Prob. 9CYUCh. 5.6 - Prob. 10PPSCh. 5.6 - Prob. 11PPSCh. 5.6 - Prob. 12PPSCh. 5.6 - Prob. 13PPSCh. 5.6 - Prob. 14PPSCh. 5.6 - Prob. 15PPSCh. 5.6 - Prob. 16PPSCh. 5.6 - Prob. 17PPSCh. 5.6 - Prob. 18PPSCh. 5.6 - Prob. 19PPSCh. 5.6 - Prob. 20PPSCh. 5.6 - Prob. 21PPSCh. 5.6 - Prob. 22PPSCh. 5.6 - Prob. 23PPSCh. 5.6 - Prob. 24PPSCh. 5.6 - Prob. 25PPSCh. 5.6 - Prob. 26PPSCh. 5.6 - Prob. 27PPSCh. 5.6 - Prob. 28PPSCh. 5.6 - Prob. 29PPSCh. 5.6 - Prob. 30PPSCh. 5.6 - Prob. 31PPSCh. 5.6 - Prob. 32PPSCh. 5.6 - Prob. 33PPSCh. 5.6 - Prob. 34PPSCh. 5.6 - Prob. 35PPSCh. 5.6 - Prob. 36PPSCh. 5.6 - Prob. 37PPSCh. 5.6 - Prob. 38HPCh. 5.6 - Prob. 39HPCh. 5.6 - Prob. 40HPCh. 5.6 - Prob. 41HPCh. 5.6 - Prob. 42HPCh. 5.6 - Prob. 43STPCh. 5.6 - Prob. 44STPCh. 5.6 - Prob. 45STPCh. 5.6 - Prob. 46STPCh. 5.6 - Prob. 47SPRCh. 5.6 - Prob. 48SPRCh. 5.6 - Prob. 49SPRCh. 5.6 - Prob. 50SPRCh. 5.6 - Prob. 51SPRCh. 5.6 - Prob. 52SPRCh. 5.6 - Prob. 53SPRCh. 5.6 - Prob. 54SPRCh. 5.6 - Prob. 55SPRCh. 5.6 - Prob. 56SRCh. 5.6 - Prob. 57SRCh. 5.6 - Prob. 58SRCh. 5 - Prob. 1GRFCCh. 5 - Prob. 2GRFCCh. 5 - Prob. 3GRFCCh. 5 - Prob. 4GRFCCh. 5 - Prob. 5GRFCCh. 5 - Prob. 6GRFCCh. 5 - Prob. 7GRFCCh. 5 - Prob. 8GRFCCh. 5 - Prob. 9GRFCCh. 5 - Prob. 10GRFCCh. 5 - Prob. 11GRFCCh. 5 - Prob. 12GRFCCh. 5 - Prob. 1MCQCh. 5 - Prob. 2MCQCh. 5 - Prob. 3MCQCh. 5 - Prob. 4MCQCh. 5 - Prob. 5MCQCh. 5 - Prob. 6MCQCh. 5 - Prob. 7MCQCh. 5 - Prob. 8MCQCh. 5 - Prob. 9MCQCh. 5 - Prob. 10MCQCh. 5 - Prob. 11MCQCh. 5 - Prob. 12MCQCh. 5 - Prob. 13MCQCh. 5 - Prob. 14MCQCh. 5 - Prob. 15MCQCh. 5 - Prob. 16MCQCh. 5 - Prob. 17MCQCh. 5 - Prob. 18MCQCh. 5 - Prob. 19MCQCh. 5 - Prob. 1SGRCh. 5 - Prob. 2SGRCh. 5 - Prob. 3SGRCh. 5 - Prob. 4SGRCh. 5 - Prob. 5SGRCh. 5 - Prob. 6SGRCh. 5 - Prob. 7SGRCh. 5 - Prob. 8SGRCh. 5 - Prob. 9SGRCh. 5 - Prob. 10SGRCh. 5 - Prob. 11SGRCh. 5 - Prob. 12SGRCh. 5 - Prob. 13SGRCh. 5 - Prob. 14SGRCh. 5 - Prob. 15SGRCh. 5 - Prob. 16SGRCh. 5 - Prob. 17SGRCh. 5 - Prob. 18SGRCh. 5 - Prob. 19SGRCh. 5 - Prob. 20SGRCh. 5 - Prob. 21SGRCh. 5 - Prob. 22SGRCh. 5 - Prob. 23SGRCh. 5 - Prob. 24SGRCh. 5 - Prob. 25SGRCh. 5 - Prob. 26SGRCh. 5 - Prob. 27SGRCh. 5 - Prob. 28SGRCh. 5 - Prob. 29SGRCh. 5 - Prob. 30SGRCh. 5 - Prob. 31SGRCh. 5 - Prob. 32SGRCh. 5 - Prob. 33SGRCh. 5 - Prob. 1PTCh. 5 - Prob. 2PTCh. 5 - Prob. 3PTCh. 5 - Prob. 4PTCh. 5 - Prob. 5PTCh. 5 - Prob. 6PTCh. 5 - Prob. 7PTCh. 5 - Prob. 8PTCh. 5 - Prob. 9PTCh. 5 - Prob. 10PTCh. 5 - Prob. 11PTCh. 5 - Prob. 12PTCh. 5 - Prob. 13PTCh. 5 - Prob. 14PTCh. 5 - Prob. 15PTCh. 5 - Prob. 16PTCh. 5 - Prob. 17PTCh. 5 - Prob. 18PTCh. 5 - Prob. 19PTCh. 5 - Prob. 20PTCh. 5 - Prob. 21PTCh. 5 - Prob. 22PTCh. 5 - Prob. 23PTCh. 5 - Prob. 24PTCh. 5 - Prob. 25PTCh. 5 - Prob. 1ECh. 5 - Prob. 2ECh. 5 - Prob. 3ECh. 5 - Prob. 4ECh. 5 - Prob. 5ECh. 5 - Prob. 1STPCh. 5 - Prob. 2STPCh. 5 - Prob. 3STPCh. 5 - Prob. 4STPCh. 5 - Prob. 5STPCh. 5 - Prob. 6STPCh. 5 - Prob. 7STPCh. 5 - Prob. 8STPCh. 5 - Prob. 9STPCh. 5 - Prob. 10STPCh. 5 - Prob. 11STPCh. 5 - Prob. 12STPCh. 5 - Prob. 13STPCh. 5 - Prob. 14STPCh. 5 - Prob. 15STP
Additional Math Textbook Solutions
Find more solutions based on key concepts
Fill in each blank so that the resulting statement is true. The quadratic function f(x)=a(xh)2+k,a0, is in ____...
Algebra and Trigonometry (6th Edition)
Confidence Intervals. In Exercises 9–24, construct the confidence interval estimate of the mean.
12. Atkins Wei...
Elementary Statistics (13th Edition)
In Exercises 9–22, write the function in the form y = f(u) and u = g(x). Then find dy/dx as a function of x.
13...
University Calculus: Early Transcendentals (4th Edition)
The following set of data is from sample of n=5: a. Compute the mean, median, and mode. b. Compute the range, v...
Basic Business Statistics, Student Value Edition
TRY IT YOURSELF 1
Find the mean of the points scored by the 51 winning teams listed on page 39.
Elementary Statistics: Picturing the World (7th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Can someone help me with this please?arrow_forwardMariela is in her classroom and looking out of a window at a tree, which is 20 feet away. Mariela’s line of sight to the top of the tree creates a 42° angle of elevation, and her line of sight to the base of the tree creates a 31° angle of depression. What is the height of the tree, rounded to the nearest foot? Be sure to show your work to explain how you got your answer.arrow_forward1arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Quadrilaterals: Missing Angles and Sides; Author: rhornfeck;https://www.youtube.com/watch?v=knVj1O0L2TM;License: Standard YouTube License, CC-BY
STD IX | State Board | Types of Quadrilateral; Author: Robomate;https://www.youtube.com/watch?v=wh0KQ4UB0EU;License: Standard YouTube License, CC-BY