
Calculus: Early Transcendentals (3rd Edition)
3rd Edition
ISBN: 9780134770468
Author: Briggs
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 5.1, Problem 43E
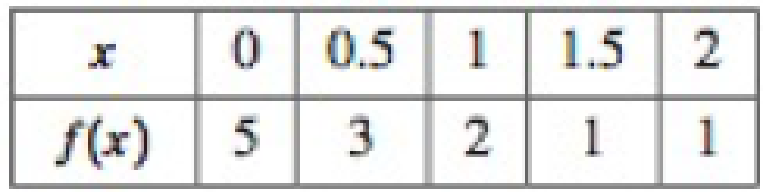
Riemann sums from tables Evaluate the left and right Riemann sums for f over the given interval for the given value of n.
35. n = 4; [0, 2]
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
(x)=2x-x2
2
a=2, b = 1/2, C=0
b) Vertex v
F(x)=ax 2 + bx + c
x=
Za
V=2.0L
YEF(- =) = 4
b
(글)
JANUARY 17, 2025
WORKSHEET 1
Solve the following four problems on a separate sheet. Fully justify your answers to
MATH 122
ล
T
earn full credit.
1. Let f(x) = 2x-
1x2
2
(a) Rewrite this quadratic function in standard form: f(x) = ax² + bx + c
and indicate the values of the coefficients: a, b and c.
(b) Find the vertex V, focus F, focal width, directrix D, and the axis of
symmetry for the graph of y = f(x).
(c) Plot a graph of y = f(x) and indicate all quantities found in part (b)
on your graph.
(d) Specify the domain and range of the function f.
OUR
2. Let g(x) = f(x) u(x) where f is the quadratic function from problem 1
and u is the unit step function:
u(x) = { 0
1 if x ≥0
0 if x<0
y = u(x)
0
(a) Write a piecewise formula for the function g.
(b) Sketch a graph of y = g(x).
(c) Indicate the domain and range of the function g.
X
фирм
where u is the unit step function defined in problem 2.
3. Let…
Question 1
"P3
Question 3: Construct the accessibility matrix Passociated with
the following graphs, and compute P2 and identify each at the
various two-step paths in the graph
Ps
P₁
P₂
Chapter 5 Solutions
Calculus: Early Transcendentals (3rd Edition)
Ch. 5.1 - What is the displacement of an object that travels...Ch. 5.1 - In Example 1, if we used n = 32 subintervals of...Ch. 5.1 - If the interval [1, 9] is partitioned into 4...Ch. 5.1 - If the function in Example 2 is replaced with f(x)...Ch. 5.1 - Suppose an object moves along a line at 15 m/s,...Ch. 5.1 - Given the graph of the positive velocity of an...Ch. 5.1 - Prob. 3ECh. 5.1 - The velocity in ft/s or an object moving along a...Ch. 5.1 - The velocity in ft/s of an object moving along a...Ch. 5.1 - The velocity in ft/s of an object moving along a...
Ch. 5.1 - Prob. 7ECh. 5.1 - Explain how Riemann sum approximations to the area...Ch. 5.1 - Prob. 9ECh. 5.1 - Prob. 10ECh. 5.1 - Suppose the interval [1, 3] is partitioned into n...Ch. 5.1 - Prob. 12ECh. 5.1 - Does a right Riemann sum underestimate or...Ch. 5.1 - Does a left Riemann sum underestimate or...Ch. 5.1 - Approximating displacement The velocity in ft/s of...Ch. 5.1 - Approximating displacement The velocity in ft/s of...Ch. 5.1 - Approximating displacement The velocity of an...Ch. 5.1 - Approximating displacement The velocity of an...Ch. 5.1 - Approximating displacement The velocity of an...Ch. 5.1 - Approximating displacement The velocity of an...Ch. 5.1 - Approximating displacement The velocity of an...Ch. 5.1 - Approximating displacement The velocity of an...Ch. 5.1 - Prob. 23ECh. 5.1 - Prob. 24ECh. 5.1 - Prob. 25ECh. 5.1 - Prob. 26ECh. 5.1 - Prob. 27ECh. 5.1 - Prob. 28ECh. 5.1 - Prob. 29ECh. 5.1 - Prob. 30ECh. 5.1 - Prob. 31ECh. 5.1 - Prob. 32ECh. 5.1 - A midpoint Riemann sum Approximate the area of the...Ch. 5.1 - Prob. 34ECh. 5.1 - Free fall On October 14, 2012, Felix Baumgartner...Ch. 5.1 - Free fall Use geometry and the figure given in...Ch. 5.1 - Prob. 37ECh. 5.1 - Midpoint Riemann sums Complete the following steps...Ch. 5.1 - Prob. 39ECh. 5.1 - Prob. 40ECh. 5.1 - Prob. 41ECh. 5.1 - Prob. 42ECh. 5.1 - Riemann sums from tables Evaluate the left and...Ch. 5.1 - Prob. 44ECh. 5.1 - Displacement from a table of velocities The...Ch. 5.1 - Displacement from a table of velocities The...Ch. 5.1 - Sigma notation Express the following sums using...Ch. 5.1 - Sigma notation Express the following sums using...Ch. 5.1 - Sigma notation Evaluate the following expressions....Ch. 5.1 - Evaluating sums Evaluate the following expressions...Ch. 5.1 - Prob. 51ECh. 5.1 - Prob. 52ECh. 5.1 - Prob. 53ECh. 5.1 - Prob. 54ECh. 5.1 - Prob. 55ECh. 5.1 - Prob. 56ECh. 5.1 - Prob. 57ECh. 5.1 - Prob. 58ECh. 5.1 - Explain why or why not Determine whether the...Ch. 5.1 - Prob. 60ECh. 5.1 - Prob. 61ECh. 5.1 - Prob. 62ECh. 5.1 - Prob. 63ECh. 5.1 - Prob. 64ECh. 5.1 - Identifying Riemann sums Fill in the blanks with...Ch. 5.1 - Identifying Riemann sums Fill in the blanks with...Ch. 5.1 - Prob. 67ECh. 5.1 - Prob. 68ECh. 5.1 - Approximating areas Estimate the area of the...Ch. 5.1 - Displacement from a velocity graph Consider the...Ch. 5.1 - Displacement from a velocity graph Consider the...Ch. 5.1 - Flow rates Suppose a gauge at the outflow of a...Ch. 5.1 - Mass from density A thin 10-cm rod is made of an...Ch. 5.1 - Prob. 74ECh. 5.1 - Prob. 75ECh. 5.1 - Prob. 76ECh. 5.1 - Prob. 77ECh. 5.1 - Riemann sums for constant functions Let f(x) = c,...Ch. 5.1 - Prob. 79ECh. 5.1 - Prob. 80ECh. 5.1 - Prob. 81ECh. 5.2 - Suppose f(x) = 5. What is the net area of the...Ch. 5.2 - Sketch a continuous function f that is positive...Ch. 5.2 - Graph f(x) = x and use geometry to evaluate 11xdx.Ch. 5.2 - Let f(x) = 5 and use geometry to evaluate...Ch. 5.2 - Evaluate abf(x)dx+baf(x)dx assuming f is integrate...Ch. 5.2 - Evaluate 12xdx and 12|x|dx using geometry.Ch. 5.2 - What does net area measure?Ch. 5.2 - Under what conditions does the net area of a...Ch. 5.2 - Prob. 3ECh. 5.2 - Use the graph of y = g(x) to estimate 210g(x)dx...Ch. 5.2 - Suppose f is continuous on [2, 8]. Use the table...Ch. 5.2 - Suppose g is continuous on [1, 9]. Use the table...Ch. 5.2 - Sketch a graph of y = 2 on [1, 4] and use geometry...Ch. 5.2 - Sketch a graph of y = 3 on [1, 5] and use geometry...Ch. 5.2 - Sketch a graph of y = 2x on [1, 2] and use...Ch. 5.2 - Suppose 13f(x)dx=10 and 13g(x)dx=20. Evaluate...Ch. 5.2 - Use graphs to evaluate 02sinxdx and 02cosxdx.Ch. 5.2 - Explain how the notation for Riemann sums,...Ch. 5.2 - Give a geometrical explanation of why aaf(x)dx=0.Ch. 5.2 - Use Table 5.4 to rewrite 16(2x34x)dx as the...Ch. 5.2 - Use geometry to find a formula for 0axdx, in terms...Ch. 5.2 - If f is continuous on [a, b] and abf(x)dx=0, what...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Approximating net area The following functions are...Ch. 5.2 - Prob. 27ECh. 5.2 - Prob. 28ECh. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Approximating definite integrals Complete the...Ch. 5.2 - Approximating definite integrals Complete the...Ch. 5.2 - Approximating definite integrals Complete the...Ch. 5.2 - Approximating definite integrals Complete the...Ch. 5.2 - Prob. 35ECh. 5.2 - Prob. 36ECh. 5.2 - Identifying definite integrals as limits of sums...Ch. 5.2 - Prob. 38ECh. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area and definite integrals Use geometry (not...Ch. 5.2 - Net area from graphs The accompanying figure shows...Ch. 5.2 - Net area from graphs The accompanying figure shows...Ch. 5.2 - Net area from graphs The accompanying figure shows...Ch. 5.2 - Net area from graphs The accompanying figure shows...Ch. 5.2 - Properties of integrals Use only the fact that...Ch. 5.2 - Properties of integrals Suppose 14f(x)dx=8 and...Ch. 5.2 - Properties of integrals Suppose 03f(x)dx=2,...Ch. 5.2 - Properties of integrals Suppose f(x) 0 on [0, 2],...Ch. 5.2 - More properties of integrals Consider two...Ch. 5.2 - Suppose f is continuous on [1, 5] and 2 f(x) 3...Ch. 5.2 - Using properties of integrals Use the value of the...Ch. 5.2 - Using properties of integrals Use the value of the...Ch. 5.2 - Net area from graphs The figure shows the areas of...Ch. 5.2 - Net area from graphs The figure shows the areas of...Ch. 5.2 - Net area from graphs The figure shows the areas of...Ch. 5.2 - Net area from graphs The figure shows the areas of...Ch. 5.2 - Definite integrals from graphs The figure shows...Ch. 5.2 - Definite integrals from graphs The figure shows...Ch. 5.2 - Definite integrals from graphs The figure shows...Ch. 5.2 - Definite integrals from graphs The figure shows...Ch. 5.2 - Use geometry and properties of integrals to...Ch. 5.2 - Use geometry and properties of integrals to...Ch. 5.2 - Explain why or why not Determine whether the...Ch. 5.2 - Approximating definite integrals with a calculator...Ch. 5.2 - Approximating definite integrals with a calculator...Ch. 5.2 - Approximating definite integrals with a calculator...Ch. 5.2 - Approximating definite integrals with a calculator...Ch. 5.2 - Approximating definite integrals with a calculator...Ch. 5.2 - Midpoint Riemann sums with a calculator Consider...Ch. 5.2 - Midpoint Riemann sums with a calculator Consider...Ch. 5.2 - Midpoint Riemann sums with a calculator Consider...Ch. 5.2 - Midpoint Riemann sums with a calculator Consider...Ch. 5.2 - Limits of sums Use the definition of the definite...Ch. 5.2 - Limits of sums Use the definition of the definite...Ch. 5.2 - Limits of sums Use the definition of the definite...Ch. 5.2 - Limits of sums Use the definition of the definite...Ch. 5.2 - Limits of sums Use the definition of the definite...Ch. 5.2 - Limits of sums Use the definition of the definite...Ch. 5.2 - Limits of sums Use the definition of the definite...Ch. 5.2 - Area by geometry Use geometry to evaluate the...Ch. 5.2 - Area by geometry Use geometry to evaluate the...Ch. 5.2 - Integrating piecewise continuous functions Suppose...Ch. 5.2 - Integrating piecewise continuous functions Use...Ch. 5.2 - Integrating piecewise continuous functions Use...Ch. 5.2 - Integrating piecewise continuous functions Recall...Ch. 5.2 - Integrating piecewise continuous functions Recall...Ch. 5.2 - Constants in integrals Use the definition of the...Ch. 5.2 - Zero net area If 0 c d, then find the value of b...Ch. 5.2 - A nonintegrable function Consider the function...Ch. 5.2 - Powers of x by Riemann sums Consider the integral...Ch. 5.2 - An exact integration formula Evaluate abdxx2,...Ch. 5.2 - Use Property 3 of Table 5.4 and Property 7 of...Ch. 5.3 - In Example 1, let B(x) be the area function for f...Ch. 5.3 - Verify that the area function in Example 2c gives...Ch. 5.3 - Evaluate (xx+1)|12.Ch. 5.3 - Explain why f is an antiderivative of f.Ch. 5.3 - Suppose A is an area function of f. What is the...Ch. 5.3 - Suppose F is an antiderivative of f and A is an...Ch. 5.3 - Explain in words and write mathematically how the...Ch. 5.3 - Let f(x) = c, where c is a positive constant....Ch. 5.3 - The linear function f(x) = 3 x is decreasing on...Ch. 5.3 - Evaluate 023x2dx and 223x2dx.Ch. 5.3 - Explain in words and express mathematically the...Ch. 5.3 - Why can the constant of integration be omitted...Ch. 5.3 - Evaluate ddxaxf(t)dt and ddxabf(t)dt, where a and...Ch. 5.3 - Explain why abf(x)dx=f(b)f(a).Ch. 5.3 - Evaluate 38f(t)dt, where f is continuous on [3,...Ch. 5.3 - Evaluate 273dx using the Fundamental Theorem of...Ch. 5.3 - Prob. 13ECh. 5.3 - Area functions The graph of f is shown in the...Ch. 5.3 - Area functions for constant functions Consider the...Ch. 5.3 - Area functions for constant functions Consider the...Ch. 5.3 - Area functions for the same linear function Let...Ch. 5.3 - Area functions for the same linear function Let...Ch. 5.3 - Area functions for linear functions Consider the...Ch. 5.3 - Area functions for linear functions Consider the...Ch. 5.3 - Area functions for linear functions Consider the...Ch. 5.3 - Area functions for linear functions Consider the...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following definite...Ch. 5.3 - Definite integrals Evaluate the following definite...Ch. 5.3 - Definite integrals Evaluate the following definite...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following definite...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following definite...Ch. 5.3 - Definite integrals Evaluate the following definite...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Definite integrals Evaluate the following...Ch. 5.3 - Areas Find (i) the net area and (ii) the area of...Ch. 5.3 - Areas Find (i) the net area and (ii) the area of...Ch. 5.3 - Areas Find (i) the net area and (ii) the area of...Ch. 5.3 - Areas Find (i) the net area and (ii) the area of...Ch. 5.3 - Areas of regions Find the area of the region...Ch. 5.3 - Areas of regions Find the area of the region...Ch. 5.3 - Areas of regions Find the area of the region...Ch. 5.3 - Areas of regions Find the area of the region...Ch. 5.3 - Areas of regions Find the area of the region...Ch. 5.3 - Areas of regions Find the area of the region...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives and integrals Simplify the given...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives and integrals Simplify the given...Ch. 5.3 - Derivatives and integrals Simplify the given...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives and integrals Simplify the given...Ch. 5.3 - Derivatives and integrals Simplify the given...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Derivatives of integrals Simplify the following...Ch. 5.3 - Prob. 87ECh. 5.3 - Working with area functions Consider the function...Ch. 5.3 - Prob. 89ECh. 5.3 - Prob. 90ECh. 5.3 - Prob. 91ECh. 5.3 - Prob. 92ECh. 5.3 - Area functions from graphs The graph of f is given...Ch. 5.3 - Prob. 94ECh. 5.3 - Working with area functions Consider the function...Ch. 5.3 - Working with area functions Consider the function...Ch. 5.3 - Prob. 97ECh. 5.3 - Prob. 98ECh. 5.3 - Find the critical points of the function...Ch. 5.3 - Determine the intervals on which the function...Ch. 5.3 - Prob. 101ECh. 5.3 - Prob. 102ECh. 5.3 - Areas of regions Find the area of the region R...Ch. 5.3 - Prob. 104ECh. 5.3 - Areas of regions Find the area of the region R...Ch. 5.3 - Areas of regions Find the area of the region R...Ch. 5.3 - Explain why or why not Determine whether the...Ch. 5.3 - Explorations and Challenges Evaluate...Ch. 5.3 - Maximum net area What value of b 1 maximizes the...Ch. 5.3 - Maximum net area Graph the function f(x) = 8 + 2x ...Ch. 5.3 - Prob. 111ECh. 5.3 - Cubic zero net area Consider the graph of the...Ch. 5.3 - An integral equation Use the Fundamental Theorem...Ch. 5.3 - Prob. 114ECh. 5.3 - Asymptote of sine integral Use a calculator to...Ch. 5.3 - Sine integral Show that the sine integral...Ch. 5.3 - Prob. 117ECh. 5.3 - Continuity at the endpoints Assume that f is...Ch. 5.3 - Discrete version of the Fundamental Theorem In...Ch. 5.4 - If f and g are both even functions, is the product...Ch. 5.4 - Prob. 2QCCh. 5.4 - Explain why f(x) = 0 for at least one point of (a,...Ch. 5.4 - If f is an odd function, why is aaf(x)dx=0?Ch. 5.4 - If f is an even function, why is...Ch. 5.4 - Using symmetry Suppose f is an even function and...Ch. 5.4 - Using symmetry Suppose f is an odd function,...Ch. 5.4 - Use symmetry to explain why...Ch. 5.4 - Use symmetry to fill in the blanks:...Ch. 5.4 - Is x12 an even or odd function? Is sin x2 an even...Ch. 5.4 - Prob. 8ECh. 5.4 - Prob. 9ECh. 5.4 - Prob. 10ECh. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Symmetry in integrals Use symmetry to evaluate the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average values Find the average value of the...Ch. 5.4 - Average distance on a parabola What is the average...Ch. 5.4 - Average elevation The elevation of a path is given...Ch. 5.4 - Average velocity The velocity in m/s of an object...Ch. 5.4 - Average velocity A rock is launched vertically...Ch. 5.4 - Average height of an arch The height of an arch...Ch. 5.4 - Average height of a wave The surface of a water...Ch. 5.4 - Mean Value Theorem for Integrals Find or...Ch. 5.4 - Mean Value Theorem for Integrals Find or...Ch. 5.4 - Mean Value Theorem for Integrals Find or...Ch. 5.4 - Mean Value Theorem for Integrals Find or...Ch. 5.4 - Mean Value Theorem for Integrals Find or...Ch. 5.4 - Mean Value Theorem for Integrals Find or...Ch. 5.4 - Explain why or why not Determine whether the...Ch. 5.4 - Planetary orbits The planets orbit the Sun in...Ch. 5.4 - Gateway Arch The Gateway Arch in St. Louis is 630...Ch. 5.4 - Comparing a sine and a quadratic function Consider...Ch. 5.4 - Symmetry of composite functions Prove that the...Ch. 5.4 - Symmetry of composite functions Prove that the...Ch. 5.4 - Prob. 51ECh. 5.4 - Symmetry of composite functions Prove that the...Ch. 5.4 - Prob. 53ECh. 5.4 - Alternative definitions of means Consider the...Ch. 5.4 - Problems of antiquity Several calculus problems...Ch. 5.4 - Prob. 56ECh. 5.4 - Symmetry of powers Fill in the following table...Ch. 5.4 - Bounds on an integral Suppose f is continuous on...Ch. 5.4 - Generalizing the Mean Value Theorem for Integrals...Ch. 5.4 - A sine integral by Riemann sums Consider the...Ch. 5.5 - Find a new variable u so that 4x3(x4+5)10dx=u10du.Ch. 5.5 - In Example 2a, explain why the same substitution...Ch. 5.5 - Evaluate cos6xdxwithout using the substitution...Ch. 5.5 - Evaluate 44x2dx.Ch. 5.5 - Changes of variables occur frequently in...Ch. 5.5 - Review Questions 1. On which derivative rule is...Ch. 5.5 - Why is the Substitution Rule referred to as a...Ch. 5.5 - The composite function f(g(x)) consists of an...Ch. 5.5 - Find a suitable substitution for evaluating...Ch. 5.5 - When using a change of variables u = g(x) to...Ch. 5.5 - If the change of variables u = x2 4 is used to...Ch. 5.5 - Substitution given Use the given substitution to...Ch. 5.5 - Substitution given Use the given substitution to...Ch. 5.5 - Substitution given Use the given substitution to...Ch. 5.5 - Substitution given Use the given substitution to...Ch. 5.5 - Use a substitution of the form u = ax + b to...Ch. 5.5 - Use a substitution of the form u = ax + b to...Ch. 5.5 - Use a substitution of the form u = ax + b to...Ch. 5.5 - Use a substitution of the form u = ax + b to...Ch. 5.5 - Use Table 5.6 to evaluate the following indefinite...Ch. 5.5 - Use Table 5.6 to evaluate the following definite...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - x9sinx10dxCh. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - sec2(10x+7)dxCh. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Indefinite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - Definite integrals Use a change of variables or...Ch. 5.5 - 0ln4ex3+2exdxCh. 5.5 - 01x1x2dxCh. 5.5 - Prob. 66ECh. 5.5 - Prob. 67ECh. 5.5 - 06/5dx25x2+36Ch. 5.5 - 02x316x4dxCh. 5.5 - 11(x1)(x22x)7dxCh. 5.5 - 0sinx2+cosxdxCh. 5.5 - 01(v+1)(v+2)2v3+9v2+12v+36dvCh. 5.5 - 1249x2+6x+1dxCh. 5.5 - 0/4esin2xsin2xdxCh. 5.5 - Average velocity An object moves in one dimension...Ch. 5.5 - Periodic motion An object moves along a line with...Ch. 5.5 - Population models The population of a culture of...Ch. 5.5 - Variations on the substitution method Evaluate the...Ch. 5.5 - Variations on the substitution method Find the...Ch. 5.5 - Variations on the substitution method Find the...Ch. 5.5 - Variations on the substitution method Find the...Ch. 5.5 - Variations on the substitution method Find the...Ch. 5.5 - Variations on the substitution method Find the...Ch. 5.5 - Variations on the substitution method Find the...Ch. 5.5 - x(x+10)9dxCh. 5.5 - 033dx9+x2Ch. 5.5 - Integrals with sin2 x and cos2 x Evaluate the...Ch. 5.5 - Integrals with sin2 x and cos2 x Evaluate the...Ch. 5.5 - Integrals with sin2 x and cos2 x Evaluate the...Ch. 5.5 - Integrals with sin2 x and cos2 x Evaluate the...Ch. 5.5 - Integrals with sin2 x and cos2 x Evaluate the...Ch. 5.5 - Integrals with sin2 x and cos2 x Evaluate the...Ch. 5.5 - Integrals with sin2 x and cos2 x Evaluate the...Ch. 5.5 - Prob. 94ECh. 5.5 - Explain why or why not Determine whether the...Ch. 5.5 - Prob. 96ECh. 5.5 - Prob. 97ECh. 5.5 - Areas of regions Find the area of the following...Ch. 5.5 - Prob. 99ECh. 5.5 - Prob. 100ECh. 5.5 - Substitutions Suppose that p is a nonzero real...Ch. 5.5 - Prob. 102ECh. 5.5 - Average value of sine functions Use a graphing...Ch. 5.5 - Equal areas The area of the shaded region under...Ch. 5.5 - Equal areas The area of the shaded region under...Ch. 5.5 - Prob. 106ECh. 5.5 - Prob. 107ECh. 5.5 - Prob. 108ECh. 5.5 - More than one way Occasionally, two different...Ch. 5.5 - Prob. 110ECh. 5.5 - Prob. 111ECh. 5.5 - sin2 ax and cos2 ax integrals Use the Substitution...Ch. 5.5 - Integral of sin2 x cos2 x Consider the integral...Ch. 5.5 - Substitution: shift Perhaps the simplest change of...Ch. 5.5 - Prob. 115ECh. 5.5 - Prob. 116ECh. 5.5 - Prob. 117ECh. 5.5 - Prob. 118ECh. 5.5 - Multiple substitutions If necessary, use two or...Ch. 5 - Explain why or why not Determine whether the...Ch. 5 - Prob. 2RECh. 5 - Ascent rate of a scuba diver Divers who ascend too...Ch. 5 - Use the tabulated values of f to estimate the...Ch. 5 - Estimate 144x+1dx by evaluating the left, right,...Ch. 5 - Prob. 6RECh. 5 - Estimating a definite integral Use a calculator...Ch. 5 - Suppose the expression lim0k=1n(xk3+xk)xk is the...Ch. 5 - Integration by Riemann sums Consider the integral...Ch. 5 - Limit definition of the definite integral Use the...Ch. 5 - Limit definition of the definite integral Use the...Ch. 5 - Limit definition of the definite integral Use the...Ch. 5 - Prob. 13RECh. 5 - Sum to integral Evaluate the following limit by...Ch. 5 - Symmetry properties Suppose that 04f(x)dx=10 and...Ch. 5 - Properties of integrals The figure shows the areas...Ch. 5 - Properties of integrals Suppose that 14f(x)dx=6,...Ch. 5 - Properties of integrals Suppose that 14f(x)dx=6,...Ch. 5 - Properties of integrals Suppose that 14f(x)dx=6,...Ch. 5 - Properties of integrals Suppose that 14f(x)dx=6,...Ch. 5 - Properties of integrals Suppose that 14f(x)dx=6,...Ch. 5 - Properties of integrals Suppose that 14f(x)dx=6,...Ch. 5 - Area by geometry Use geometry to evaluate the...Ch. 5 - Displacement by geometry Use geometry to find the...Ch. 5 - Area by geometry Use geometry to evaluate...Ch. 5 - Use geometry and properties of integrals to...Ch. 5 - Prob. 27RECh. 5 - Prob. 28RECh. 5 - Evaluate the following derivatives. 29....Ch. 5 - Evaluate the following derivatives....Ch. 5 - Evaluate the following derivatives. 31....Ch. 5 - Evaluate the following derivatives. 32....Ch. 5 - Evaluate the following derivatives. 33....Ch. 5 - Evaluate the following derivatives. 34....Ch. 5 - Find the intervals on which f(x)=x1(t3)(t6)11dt is...Ch. 5 - Area function by geometry Use geometry to find the...Ch. 5 - Given that F=f, use the substitution method to...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - 015re3r2+2drCh. 5 - sinzsin(cosz)dzCh. 5 - ex+exdxCh. 5 - Evaluating integrals Evaluate the following...Ch. 5 - dx14x2Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - 02cos2x6dxCh. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Prob. 71RECh. 5 - 33(511x17+302x13+117x9+303x3+x2)dxCh. 5 - 1x2sin1xdxCh. 5 - (tan1x)51+x2dxCh. 5 - dx(tan1x)(1+x2)Ch. 5 - sin1x1x2dxCh. 5 - x(x+3)10dxCh. 5 - x7x4+1dxCh. 5 - Evaluating integrals Evaluate the following...Ch. 5 - Evaluating integrals Evaluate the following...Ch. 5 - 2/52/5dxx25x21Ch. 5 - sin2x1+cos2xdx (Hint: sin2x=2sinxcosx.)Ch. 5 - 1010x200x2dxCh. 5 - /2/2(cos2x+cosxsinx3sinx5)dxCh. 5 - 04f(x)dx for f(x)={2x+1ifx33x2+2x8ifx3Ch. 5 - 05|2x8|dxCh. 5 - Prob. 87RECh. 5 - Area of regions Compute the area of the region...Ch. 5 - Prob. 89RECh. 5 - Prob. 90RECh. 5 - Prob. 91RECh. 5 - Area versus net area Find (i) the net area and...Ch. 5 - Gateway Arch The Gateway Arch in St Louis is 630...Ch. 5 - Root mean square The root mean square (or RMS) is...Ch. 5 - Displacement from velocity A particle moves along...Ch. 5 - Velocity to displacement An object travels on the...Ch. 5 - Find the average value of f(x)=e2xon [0, ln 2].Ch. 5 - Average height A baseball is launched into the...Ch. 5 - Average values Integration is not needed. a. Find...Ch. 5 - Prob. 100RECh. 5 - An unknown function Assume f is continuous on [2,...Ch. 5 - Prob. 102RECh. 5 - Prob. 103RECh. 5 - Change of variables Use the change of variables u3...Ch. 5 - Prob. 105RECh. 5 - Area functions and the Fundamental Theorem...Ch. 5 - Limits with integrals Evaluate the following...Ch. 5 - Limits with integrals Evaluate the following...Ch. 5 - Prob. 109RECh. 5 - Area with a parameter Let a 0 be a real number...Ch. 5 - Inverse tangent integral Prove that for nonzero...Ch. 5 - Prob. 112RECh. 5 - Prob. 113RECh. 5 - Exponential inequalities Sketch a graph of f(t) =...Ch. 5 - Equivalent equations Explain why if a function u...Ch. 5 - Unit area sine curve Find the value of c such that...Ch. 5 - Unit area cubic Find the value of c0 such that the...
Additional Math Textbook Solutions
Find more solutions based on key concepts
In Exercises 1–4, use the grid and a straight edge to make a rough estimate of the slope of the curve (in y-uni...
University Calculus: Early Transcendentals (4th Edition)
Two fair dice are rolled. What is the conditional probability that at least one lands on 6 given that the dice ...
A First Course in Probability (10th Edition)
Women’s Heights Assume that college women’s heights are approximately Normally distributed with a mean of 65 in...
Introductory Statistics
To add polynomial
Pre-Algebra Student Edition
In hypothesis testing, the common level of significance is =0.05. Some might argue for a level of significance ...
Basic Business Statistics, Student Value Edition
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- A cable television company estimates that with x thousand subscribers, its monthly revenue and cost (in thousands of dollars) are given by the following equations. R(x) = 45x - 0.24x2 C(x) = 257 + 13xarrow_forwardx³-343 If k(x) = x-7 complete the table and use the results to find lim k(x). X-7 x 6.9 6.99 6.999 7.001 7.01 7.1 k(x) Complete the table. X 6.9 6.99 6.999 7.001 7.01 7.1 k(x) (Round to three decimal places as needed.)arrow_forward(3) (4 points) Given three vectors a, b, and c, suppose: |bx c = 2 |a|=√√8 • The angle between a and b xc is 0 = 135º. . Calculate the volume a (bxc) of the parallelepiped spanned by the three vectors.arrow_forward
- Calculate these limits. If the limit is ∞ or -∞, write infinity or-infinity. If the limit does not exist, write DNE: Hint: Remember the first thing you check when you are looking at a limit of a quotient is the limit value of the denominator. 1. If the denominator does not go to 0, you should be able to right down the answer immediately. 2. If the denominator goes to 0, but the numerator does not, you will have to check the sign (±) of the quotient, from both sides if the limit is not one-sided. 3. If both the numerator and the denominator go to 0, you have to do the algebraic trick of rationalizing. So, group your limits into these three forms and work with them one group at a time. (a) lim t-pi/2 sint-√ sin 2t+14cos ² t 7 2 2 2cos t (b) lim sint + sin 2t+14cos = ∞ t-pi/2 2 2cos t (c) lim cost-√sin 2t+14cos² t = t-pi/2 2cos t (d) lim t→pi/2 cost+√ sin t + 14cos 2cos ² t = ∞ (e) lim sint-v sin 2 t + 14cos = 0 t-pi/2 (f) lim t-pi/2 sin t +√ sin 2sin 2 t 2 t + 14cos t 2sin t cost- (g)…arrow_forwardThink of this sheet of paper as the plane containing the vectors a = (1,1,0) and b = (2,0,0). Sketch the parallelogram P spanned by a and b. Which diagonal of P represents the vector a--b geometrically?arrow_forward(1) (14 points) Let a = (-2, 10, -4) and b = (3, 1, 1). (a) (4 points) Using the dot product determine the angle between a and b. (b) (2 points) Determine the cross product vector axb. (c) (4 points) Calculate the area of the parallelogram spanned by a and b. Justify your answer. 1arrow_forward
- (d) (4 points) Think of this sheet of paper as the plane containing the vectors a = (1,1,0) and b = (2,0,0). Sketch the parallelogram P spanned by a and b. Which diagonal of P represents the vector ab geometrically? d be .dx adjarrow_forward(2) (4 points) Find all vectors v having length 1 that are perpendicular to both =(2,0,2) and j = (0,1,0). Show all work. a=arrow_forwardFor the following function, find the full power series centered at a of convergence. 0 and then give the first 5 nonzero terms of the power series and the open interval = f(2) Σ 8 1(x)--(-1)*(3)* n=0 ₤(x) = + + + ++... The open interval of convergence is: 1 1 3 f(x)= = 28 3x6 +1 (Give your answer in help (intervals) .)arrow_forward
- For the following function, find the full power series centered at x = 0 and then give the first 5 nonzero terms of the power series and the open interval of convergence. f(x) = Σ| n=0 9 f(x) = 6 + 4x f(x)− + + + ++··· The open interval of convergence is: ☐ (Give your answer in help (intervals) .)arrow_forwardLet X be a random variable with the standard normal distribution, i.e.,X has the probability density functionfX(x) = 1/√2π e^-(x^2/2)2 .Consider the random variablesXn = 20(3 + X6) ^1/2n e ^x^2/n+19 , x ∈ R, n ∈ N.Using the dominated convergence theorem, prove that the limit exists and find it limn→∞E(Xn)arrow_forwardLet X be a discrete random variable taking values in {0, 1, 2, . . . }with the probability generating function G(s) = E(sX). Prove thatVar(X) = G′′(1) + G′(1) − [G′(1)]2.[5 Marks](ii) Let X be a random variable taking values in [0,∞) with proba-bility density functionfX(u) = (5/4(1 − u^4, 0 ≤ u ≤ 1,0, otherwise. Let y =x^1/2 find the probability density function of Yarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Definite Integral Calculus Examples, Integration - Basic Introduction, Practice Problems; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=rCWOdfQ3cwQ;License: Standard YouTube License, CC-BY