Essential Calculus: Early Transcendentals
2nd Edition
ISBN: 9781133112280
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 5.1, Problem 2E
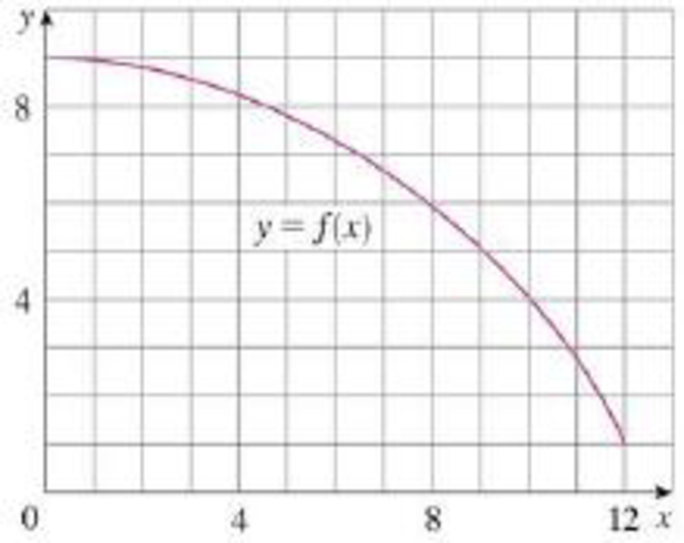
(a) Use six rectangles to find estimates of each type for the area under the given graph of f from x = 0 to x = 12.
(i) L6 (sample points are left endpoints)
(ii) R6 (sample points are right endpoints)
(iii) M6 (sample points are midpoints)
(b) Is L6 an underestimate or overestimate of the true area?
(c) Is R6 an underestimate or overestimate of the true area?
(d) Which of the numbers L6, R6, or M6 gives the best estimate? Explain.
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
(a) Use six rectanges to find estimates of each type for the area under the given graph of f from x = 0 to x = 12.
(i) L6 (sample points are left endpoints)
(ii) R6 (sample points are right endpoints)
(iii) M6 (sample points are midpoints)
(b) Is L6 an underestimate or overestimate of the true area?
(c) Is R6 an underestimate or overestimate of the true area?
(d) Which of the numbers L6 , R6 , or M6 gives the best estimate? Explain.
*please use handwriting not typing, i understand it better that way. thank you*
Consider the following.
y
16
| y = f(x)
16
(a) Use six rectangles to find estimates of each type for the area under the given graph of f from x = 0 to x = 24.
(i) Sample points are left endpoints.
(ii) Sample points are right endpoints.
(iii) Sample points are midpoints.
M6
%3D
(a) By reading values from the given graph of f, use five rectangles to find a lower estimate and an upper estimate for the area under the given graph of f from
x = 0 to x = 10.
Lower estimate 2
Upper estimate a
(b) Repeat part (a) with 10 rectangles in each case.
Lower estimate 2
Upper estimate 2
Chapter 5 Solutions
Essential Calculus: Early Transcendentals
Ch. 5.1 - Prob. 1ECh. 5.1 - (a) Use six rectangles to find estimates of each...Ch. 5.1 - (a) Estimate the area under the graph of f(x)=x...Ch. 5.1 - Prob. 3ECh. 5.1 - (a) Estimate the area under the graph of f(x) = 1...Ch. 5.1 - Prob. 6ECh. 5.1 - Prob. 7ECh. 5.1 - Prob. 8ECh. 5.1 - The speed of a runner increased steadily during...Ch. 5.1 - Speedometer readings for a motorcycle at 12-second...
Ch. 5.1 - Prob. 11ECh. 5.1 - Prob. 12ECh. 5.1 - The velocity graph of a braking car is shown. Use...Ch. 5.1 - Prob. 14ECh. 5.1 - Use Definition 2 to find an expression for the...Ch. 5.1 - Prob. 16ECh. 5.1 - Prob. 17ECh. 5.1 - Prob. 18ECh. 5.1 - Prob. 19ECh. 5.1 - Prob. 20ECh. 5.1 - (a) Let An be the area of a polygon with n equal...Ch. 5.2 - Evaluate the Riemann sum for f(x)=312x,2x14, with...Ch. 5.2 - Prob. 2ECh. 5.2 - If f(x)=ex2, 0 x 2, find the Riemann sum with n...Ch. 5.2 - Prob. 4ECh. 5.2 - Prob. 5ECh. 5.2 - Find the Riemann sum for f (x) = x + x2, 2x0, if...Ch. 5.2 - Prob. 7ECh. 5.2 - Prob. 8ECh. 5.2 - Prob. 9ECh. 5.2 - Prob. 10ECh. 5.2 - Prob. 11ECh. 5.2 - Prob. 12ECh. 5.2 - Prob. 13ECh. 5.2 - Prob. 14ECh. 5.2 - Express the limit as a definite integral on the...Ch. 5.2 - Prob. 16ECh. 5.2 - Prob. 17ECh. 5.2 - Prob. 18ECh. 5.2 - Prob. 19ECh. 5.2 - Use the form of the definition of the integral...Ch. 5.2 - Prob. 21ECh. 5.2 - Prob. 22ECh. 5.2 - Prob. 23ECh. 5.2 - Prob. 24ECh. 5.2 - Prob. 25ECh. 5.2 - 25–26 Express the integral as a limit of Riemann...Ch. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Prob. 31ECh. 5.2 - Prob. 32ECh. 5.2 - Evaluate the integral by interpreting it in terms...Ch. 5.2 - Evaluate the integral by interpreting it in terms...Ch. 5.2 - 31–36 Evaluate the integral by interpreting it in...Ch. 5.2 - 3136 Evaluate the integral by interpreting it in...Ch. 5.2 - Evaluate sin2xcos4xdx.Ch. 5.2 - Given that 013xx2+4dx=558, what is 103uu2+4du?Ch. 5.2 - Write as a single integral in the form abf(x)dx:...Ch. 5.2 - If 15f(x)dx=12 and 45f(x)dx=3.6, find 14f(x)dx.Ch. 5.2 - If 09f(x)dx=37 and 09g(x)dx=16, find...Ch. 5.2 - Find 05f(x)dx if f(x)={3forx3xforx3Ch. 5.2 - In Example 2 in Section 5.1 we showed that...Ch. 5.2 - If , F(x)=2xf(t)dt, where f is the function whose...Ch. 5.2 - Prob. 45ECh. 5.2 - Prob. 46ECh. 5.2 - Prob. 47ECh. 5.2 - Use Property 8 to estimate the value of the...Ch. 5.2 - Use Property 8 to estimate the value of the...Ch. 5.2 - 61. Use Property 8 to estimate the value of the...Ch. 5.2 - Use Property 8 to estimate the value of the...Ch. 5.2 - Use Property 8 to estimate the value of the...Ch. 5.2 - Express the limit as a definite integral....Ch. 5.3 - 32. Evaluate the integral.
Ch. 5.3 - Evaluate the integral. 01coshtdtCh. 5.3 - Prob. 22ECh. 5.3 - Prob. 23ECh. 5.3 - Prob. 24ECh. 5.3 - Prob. 25ECh. 5.3 - Prob. 35ECh. 5.3 - Prob. 36ECh. 5.3 - Prob. 37ECh. 5.3 - Prob. 38ECh. 5.3 - Prob. 31ECh. 5.3 - Prob. 33ECh. 5.3 - Prob. 34ECh. 5.3 - Prob. 39ECh. 5.3 - Prob. 40ECh. 5.3 - Prob. 69ECh. 5.3 - Prob. 32ECh. 5.3 - Prob. 70ECh. 5.3 - Prob. 45ECh. 5.3 - Find the general indefinite integral. (x3+x23)dxCh. 5.3 - Prob. 46ECh. 5.3 - Prob. 47ECh. 5.3 - Prob. 43ECh. 5.3 - Prob. 48ECh. 5.3 - Prob. 41ECh. 5.3 - Prob. 42ECh. 5.3 - Prob. 1ECh. 5.3 - Prob. 2ECh. 5.3 - Prob. 3ECh. 5.3 - Prob. 4ECh. 5.3 - Prob. 5ECh. 5.3 - Prob. 6ECh. 5.3 - Prob. 7ECh. 5.3 - Prob. 8ECh. 5.3 - Prob. 9ECh. 5.3 - Prob. 10ECh. 5.3 - Prob. 11ECh. 5.3 - Evaluate the integral. 14yyy2dyCh. 5.3 - Prob. 13ECh. 5.3 - Prob. 14ECh. 5.3 - Prob. 15ECh. 5.3 - Prob. 17ECh. 5.3 - Prob. 18ECh. 5.3 - Prob. 20ECh. 5.3 - Prob. 21ECh. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - Prob. 28ECh. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - Prob. 49ECh. 5.3 - Prob. 50ECh. 5.3 - Prob. 51ECh. 5.3 - Prob. 52ECh. 5.3 - Prob. 53ECh. 5.3 - Prob. 54ECh. 5.3 - Prob. 55ECh. 5.3 - Prob. 56ECh. 5.3 - Prob. 57ECh. 5.3 - Prob. 58ECh. 5.3 - Prob. 59ECh. 5.3 - 5960 The velocity function (in meters per second)...Ch. 5.3 - Prob. 61ECh. 5.3 - Prob. 62ECh. 5.3 - Prob. 65ECh. 5.3 - Prob. 63ECh. 5.3 - Prob. 64ECh. 5.3 - Prob. 66ECh. 5.3 - Prob. 67ECh. 5.3 - Prob. 68ECh. 5.4 - Let g(x)=0xf(t)dt, where f is the function whose...Ch. 5.4 - Let g(x)=0xf(t)dt, where f is the function whose...Ch. 5.4 - Sketch the area represented by g(x). Then find...Ch. 5.4 - Prob. 4ECh. 5.4 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.4 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.4 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.4 - 514 Use Part 1 of the Fundamental Theorem of...Ch. 5.4 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.4 - 514 Use Part 1 of the Fundamental Theorem of...Ch. 5.4 - 514 Use Part 1 of the Fundamental Theorem of...Ch. 5.4 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.4 - Find the derivative of the function....Ch. 5.4 - 514 Use Part 1 of the Fundamental Theorem of...Ch. 5.4 - On what interval is the curve y=0xt2t2+t+2dt...Ch. 5.4 - Prob. 24ECh. 5.4 - Prob. 27ECh. 5.4 - Prob. 28ECh. 5.4 - Prob. 25ECh. 5.4 - Prob. 26ECh. 5.4 - Find a function f and a number a such that...Ch. 5.4 - A manufacturing company owns a major piece of...Ch. 5.4 - A high-tech company purchases a new computing...Ch. 5.4 - Find the average value of the function on the...Ch. 5.4 - 15-18 Find the average value of the function on...Ch. 5.4 - Find the average value of the function on the...Ch. 5.4 - Find the average value of the function on the...Ch. 5.4 - Prob. 19ECh. 5.4 - Prob. 20ECh. 5.4 - Prob. 21ECh. 5.4 - Prob. 22ECh. 5.5 - Evaluate the integral by making the given...Ch. 5.5 - Prob. 2ECh. 5.5 - Prob. 3ECh. 5.5 - Prob. 4ECh. 5.5 - Prob. 5ECh. 5.5 - Prob. 6ECh. 5.5 - Prob. 7ECh. 5.5 - Evaluate the indefinite integral. x2ex3dxCh. 5.5 - Prob. 9ECh. 5.5 - Prob. 10ECh. 5.5 - Evaluate the indefinite integral. (lnx)2xdxCh. 5.5 - Prob. 12ECh. 5.5 - Prob. 13ECh. 5.5 - Prob. 14ECh. 5.5 - Prob. 20ECh. 5.5 - Prob. 16ECh. 5.5 - Prob. 17ECh. 5.5 - Prob. 18ECh. 5.5 - Prob. 15ECh. 5.5 - Prob. 25ECh. 5.5 - Evaluate the indefinite integral. sinh2xcoshxdxCh. 5.5 - Evaluate the indefinite integral. sin(lnx)xdxCh. 5.5 - Prob. 23ECh. 5.5 - Prob. 24ECh. 5.5 - Prob. 19ECh. 5.5 - Prob. 26ECh. 5.5 - Prob. 27ECh. 5.5 - Prob. 28ECh. 5.5 - Prob. 29ECh. 5.5 - Prob. 30ECh. 5.5 - Prob. 31ECh. 5.5 - Prob. 32ECh. 5.5 - Prob. 36ECh. 5.5 - Evaluate the indefinite integral. 1+x1+x2dxCh. 5.5 - Prob. 33ECh. 5.5 - Prob. 34ECh. 5.5 - Prob. 37ECh. 5.5 - Prob. 38ECh. 5.5 - Evaluate the definite integral. 011+7x3dxCh. 5.5 - Evaluate the definite integral. 03dx5x+1Ch. 5.5 - Prob. 41ECh. 5.5 - Prob. 42ECh. 5.5 - Prob. 43ECh. 5.5 - Prob. 44ECh. 5.5 - Prob. 50ECh. 5.5 - Prob. 45ECh. 5.5 - Prob. 48ECh. 5.5 - Evaluate the definite integral. ee4dxxlnxCh. 5.5 - Prob. 49ECh. 5.5 - Prob. 47ECh. 5.5 - Evaluate the indefinite integral. /2/2x2sinx1+x6dxCh. 5.5 - Prob. 52ECh. 5.5 - Prob. 57ECh. 5.5 - 78. Evaluate by making a substitution and...Ch. 5.5 - Prob. 59ECh. 5.5 - Prob. 60ECh. 5.5 - Prob. 61ECh. 5.5 - Prob. 62ECh. 5.5 - Prob. 63ECh. 5.5 - Prob. 64ECh. 5.5 - Prob. 65ECh. 5.5 - Prob. 66ECh. 5.5 - 89. If f is continuous on , prove that
For the...Ch. 5.5 - Prob. 68ECh. 5.5 - Prob. 69ECh. 5.5 - Find the average value of the function on the...Ch. 5.5 - Prob. 54ECh. 5.5 - Prob. 56ECh. 5.5 - Find the average value of the function on the...Ch. 5 - Prob. 1RCCCh. 5 - Prob. 2RCCCh. 5 - Prob. 3RCCCh. 5 - Prob. 6RCCCh. 5 - Prob. 4RCCCh. 5 - Prob. 7RCCCh. 5 - Prob. 5RCCCh. 5 - Prob. 9RCCCh. 5 - Prob. 10RCCCh. 5 - Prob. 1RQCh. 5 - Prob. 2RQCh. 5 - Prob. 3RQCh. 5 - Prob. 4RQCh. 5 - Prob. 5RQCh. 5 - Prob. 6RQCh. 5 - Prob. 7RQCh. 5 - Prob. 8RQCh. 5 - Determine whether the statement is true or false....Ch. 5 - Prob. 10RQCh. 5 - Prob. 11RQCh. 5 - Prob. 12RQCh. 5 - Prob. 13RQCh. 5 - 14. Determine whether the statement is true or...Ch. 5 - Prob. 15RQCh. 5 - Prob. 16RQCh. 5 - Determine whether the statement is true or false....Ch. 5 - Prob. 18RQCh. 5 - Prob. 1RECh. 5 - Prob. 2RECh. 5 - Prob. 3RECh. 5 - Prob. 4RECh. 5 - Prob. 5RECh. 5 - Prob. 6RECh. 5 - Prob. 7RECh. 5 - Prob. 8RECh. 5 - Evaluate the integral, if it exists. 01(1x9)dxCh. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Prob. 12RECh. 5 - Prob. 13RECh. 5 - Prob. 14RECh. 5 - Prob. 16RECh. 5 - Prob. 15RECh. 5 - Prob. 18RECh. 5 - Evaluate the integral, if it exists....Ch. 5 - Prob. 20RECh. 5 - Prob. 19RECh. 5 - Prob. 21RECh. 5 - Prob. 22RECh. 5 - Prob. 23RECh. 5 - Prob. 24RECh. 5 - Prob. 25RECh. 5 - Evaluate the integral, if it exists. cos(lnx)xdxCh. 5 - Prob. 27RECh. 5 - Prob. 28RECh. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - Prob. 33RECh. 5 - Prob. 34RECh. 5 - Prob. 35RECh. 5 - Prob. 36RECh. 5 - Prob. 37RECh. 5 - Prob. 38RECh. 5 - Prob. 39RECh. 5 - Prob. 40RECh. 5 - Prob. 41RECh. 5 - A particle moves along a line with velocity...Ch. 5 - Prob. 43RECh. 5 - Prob. 44RECh. 5 - Prob. 45RECh. 5 - Prob. 48RECh. 5 - Prob. 49RECh. 5 - Prob. 50RECh. 5 - Prob. 8RCCCh. 5 - Prob. 46RECh. 5 - If f is a continuous function, what is the limit...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Can the average rate of change of a function be constant?arrow_forwardFind two z values so that 37% of the middle area is bounded by themarrow_forwardThe graph of the function f is given. y y = f(x) 4 2 X 0 2 4 6 8 10 12 (a) Use six rectangles to find estimates of each type for the area under the given graph of f, the x-axis, and the lines x = 0 and x = 12. (i) L (sample points are left endpoints) = 46 (ii) R (sample points are right endpoints) R6 = (iii) M6 (sample points are midpoints) M6 = (b) Is L an underestimate or overestimate of the true area? 6 overestimate underestimate (c) Is R6 an underestimate or overestimate of the true area? overestimate underestimate (d) Which of the numbers! D or M O O 8 6 OO gives the best estimate of the true area?arrow_forward
- Consider the following. y 8 y = f(x) 4 8 (a) Use six rectangles to find estimates of each type for the area under the given graph of f from x = 0 to x = 12. (i) Sample points are left endpoints. L6 = (ii) Sample points are right endpoints. R5 = (iii) Sample points are midpoints. M5 = (b) Is Lg an underestimate or overestimate of the true area? O overestimate O underestimate (c) Is Rg an underestimate or overestimate of the true area? O overestimate O underestimate (d) Which of the numbers gives the best estimate? O L6 O M6 O R5arrow_forwardEconomists use Lorenz curves to illustrate the distribution of income in a country. A Lorenz curve, y = f(x), represents the actual income distribution in the country. In this model, x represents percents of families in the country from the poorest to the wealthiest and y represents percents of total income. The model y = x represents a country in which each family has the same income. The area between these two models, where 0 ≤ x ≤ 100, indicates a country’s “income inequality.” The table lists percents of income y for selected percents of families x in a country. (a) Use a graphing utility to find a quadratic model for the Lorenz curve. (b) Plot the data and graph the model. (c) Graph the model y = x. How does this model compare with the model in part (a)? (d) Use the integration capabilities of a graphing utility to approximate the “income inequality.”arrow_forward8 Can you help me with thisarrow_forward
- The scatter plot displays bivarlate data on the outside temperature in degrees Fahrenheit, x, and the corresponding number of beachgoers, y, at a local beach. Temperature and Beachgoers 60 50 30 20 10 55 60 65 70 75 Temperature ("F) 85 Outliers appear to be located at (66, 45) and (85, 15). | The outlier (66, 45) represents 45 beachgoers visiting the beach on a day when the outside temperature was 65°F. The outlier (85, 15) represents 15 beachgoers at the beach on a day when the outside temperature was 85°F. Perhaps on the 85° day, people attended a big event, such as a football game instead of the beach. This could explain why fewer people attended the beach. Likewise, maybe there was a special competition at the beach on the day that the temperature was 66°F. This could explain why more people went to the beach even though it was not very warm. The strong, positive, and linear association indicates that there are more beachgoers on warmer days. The general trend shows that, for…arrow_forwardAn individual’s income varies with his or her age. The following table shows the median income I of males of different age groups within the United States for 2012. For each age group, let the class midpoint represent theindependent variable, x. For the class “65 years and older,” we will assume that the class midpoint is 69.5. (a) Use a graphing utility to draw a scatter diagram of thedata. Comment on the type of relation that may existbetween the two variables.(b) Use a graphing utility to find the quadratic function ofbest fit that models the relation between age and medianincome.(c) Use the function found in part (b) to determine the age atwhich an individual can expect to earn the most income.(d) Use the function found in part (b) to predict the peakincome earned.(e) With a graphing utility, graph the quadratic function ofbest fit on the scatter diagram.arrow_forwardWhat is the type of the variable "The average speed of busses traveling through a major crossroad between 7:30 am and 8:30 am on a Sunday"? O a. Qualitative - Ordinal O b. Quantitative - Discrete O c. Qualitative - Nominal O d. Quantitative - Continuousarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Area Between The Curve Problem No 1 - Applications Of Definite Integration - Diploma Maths II; Author: Ekeeda;https://www.youtube.com/watch?v=q3ZU0GnGaxA;License: Standard YouTube License, CC-BY