
Concept explainers
The range of the values of the mass m2 so that the two connected blocks resting on two inclined planes are in equilibrium.
Answer to Problem 83QAP
The mass m2 can have values between 3.51 kg and 52.64 kg for the system of masses to be in equilibrium.
Explanation of Solution
Given info:
Formula used:
From the diagram given, if the value of m2 falls below a certain value, it would slide up the plane and the block of mass m1 would slide down. This gives the value of the minimum mass of m2.
If the value of m2 increases beyond a certain value, the block would slide down the plane and the block of mass m1 would slide up.
By drawing the free body diagrams for each case, and applying the force equations for each case, the range of the values of m2 can be determined.
Explanation and Calculation:
Case 1:
Consider the case when the block 1slides down the plane and the block 2 slides up the plane.
The free body diagram for m1 is shown below:
The block rests on an incline which makes an angle
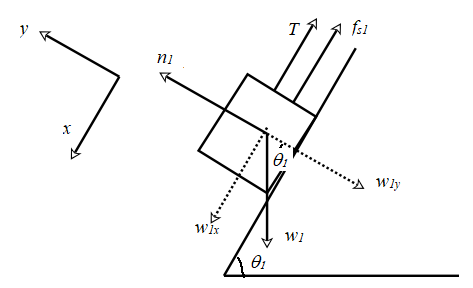
The weight
Resolve the weight w1 into components along the +x and −y directions as shown. The magnitudes of the components are given by,
Write the force equation along the +y direction.
Since the block is in equilibrium,
Therefore,
The force of friction is given by,
The system is in equilibrium along the x direction too. Therefore,
Using equations (1) and (2), in the above equation,
In a similar manner, construct a free body diagram for the block 2.
The block rests on an incline which makes an angle
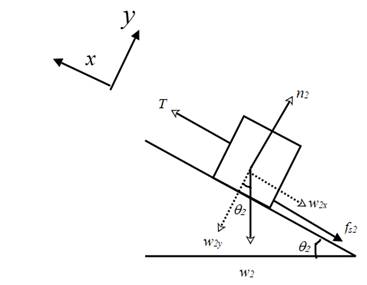
The weight
Resolve the weight w2 into components along the −x and −y directions as shown. The magnitudes of the components are given by,
Write the force equation along the +y direction and apply the condition for equilibrium.
Therefore,
The force of friction is given by,
The system is in equilibrium along the x direction too. Therefore,
Using equations (4) and (6), in the above equation,
Add equations (3) and (7) and write an expression for m2.
Substitute the known values of the variables in the expression and calculate the value of m2.
The minimum value of m2 for which the system is in equilibrium is 3.51 kg.
Case 2:
Consider the case when the block 1slides up the plane and the block 2 slides down the plane.
The free body diagram for m1 is shown below:
Assume the +x direction up the incline and the +y direction perpendicular to the plane. The weight
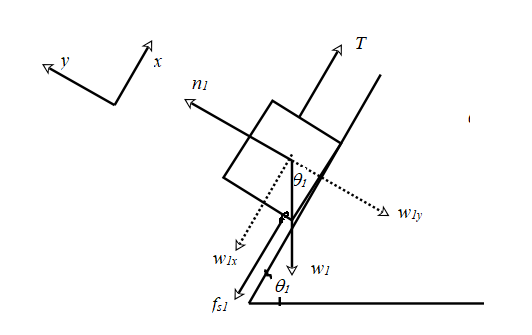
The equations (1) and (2) are applied to this free body diagram too.
Write the condition for equilibrium along the x direction.
Use equations (1) and (2) in the expression.
In a similar manner, construct a free body diagram for the block 2.
. Assume a coordinate system which has the +x direction pointing down the plane and the +y direction perpendicular to the plane away from it. The weight
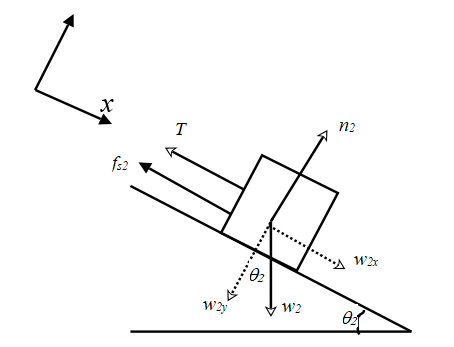
The equations (4), (5) and (6) are valid for this case too.
Write the equation for equilibrium along the x direction.
Using equations (4) and (6) in the expression,
Add equations (8) and (9) and write an expression for m2.
Substitute the known values of the variables in the expression.
The maximum value of m2 for the system to be in equilibrium is 52.64 kg.
Conclusion:
Thus, the mass m2 can have values between 3.51 kg and 52.64 kg for the system of masses to be in equilibrium.
Want to see more full solutions like this?
Chapter 5 Solutions
FlipIt for College Physics (Algebra Version - Six Months Access)
- Calculate the value of the force F at which the 20 kg uniformly dense cabinet will start to tip. Calculate the acceleration of the cabinet at this force F. Must include the FBD and KD of the system. Ignore friction.arrow_forward1) A 2.0 kg toy car travelling along a smooth horizontal surface experiences a horizontal force Fas shown in the picture to the left. Assuming the rightward direction to be positive and if the car has an initial velocity of 60.0m/s to the right, calculate the velocity of the car after the first 10.0s of motion. (Force is in Newtons and time in seconds). (Hint: Use impulse-momentum theorem) F 5.0 10 0 -10arrow_forward3) Two bumper cars of masses 600 kg and 900 kg travelling (on a smooth surface) with velocities 8m/s and 4 m/s respectively, have a head on collision. If the coefficient of restitution is 0.5. a) What sort of collision is this? b) Calculate their velocities immediately after collision. c) If the coefficient of restitution was 1 instead of 0.5, what is the amount of energy lost during collision?arrow_forward
- The rectangular loop of wire shown in the figure (Figure 1) has a mass of 0.18 g per centimeter of length and is pivoted about side ab on a frictionless axis. The current in the wire is 8.5 A in the direction shown. Find the magnitude of the magnetic field parallel to the y-axis that will cause the loop to swing up until its plane makes an angle of 30.0 ∘ with the yz-plane. Find the direction of the magnetic field parallel to the y-axis that will cause the loop to swing up until its plane makes an angle of 30.0 ∘ with the yz-plane.arrow_forwardGive a more general expression for the magnitude of the torque τ. Rewrite the answer found in Part A in terms of the magnitude of the magnetic dipole moment of the current loop m. Define the angle between the vector perpendicular to the plane of the coil and the magnetic field to be ϕ, noting that this angle is the complement of angle θ in Part A. Give your answer in terms of the magnetic moment mm, magnetic field B, and ϕ.arrow_forwardCalculate the electric and magnetic energy densities at thesurface of a 3-mm diameter copper wire carrying a 15-A current. The resistivity ofcopper is 1.68×10-8 Ω.m.Prob. 18, page 806, Ans: uE= 5.6 10-15 J/m3 uB= 1.6 J/m3arrow_forward
- A 15.8-mW laser puts out a narrow beam 2.0 mm in diameter.Suppose that the beam is in free space. What is the rms value of E in the beam? What isthe rms value of B in the beam?Prob. 28, page 834. Ans: Erms= 1380 V/m, Brms =4.59×10-6 Tarrow_forwardA 4.5 cm tall object is placed 26 cm in front of a sphericalmirror. It is desired to produce a virtual image that is upright and 3.5 cm tall.(a) What type of mirror should be used, convex, or concave?(b) Where is the image located?(c) What is the focal length of the mirror?(d) What is the radius of curvature of the mirror?Prob. 25, page 861. Ans: (a) convex, (b) di= -20.2 cm, i.e. 20.2 cm behind the mirror,(c) f= -90.55 cm, (d) r= -181.1 cm.arrow_forwardA series RCL circuit contains an inductor with inductance L=3.32 mH, and a generator whose rms voltage is 11.2 V. At a resonant frequencyof 1.25 kHz the average power delivered to the circuit is 26.9 W.(a) Find the value of the capacitance.(b) Find the value of the resistance.(c) What is the power factor of this circuit?Ans: C=4.89 μF, R=4.66 Ω, 1.arrow_forward
- A group of particles is traveling in a magnetic field of unknown magnitude and direction. You observe that a proton moving at 1.70 km/s in the +x-direction experiences a force of 2.06×10−16 N in the +y-direction, and an electron moving at 4.40 km/s in the −z-direction experiences a force of 8.10×10−16 N in the +y-direction. What is the magnitude of the magnetic force on an electron moving in the −y-direction at 3.70 km/s ? What is the direction of this the magnetic force? (in the xz-plane)arrow_forwardA particle with a charge of −5.20 nC is moving in a uniform magnetic field of B =−( 1.22 T )k^. The magnetic force on the particle is measured to be F=−( 3.50×10−7 N )i^+( 7.60×10−7 N )j^. Calculate the x component of the velocity of the particle.arrow_forwardIs it possible for average velocity to be negative?a. Yes, in cases when the net displacement is negative.b. Yes, if the body keeps changing its direction during motion.c. No, average velocity describes only magnitude and not the direction of motion.d. No, average velocity describes only the magnitude in the positive direction of motion.arrow_forward
 Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





