Chapter 5, Problem 79QAP

To determine

The magnitude of the tension in the string which connects two blocks, one of which hangs vertically down and the other resting on an inclined plane.

Answer to Problem 79QAP

The tension in the string is found to be 3.92 N.

Explanation of Solution

Given info:

Mass of the block placed on the incline

  $m_1=1.00\text{ kg}$

Mass of the hanging block

  $m_2=0.400\text{ kg}$

Angle made by the plane with horizontal

  $\theta =30.0°$

Coefficient of static friction

  ${\mu }_s=0.500$

Coefficient of kinetic friction

  ${\mu }_k=0.400$

Formula used:

Free body diagrams are drawn for the two blocks and the tension in the string is determined using the force equations for both the blocks.

The free body diagram for the block of mass $m_2$, assuming the positive x axis pointing upwards and the y axis perpendicular to it is shown below.

The weight of the block is ${\overrightarrow{w}}_2$, which acts along the −x direction and the tension $\overrightarrow{T}$ acts along the +x direction.

  

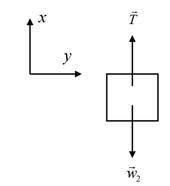
The total force acting along the +x direction is given by,

  ${\displaystyle \sum F_{2x}}=T-w_2$......(1)

Draw the free body diagram for the block of mass $m_1$ assuming that the block tends to slide down the plane. This would result in the force of friction $\overrightarrow{f}$ to act upwards. The coordinate system under consideration has its +x direction pointing down along the incline and the +y direction perpendicular to the incline.

  

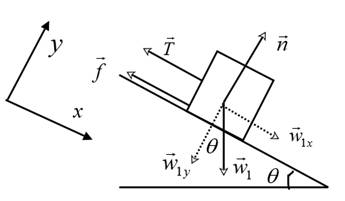
The weight ${\overrightarrow{w}}_1$ acts downwards and the normal force $\overrightarrow{n}$ acts along the +y direction. The force of friction $\overrightarrow{f}$ and the tension $\overrightarrow{T}$ acts parallel to the plane along the −x direction.

Resolve the weight ${\overrightarrow{w}}_1$ into two components ${\overrightarrow{w}}_{1x}$ and ${\overrightarrow{w}}_{1y}$ along the +x and the +y directions.

The force equation along the +x direction is given by,

  ${\displaystyle \sum F_{1x}}=w_{1x}-f-T$......(2)

The force equation along the +y direction is given by,

  ${\displaystyle \sum F_{1y}}=n-w_{1y}$......(3)

Since the block is in equilibrium in the y direction,

  ${\displaystyle \sum F_{1y}}=n-w_{1y}=0$

Hence,

  $n=w_{1y}$......(4)

The force of friction and the normal force are related as follows:

  $f=\mu n$......(5)

The value of the coefficient of friction $\mu$ takes the value of ${\mu }_s$ if the block is at rest and ${\mu }_k$ if the block is in motion.

Calculation:

The system would be at rest, if the following conditions are satisfied:

  ${\displaystyle \sum F_{2x}}=0$

and ${\displaystyle \sum F_{1x}}=0$

If ${\displaystyle \sum F_{2x}}=0$, then from equation (1),

  $T=w_2$

Since $w_2=m_{2}g$, where g is the acceleration of free fall

  $T=m_{2}g$

Substitute the values of the variables in the above equation,

  $\begin{array}{c}T=m_{2}g\\ =\left(0.400\text{ kg}\right)\left(9.80{\text{ m/s}}^2\right)\\ =3.92\text{ N}\end{array}$

To check whether the system is at rest, use the expression ${\displaystyle \sum F_{1x}}=0$.

Therefore,

  $w_{1x}-f-T=0$

Calculate the value of $w_{1x}-T$.

The component $w_{1x}=w_1\sin \theta$, where, $w_1=m_{1}g$.

Therefore,

  $w_{1x}-T=m_{1}g\sin \theta -T$

Use the values of the variables in the equation.

  $\begin{array}{c}{w}_{1x}-T=m_{1}g\sin \theta -T\\ =\left(1.00\text{ kg}\right)\left(9.80{\text{ m/s}}^2\right)\left(\sin 30.0°\right)-3.92\text{ N}\\ =4.90\text{ N}-3.92\text{ N}\\ =0.98\text{ N}\end{array}$

If the system is at rest, assume the maximum force of static friction to act on the block.

Then,

  $f_{\max }={\mu }_{s}n$

From equation (4),

  $\begin{array}{c}{f}_{\max }={\mu }_{s}n\\ ={\mu }_s{w}_{1y}\end{array}$

The component $w_{1y}$ is given by,

  $w_{1y}=w_1\cos \theta$, where $w_1=m_{1}g$

Calculate the maximum force of static friction acting on the block.

  $\begin{array}{c}{f}_{\max }={\mu }_s{w}_{1y}\\ ={\mu }_s{m}_{1}g\cos \theta \\ =\left(0.500\right)\left(1.00\text{ kg}\right)\left(9.80{\text{ m/s}}^2\right)\left(\cos 30.0°\right)\\ =4.24\text{ N}\end{array}$

It can be seen that $f_{\max }>w_{1x}-T$, which proves that the block on the incline is at rest.

Conclusion:

Since the system is at rest, the force of tension in the string is equal to 3.92 N.