
Concept explainers
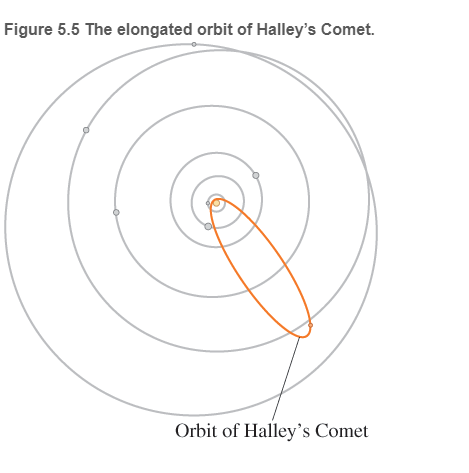
Halley's Comet Edmond Halley was the first to realize that the comets observed in 1531,1607, and 1682 were really one comet (now called Halley's Comet) that moved around the Sun in an elongated elliptical orbit (see Figure 5.5). He predicted that the peanut-shaped comet would reappear in 1757. It appeared in March 1759 (attractions to Jupiter and Saturn delayed its trip by 618 days). More recent appearances of Halley’s Comet were in 1835, 1910, and 1986. It is expected again in 2061.
The nucleus of Halley's Comet is relatively small (15 km long. 8 km wide, and 8 km thick). It has a low
78 EST Use the velocity change method to estimate the comet's direction of acceleration when passing closest to the Sun (position I in Figure P5.78).
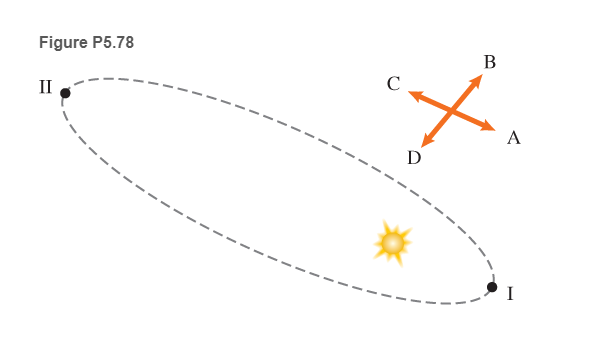
a. A b B
c. C
d. D
e. The acceleration is zero.
Want to see the full answer?
Check out a sample textbook solution
Chapter 5 Solutions
College Physics: Explore And Apply, Volume 2 (2nd Edition)
Additional Science Textbook Solutions
Organic Chemistry (8th Edition)
Concepts of Genetics (12th Edition)
Human Anatomy & Physiology (2nd Edition)
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
Campbell Biology (11th Edition)
Microbiology: An Introduction
- You have just bought a new bicycle. On your first riding trip, it seems that the bike comes to rest relatively quickly after you stop pedaling and let the bicycle coast on flat ground. You call the bicycle shop from which you purchased the vehicle and describe the problem. The technician says that they will replace the bearings in the wheels or do whatever else is necessary if you can prove that the frictional torque in the axle of the wheels is worse than -0.02 N . m. At first, you are discouraged by the technical sound of what you have been told and by the absence of any tool to measure torque in your garage. But then you remember that you are taking a physics class! You take your bike into the garage, turn it upside down and start spinning the wheel while you think about how to determine the frictional torque. The driveway outside the garage had a small puddle, so you notice that droplets of water are flying off the edge of one point on the tire tangentially, including drops that…arrow_forward2nd drop down is "up" or "down"arrow_forwardRomeo (79.0 kg) entertains Juliet (57.0 kg) by playing his guitar from the rear of their boat at rest in still water, 2.70 m away from Juliet, who is in the front of the boat. After the serenade, Juliet carefully moves to the rear of the boat (away from shore) to plant a kiss on Romeo's cheek. (a) How far (in m) does the 81.0 kg boat move toward the shore it is facing? m (b) What If? If the lovers both walk toward each other and meet at the center of the boat, how far (in m) and in what direction does the boat now move? magnitude m direction ---Select---arrow_forward
- 2nd image is the same for all drop downsarrow_forwardA mobile is constructed of light rods, light strings, and beach souvenirs as shown in the figure below. If m4 = 12.0 g, find values (in g) for the following. (Let d₁ = 3.20 cm, d₂ = 5.10 cm, d3 = 1.00 cm, d4 = 5.80 cm, d5 = 2.40 cm, and d6 = 3.20 cm.) d₁ d2 d3 d4 Mg d5 d6 mg MA mi (a) m₁ = g (b) m2 = (c) m3 = g g (d) What If? If m₁ accidentally falls off and shatters when it strikes the floor, the rod holding m will move to a vertical orientation so that m hangs directly below the end of the rod supporting m₂. To what values should m₂ equilibrium and be oriented horizontally? (Enter your answers in g.) m2 = m3 = and m3 be adjusted so that the other two rods will remain inarrow_forwardAn automobile tire is shown in the figure below. The tire is made of rubber with a uniform density of 1.10 × 103 kg/m³. The tire can be modeled as consisting of two flat sidewalls and a tread region. Each of the sidewalls has an inner radius of 16.5 cm and an outer radius of 30.5 cm as shown, and a uniform thickness of 0.600 cm. The tread region can be approximated as having a uniform thickness of 2.50 cm (that is, its inner radius is 30.5 cm and outer radius is 33.0 cm as shown) and a width of 19.2 cm. What is the moment of inertia (in kg . m²) of the tire about an axis perpendicular to the page through its center? 33.0 cm 30.5 cm kg. m² 16.5 cm Sidewall Treadarrow_forward
- John is pushing his daughter Rachel in a wheelbarrow when it is stopped by a brick 8.00 cm high (see the figure below). The handles make an angle of 0 = 17.5° with the ground. Due to the weight of Rachel and the wheelbarrow, a downward force of 403 N is exerted at the center of the wheel, which has a radius of 16.0 cm. Assume the brick remains fixed and does not slide along the ground. Also assume the force applied by John is directed exactly toward the center of the wheel. (Choose the positive x-axis to be pointing to the right.) i (a) What force (in N) must John apply along the handles to just start the wheel over the brick? N (b) What is the force (magnitude in kN and direction in degrees clockwise from the -x-axis) that the brick exerts on the wheel just as the wheel begins to lift over the brick? magnitude direction kN ° clockwise from the -x-axisarrow_forwardYour neighbor designs automobiles for a living. You are fascinated with her work. She is designing a new automobile and needs to determine how strong the front suspension should be. She knows of your fascination with her work and your expertise in physics, so she asks you to determine how large the normal force on the front wheels of her design automobile could become under a hard stop, when the wheels are locked and the automobile is skidding on the road. She gives you the following information. The mass of the automobile is m₂ = 1.10 × 103 kg and it can carry five passengers of average mass m = 80.0 kg. The front and rear wheels are separated by d = 4.45 m. The center of mass of the car carrying five passengers is dCM = 2.25 m behind the front wheels and hCM = 0.630 m above the roadway. A typical coefficient of kinetic friction between tires and roadway is μk = 0.840. (Caution: The braking automobile is not in an inertial reference frame. Enter the magnitude of the force in N.) Narrow_forwardThree solid, uniform boxes are aligned as in the figure below. Find the x- and y-coordinates (in m) of the center of mass of the three boxes, measured from the bottom left corner of box A. (Consider the three-box system.) HINT 0.200 m 0.280 m 0.120 m y A B C 0.350 m Origin 0.750 kg 1.00 kg 0.650 kg Х ст E m m Уст xarrow_forward
- Consider the truss shown in the figure, built from three struts attached by three pins. The truss supports a downward force of F = 1,080 N applied at the point B. Assume the mass of the truss is negligible, the pins are frictionless, and the supports at A and C are also frictionless. 01 F B nc 02 C (a) Assuming 0₁ = 26.0° and 0 2 = 51.0°, what are n and n? (Enter the magnitudes in N.) ΠΑ пс = = N N (b) The force any strut applies on a pin must be directed along the length of the strut as a force of tension or compression. What are the directions of the forces that the struts exert on the pins joining them? strut AB on joint A: ---Select--- strut AB on joint B: strut BC on joint B: strut BC on joint C: strut AC on joint A: strut AC on joint C: |---Select--- --Select--- --Select--- --Select--- |---Select--- ✓ ✓ ✓ Find the force of tension or of compression (in N) in each of the three struts. bar AB N N bar BC bar AC Narrow_forwardThe center of mass of the arm shown in the figure is at point A. Find the magnitudes (in N) of the tension force F+ and the force Fs which hold the arm in equilibrium. (Let = 22.5°.) Assume the weight of the arm is 34.8 N. N |Fsl N F 8.00 cm -29.0 cm iarrow_forwardHi, Please type the whole transcript correctly using comma and periods and as needed. Please mention the name of each scientist says. The picture of a video on YouTube has been uploaded down.arrow_forward
 Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Foundations of Astronomy (MindTap Course List)PhysicsISBN:9781337399920Author:Michael A. Seeds, Dana BackmanPublisher:Cengage Learning
Foundations of Astronomy (MindTap Course List)PhysicsISBN:9781337399920Author:Michael A. Seeds, Dana BackmanPublisher:Cengage Learning Stars and Galaxies (MindTap Course List)PhysicsISBN:9781337399944Author:Michael A. SeedsPublisher:Cengage Learning
Stars and Galaxies (MindTap Course List)PhysicsISBN:9781337399944Author:Michael A. SeedsPublisher:Cengage Learning






