
Interpretation:
Considering the depth of material, the concentration profile should be determined. Also, the graph for the profile P for pre-deposition process should be plotted.
Concept introduction:
Constant source diffusion is the relationship of diffusion source with depth, diffusion coefficient and time. The relationship is given by using the below equation,
Where,
D is the diffusion coefficient.
t is the time.
x is the depth.
Constant source diffusion is of two types:
- Pre deposition step: It is the first step for constant source diffusion in which a small quantity of impurity is doped using the constant source.
- Drive in deposition: It is the second step for constant source diffusion in which the material is maintaining the higher value of temperature for a certain period of time.
Equation used for calculating the diffusion is,
Fick's Law of diffusion: This law states that molar flux is directly proportional to concentration gradient. The law is stated as:
Where,
J is the molar flux defined as the number of atoms passing per unit area per unit time.
D is the diffusion coefficient in
Factors affection diffusion are as follows:
- Temperature
- Diffusion coefficient
The following equation is stated as:
Where,
Q is the activation energy in calorie/ mole.
R is universal gas constant in
T is the absolute temperature in kelvin.
Explanation of Solution
Given Information:
The given equation for basis is:
Where,
c is the concentration considering pre deposition function.
D is the diffusion coefficient.
X is the depth.
T is the time.
erf is the error function.
The given boundary conditions are:
Depth =
Concentration of P at depth of
The temperature at which material is conducted is
Value of diffusion coefficient is
Total time for carrying out the process is
Equation considered for calculation is,
On integrating the above equation within limits,
Thus, the equation considered for calculation is,
Assuming the various values of depth required for calculation. Assumed values of depth are,
Calculation of concentration with respect to time and depth. Considering depth as
Value of diffusion coefficient (D) is
Total time for carrying out the process is
Substituting the given value in the above relation,
Using table for calculation of error function,
Thus, concentration at a depth of
Calculation of concentration with respect to time and depth. Considering depth as
Value of diffusion coefficient (D) is
Total time for carrying out the process is
Substituting the given value in the above relation,
When the value of error function exceeds the range of limit 4. The formula used for calculation of error function is,
Thus, concentration at a depth of
Calculation of concentration with respect to time and depth. Considering depth as
Value of diffusion coefficient (D) is
Total time for carrying out the process is
Substituting the given value in the above relation,
When the value of error function exceeds the range of limit 4. The formula used for calculation of error function is,
Thus, concentration at a depth of
Calculation of concentration with respect to time and depth. Considering depth as
Value of diffusion coefficient (D) is
Total time for carrying out the process is
Substituting the given value in the above relation,
When the value of error function exceeds the range of limit 4. The formula used for calculation of error function is,
Thus, concentration at a depth of
Calculation of concentration with respect to time and depth. Considering depth as
Value of diffusion coefficient (D) is
Total time for carrying out the process is
Substituting the given value in the above relation,
When the value of error function exceeds the range of limit 4. The formula used for calculation of error function is,
Thus, concentration at a depth of
Calculation of concentration with respect to time and depth. Considering depth as
Value of diffusion coefficient (D) is
Total time for carrying out the process is
Substituting the given value in the above relation,
When the value of error function exceeds the range of limit 4. The formula used for calculation of error function is,
Thus, concentration at a depth of
Calculation of concentration with respect to time and depth. Considering depth as
Value of diffusion coefficient (D) is
Total time for carrying out the process is
Substituting the given value in the above relation,
When the value of error function exceeds the range of limit 4. The formula used for calculation of error function is,
Thus, concentration at a depth of
Calculation of concentration with respect to time and depth. Considering depth as
Value of diffusion coefficient (D) is
Total time for carrying out the process is
Substituting the given value in the above relation,
When the value of error function exceeds the range of limit 4. The formula used for calculation of error function is,
Thus, concentration at a depth of
Calculation of concentration with respect to time and depth. Considering depth as
Value of diffusion coefficient (D) is
Total time for carrying out the process is
Substituting the given value in the above relation,
When the value of error function exceeds the range of limit 4. The formula used for calculation of error function is,
Thus, concentration at a depth of
The table represents the data of concentration with variation in depth,
| Depth | Concentration |
Based on the given values drawing graph of concentration versus depth,
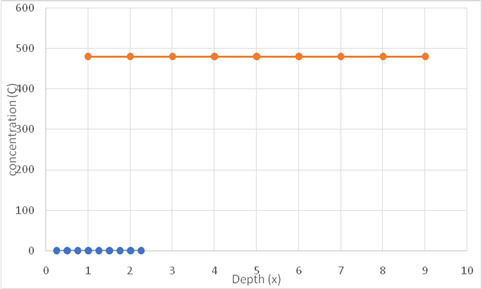
Thus, the required graph of concentration versus depth is shown above. As for pre deposition process concentration has dependency on time and depth, blue line is showing variation of concentration versus time and yellow line represents the variation of concentration with time.
Want to see more full solutions like this?
Chapter 5 Solutions
Essentials of Materials Science and Engineering, SI Edition
- This is an old practice exam, the answer is Ax = Az = 0, Ay = 2000, TDE = 4750, Cx = 2000, Cy = 2000, Cz = -800 but how?arrow_forwardDuring calibration of an LVDT, the data shown in the accompanying table were obtained. Using a spreadsheetprogram, plot the relation between the micrometer reading and voltage. What is the linear range of the LVDT? Determinethe calibration factor of the LVDT by obtaining the best fit line of the data within the linear range.arrow_forwardHydrogen, important for numerous processes, can be produced by the shift reaction: CO+H2O-CO2 +H2 In the reactor system shown in the Figure, the conditions of conversion have been adjusted so that the H2 content of the effluent from the reactor is 3 mol %. Based on the data in following figure: a. Calculate the composition of the fresh feed. b. Calculate the moles of recycle per mole of hydrogen produced. Recycle CO, H2O Feed CO H₂O Reactor % 3 mol % H₂ Separator % CO₂ 48 H₂ 48 CO 4arrow_forward
- Q2. Figure Q2 shows a block diagram with an input of C(s) and an output R(s). a) C(s) K₁ R(s) K2 1 + 5s 1+2s Figure Q2. Block diagram of control system. Simply the block diagram to get the transfer function of the system C(s)/R(s). b) What is the order of the system? c) What is the gain of the system? d) Determine the values of K₁ and K₂ to obtain a natural frequency w of 0.5 rad/s and damping ratio of 0.4. e) What is the rise time and overshoot of the system with a unit step input?arrow_forwardthis is an old practice exam, the answer is Fmin = 290.5lb but howarrow_forwardQ4. a) A purely derivative controller (i.e. with a zero at the origin only) is defined by an improper transfer function. Considering its asymptotic behaviour, explain why a purely derivative controller is difficult to implement in practice. Relate your explanation to the potential limitations on system performance. b) Discuss the potential issues faced by a control system with a large cut-off frequency. Relate your discussion to the implications on system performance. c) The transfer function of a lag compensator is given by 2 KPID(S) = 2.2++0.2s S By using the asymptotic approximation technique: (i) Obtain the standard form and corner frequency for each individual component of KPID(S). (ii) Clearly describe the asymptotic behaviour of each individual component of KPID(S).arrow_forward
- Module Code: EN2058 Q1. a) List the advantages and disadvantages of a closed loop system compared to an open loop system. b) c) What is the procedure for designing a control system for a bread toaster? An RC circuit is given in Figure Q1. vi(t) and v(t) are the input and output voltages. (i) Derive the transfer function of the circuit. (ii) With a unit step change vi(t) applied to the circuit, derive and sketch the time response of the circuit. R1 R2 v₁(t) R3 C1 vo(t) R₁ =R2 = 10 k R3 = 100 kn C₁ = 100 μF Figure Q1. RC circuit. (iii) Assuming zero initial conditions, obtain the impulse and ramp responses of the circuit from the step response derived in (ii). Sketching is not needed.arrow_forwardQ3. a) The frequency response method enables the study of the steady-state response of a system G(s). What type of inputs are used for frequency response? If the system is linear and stable, how does the output differ from the input? Compare the main characteristics of two types frequency response plots. b) Consider the control system shown in Figure Q3. Controller E(s) R(s) Desired output C(s) Plant G(s) Y(s) Actual output 3(s + 3) C(s) = k G(s) = = s(s - 1)(s + 10) Figure Q3. Closed-loop system. (i) Considering definitions in the study of bounded-input bounded-output stability, is G(s) stable? Classify the poles and zeros of G(s). (ii) G(s) defined in Figure Q3 is a system completely characterised by its transfer function. Explain why this is the case. (iii) Obtain the closed-loop transfer function P(s) = Y(s)/R(s) of the system. (iv) Based on your result for the previous question [Question 3b)-(iii)], use the Routh-Hurwitz stability criterion to determine suitable values of gain K…arrow_forwardThis is an exam review question. The answer is Pmin = 622.9 lb but whyarrow_forward
- Please do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forward
 MATLAB: An Introduction with ApplicationsEngineeringISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsEngineeringISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Essentials Of Materials Science And EngineeringEngineeringISBN:9781337385497Author:WRIGHT, Wendelin J.Publisher:Cengage,
Essentials Of Materials Science And EngineeringEngineeringISBN:9781337385497Author:WRIGHT, Wendelin J.Publisher:Cengage, Industrial Motor ControlEngineeringISBN:9781133691808Author:Stephen HermanPublisher:Cengage Learning
Industrial Motor ControlEngineeringISBN:9781133691808Author:Stephen HermanPublisher:Cengage Learning Basics Of Engineering EconomyEngineeringISBN:9780073376356Author:Leland Blank, Anthony TarquinPublisher:MCGRAW-HILL HIGHER EDUCATION
Basics Of Engineering EconomyEngineeringISBN:9780073376356Author:Leland Blank, Anthony TarquinPublisher:MCGRAW-HILL HIGHER EDUCATION Structural Steel Design (6th Edition)EngineeringISBN:9780134589657Author:Jack C. McCormac, Stephen F. CsernakPublisher:PEARSON
Structural Steel Design (6th Edition)EngineeringISBN:9780134589657Author:Jack C. McCormac, Stephen F. CsernakPublisher:PEARSON Fundamentals of Materials Science and Engineering...EngineeringISBN:9781119175483Author:William D. Callister Jr., David G. RethwischPublisher:WILEY
Fundamentals of Materials Science and Engineering...EngineeringISBN:9781119175483Author:William D. Callister Jr., David G. RethwischPublisher:WILEY





