ELEM PRIN OF CHEMICAL PROC(LL)+NEXTGEN
20th Edition
ISBN: 9781119761006
Author: FELDER
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 5, Problem 5.23P
Spray drying is a process in which a liquid containing dissolved or suspended solids is injected into a chamber through a spray nozzle or centrifugal disk atomizer. The resulting mist is contacted with hot air, which evaporates most or all of the liquid, leaving the dried solids to fall to a conveyor belt at the bottom of the chamber.
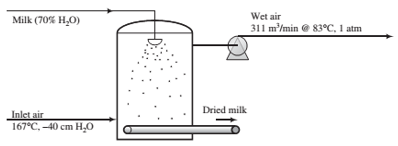
Powdered milk is produced in a spray dryer 6 m in diameter by 6 m high. Air enters at 167°C and −40 cm H2O. The milk fed to the atomizer contains 70% water by mass, all of which evaporates. The outlet gas contains 12 mole% water and leaves the chamber at 83°C and 1 atm (absolute) at a rate of 311 m3/min.
(a) Calculate the production rate of dried milk and the volumetric ?ow rate of the inlet air. Estimate the upward velocity of air (m/s) at the bottom of the dryer.
(b) Engineers often face the challenge of what to do to a process when demand fora product increases (or decreases). Suppose in the present case production must be doubled. (i) Why is it unlikely that the ?ow rates of feed and air can simply be increased to achieve the new production rate? (ii) An obvious option is to buy another dryer like the existing one and operate the two in parallel. Give two advantages and two disadvantages of this option. (m) Still another possibility is to buy a larger dryer to replace the original unit. Give two advantages and two disadvantages of doing so. Estimate the approximate dimensions of the larger unit.
Expert Solution & Answer
Learn your wayIncludes step-by-step video
schedule04:43
Students have asked these similar questions
#5 The irreversible liquid phase second order reaction, 2A → B, is carried out in a CSTR. The
entering concentration of A, CAD is 2 mol/L, and the exit concentration of A, CA is 0.1 mol/L. The
volumetric flow rate, vo, is at 3 L/s and is constant (v=vo). The reaction rate constant, k is 0.03
L/mol's. What is the corresponding reactor volume?
Problem 9.11 An 80 mm long line MN has its end M 15 mm in front of the V.P. The distance between
the ends projector is 50 mm. The front view is parallel to and 20 mm above reference line. Draw the
projections of the line and determine its inclination with the V.P. Also, locate the traces.
Interpretation Front view of a line is parallel to xy, therefore,
1. The line is parallel to the H.P.
2. The top view of the line has true length.
3. The front view has projected length equal to the distance be-
tween the projectors.
Construction
Refer to Fig. 9.11.
1. Draw a reference line xy. Mark point m' 20 mm above xy and
point m 15 mm below xy.
2. Draw a 50 mm long line m'n' parallel to xy.
3. Draw an arc with centre m and radius 80 mm to meet projec-
tor from point n' at point n. Join mn to represent the top view.
Determine its inclination with xy as the inclination of line MN
with the V.P. Here = 51°.
4. Traces Extend line mn to meet xy at point v. Project point v
to meet m'n' produced at…
oh
30
20
D
и
D
P
60
60
80
Chapter 5 Solutions
ELEM PRIN OF CHEMICAL PROC(LL)+NEXTGEN
Ch. 5 - A liquid mixture containing 40.0 wt% n-octane and...Ch. 5 - Prob. 5.2PCh. 5 - Prob. 5.3PCh. 5 - Prob. 5.4PCh. 5 - Prob. 5.5PCh. 5 - Prob. 5.6PCh. 5 - Prob. 5.7PCh. 5 - Prob. 5.8PCh. 5 - Prob. 5.9PCh. 5 - Prob. 5.10P
Ch. 5 - Prob. 5.11PCh. 5 - Prob. 5.12PCh. 5 - Prob. 5.13PCh. 5 - Prob. 5.14PCh. 5 - Prob. 5.15PCh. 5 - Prob. 5.16PCh. 5 - Prob. 5.17PCh. 5 - Prob. 5.18PCh. 5 - Prob. 5.19PCh. 5 - A device has been designed to measure the flow...Ch. 5 - Prob. 5.21PCh. 5 - Prob. 5.22PCh. 5 - Spray drying is a process in which a liquid...Ch. 5 - Prob. 5.24PCh. 5 - Lewis12 describes the hazards of breathing air...Ch. 5 - A stream of air at 35°C and a gauge pressure of...Ch. 5 - Prob. 5.27PCh. 5 - In froth ?otation, air is bubbled through an...Ch. 5 - Prob. 5.29PCh. 5 - Prob. 5.30PCh. 5 - Bread is typically made by ?rst dissolving...Ch. 5 - Prob. 5.32PCh. 5 - Prob. 5.33PCh. 5 - Prob. 5.34PCh. 5 - Prob. 5.35PCh. 5 - Prob. 5.36PCh. 5 - Prob. 5.37PCh. 5 - Prob. 5.38PCh. 5 - Prob. 5.39PCh. 5 - A spray-drying operation similar to that described...Ch. 5 - Prob. 5.41PCh. 5 - Fermentation is a biochemical process in which a...Ch. 5 - Prob. 5.43PCh. 5 - Prob. 5.44PCh. 5 - Ethane at 25°C and 1.1 atm (abs) flowing at a rate...Ch. 5 - The ?ow of air to a gas-?red boiler furnace is...Ch. 5 - Prob. 5.47PCh. 5 - The oxidation of nitric oxide NO+12O2NO2 takes...Ch. 5 - Prob. 5.49PCh. 5 - 5.50.19 In chemical vapor deposition (CVD), a...Ch. 5 - A gas turbine power plant receives a shipment of...Ch. 5 - Prob. 5.52PCh. 5 - 5.53.20 Chemicals are stored in a laboratory with...Ch. 5 - Prob. 5.54PCh. 5 - Prob. 5.55PCh. 5 - A stream of ho dry nitrogen flows through a...Ch. 5 - Prob. 5.57PCh. 5 - You have purchased a gas cylinder that is supposed...Ch. 5 - The current global reliance on fossil fuels for...Ch. 5 - Two humid gas streams are combined in a heated...Ch. 5 - Most of the concrete used in the construction of...Ch. 5 - The ultimate analysis of a No. 4 fuel oil is 86.47...Ch. 5 - A stream of liquid n-pentane flows at a rate of...Ch. 5 - Alka-Seltzer( is an over-the-counter medicine used...Ch. 5 - Hydrogen sul?de has the distinctive unpleasant...Ch. 5 - The quantity of sulfuric acid used globally places...Ch. 5 - A small power plant produces 500 MW of electricity...Ch. 5 - You have been assigned the task of measuring the...Ch. 5 - Prob. 5.69PCh. 5 - Methanol is synthesized from carbon monoxide and...Ch. 5 - Prob. 5.71PCh. 5 - Prob. 5.72PCh. 5 - Steam reforming is an important technology for...Ch. 5 - A ?owchart of a methanol synthesis process is...Ch. 5 - The measured volumetric flow rate of ethane at...Ch. 5 - Prob. 5.76PCh. 5 - Methanol is to be delivered to a process unit at a...Ch. 5 - Prob. 5.78PCh. 5 - Prob. 5.79PCh. 5 - Prob. 5.80PCh. 5 - Prob. 5.81PCh. 5 - Prob. 5.82PCh. 5 - Prob. 5.83PCh. 5 - Prob. 5.84PCh. 5 - Prob. 5.85PCh. 5 - Prob. 5.86PCh. 5 - Prob. 5.87PCh. 5 - Prob. 5.88PCh. 5 - Prob. 5.89PCh. 5 - A fuel cell is an electrochemical device that...Ch. 5 - In a metered-dose inhaler (MDI), such as those...Ch. 5 - Prob. 5.92PCh. 5 - Prob. 5.93PCh. 5 - Approximately 150 SCFM (standard cubic feet per...Ch. 5 - Prob. 5.95PCh. 5 - Prob. 5.96PCh. 5 - Prob. 5.97PCh. 5 - The product gas from a coal gasification plant...Ch. 5 - Prob. 5.99PCh. 5 - Prob. 5.100PCh. 5 - A gas mixture consisting of 15.0 mole% methane....Ch. 5 - A system has been devised to store acetonitrile...Ch. 5 - Prob. 5.103PCh. 5 - Prob. 5.104P
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
How does a computers main memory differ from its auxiliary memory?
Java: An Introduction to Problem Solving and Programming (8th Edition)
Why is the study of database technology important?
Database Concepts (8th Edition)
The solid steel shaft AC has a diameter of 25 mm and is supported by smooth bearings at D and E. It is coupled ...
Mechanics of Materials (10th Edition)
Assume a telephone signal travels through a cable at two-thirds the speed of light. How long does it take the s...
Electric Circuits. (11th Edition)
How are relationships between tables expressed in a relational database?
Modern Database Management
What is an uninitialized variable?
Starting Out with Programming Logic and Design (5th Edition) (What's New in Computer Science)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, chemical-engineering and related others by exploring similar questions and additional content below.Similar questions
- ⑤ b Δε m ab C 40arrow_forwardProblem 10.16 An isosceles triangle of base 40 mm and altitude 54 mm has its base in the V.P. The surface of the plane is inclined at 50° to the V.P. and perpendicular to the H.P. Draw its projections. Construction Refer to Fig. 10.17. An isosceles triangle has its base in the V.P., so con- sider that initially the triangle ABC is placed in the V.P. with base AB perpendicular to the H.P. 1. First stage Draw a triangle a'b'c' keeping a'b' perpendicular to xy to represent the front view. Project the corners to xy and obtain ac as the top view. 2. Second stage Reproduce the top view of first stage keeping ab on xy and ac inclined at 50° to xy. Obtain new points a', b' and c' in the front view by joining the points of intersection of the vertical projectors from a, b and c of the second stage with the corresponding horizontal locus lines from a', b' and c' of the first stage. Join a'b'c' to represent the final front view. Here, the front view is an equilateral triangle of side 40 mm. X 54…arrow_forward%9..+ ۱:۱۹ X خطأ عذرا ، الرقم الذي أدخلته خاطئ. يرجى إدخال رقم بطاقة الشحن الصالحة والمحاولة مرة أخرى. رصيد هاتفك قم بمسح الرمز = رقم بطاقة التعبئة 7794839909080 رمز مكون من 13 او 14 رقماً طريقة إعادة التعبئة قم باعادة تعبئة الرصيد إعادة تعبئة الإنترنت إعادة تعبئة الرصيد O >arrow_forward
- Problem 10.14 A hexagonal plane of side 30 mm has a corner in the V.P. The surface of the plane is inclined at 45° to the V.P. and perpendicular to the H.P. Draw its projections. Assume that the diagonal through the corner in the V.P. is parallel to the H.P. d' a 2 b b.f C' c.e b 'C' H.P. (a) V.P E HEX 30 e' O' d' a a' b' C' b' X y a b,f c,e d b,f (b) c,earrow_forwardProblem 10.18 A 60° set-square has the shortest edge of 40 mm lying in the V.P. The surface is in- clined to the V.P. and perpendicular to the H.P. such that the front view appears as an isosceles triangle. Draw the projections of the set-square and determine its inclination with the V.P. Construction Refer to Fig. 10.18. A 60° set-square inclined to the V.P. and per- pendicular to the H.P. can appear as an isosceles triangle in the front view, when the shorter edge is in the V.P. 1. First stage Draw a right angled triangle 40 a' a' b' c' b' X 40 C' a,b C a,b a'b'c' keeping 40 mm long a'b' perpen- dicular to xy. Project the corners to xy and obtain ac as the top view. 2. Second stage Draw another right angled triangle a'b'c' on the horizontal locus line from points a', b' and c' of the first stage such that length of b'c' is equal to that of a'b'. Project a'b' to meet xy at ab. Draw an arc with centre a and radius equal to ac of the first stage to meet the vertical projector of c' at…arrow_forward□ 40 a' 12 o' a O d'arrow_forwardTL = 85 D. Problem 9.12 The top view of a line measures 60 mm. The line is parallel to the V.P. and inclined at 45° to the H.P. One end of the line is 25 mm in front of the V.P. and lies on the H.P. Draw its projections and determine the true length. Interpretation Let the line be PQ parallel to the V.P. The front view has true length and the top view is parallel to xy. Construction Refer to Fig. 9.12. 1. Draw a reference line xy. Mark point p' on xy and point p 25 mm below xy. 2. Draw a 60 mm long line pq parallel to xy. This repre- sents the top view. 3. Draw line from point p', inclined at 45° to xy to meet the projector from point q at point q'. Join p'a' to represent the front view. Measure length of p'a' as true length of line PQ. Here T.L. = 85 mm. Result True length of line PQ is p'q' = 85 mm. 5 Fig. 9.12 p 60 σarrow_forwardProblem 9.13 A 70 mm long line PQ does not have H.T. and V.T. One end of the line is 30 mm in front of the V.P. and 20 mm above the H.P. Draw its projections. Interpretation As the line PQ does not have H.T. and V.T., it is parallel to both H.P. and V.P. Construction Refer to Fig. 9.13. 1. Draw a reference line xy. Mark point p' 20 mm above xy and point p 30 mm below xy. 2. Draw a 70 mm long line p'a' parallel to xy to repre- sent the front view. X 20 p Fig. 9.13 3. Also, draw a 70 mm long line pq parallel to xy to represent the top view. 70 q yarrow_forwardProblem 10.19 A square lamina ABCD of side 40 mm is suspended from a point O such that its surface is inclined at 30° to the V.P. The point O lies on the side AB 12 mm away from A. Draw its projections. Construction Refer to Fig. 10.19. 1. First stage Draw a square a'b'c'd keeping a'd' parallel to xy. Mark a point o' on a'ď at a distance 12 mm from end a' as the point of suspension. Also, mark the centre of the square g' to represent the centre of gravity. 2. Second stage Reproduce the front view of first stage such that o'g' is perpendicular to xy. Project corners and obtain bd as the top view. 3. Third stage Reproduce the top view keeping bd inclined at 30° to xy. Obtain new points a', b', c' and ď' in the front view by joining the points of intersection of the vertical projectors drawn from points a, b, c and d of the third stage with the corresponding horizontal locus lines drawn from points a', b', c' and ď of the second stage. Join new a'b'c'd to represent the final front view.arrow_forwardProblem 10.15 A circular plane of diameter 50 mm is resting on a point of the circumference on the V.P. The plane is inclined at 30° to the V.P. and the centre is 35 mm above the H.P. Draw its projections.arrow_forwardYou are asked to manufacture 10 kg of polyester with a number-average molecular weight of 1000 by polymerizing butane-1,4-diol(HO(CH2)4OH) with adipic acid (HOOC-(CH2)4-COOH).a) What weight of diol and diacid do you need, respectively? To whatextent, p, should the reaction be carried out to? Assume a stoichiometricbalance.b) What are the number and weight fractions of dimer, trimer and tetramerat this point in the reaction?c) Because of the polymerization by dehydration to olefin, 3 mol% of thediol will be lost. What would be the number-average molecular weightwhen the reaction is carried out to the same extent? How could you offsetthis loss so that the desired molecular weightarrow_forward9.4. A PID temperature controller is at steady state with an output pressure of 9 psig. The set point and process temperature are initially the same. At time = 0, the set point is increased at the rate of 0.5°F/min. The motion of the set point is in the direction of lower temperatures. If the current settings are PART 3 LINEAR CLOSED-LOOP SYSTEMS Ke = 2 psig/°F Ti = 1.25 min TD = 0.4 min plot the output pressure versus time.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education
Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning
Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The
Introduction to Chemical Engineering Thermodynami...
Chemical Engineering
ISBN:9781259696527
Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark Swihart
Publisher:McGraw-Hill Education
Elementary Principles of Chemical Processes, Bind...
Chemical Engineering
ISBN:9781118431221
Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. Bullard
Publisher:WILEY
Elements of Chemical Reaction Engineering (5th Ed...
Chemical Engineering
ISBN:9780133887518
Author:H. Scott Fogler
Publisher:Prentice Hall
Industrial Plastics: Theory and Applications
Chemical Engineering
ISBN:9781285061238
Author:Lokensgard, Erik
Publisher:Delmar Cengage Learning
Unit Operations of Chemical Engineering
Chemical Engineering
ISBN:9780072848236
Author:Warren McCabe, Julian C. Smith, Peter Harriott
Publisher:McGraw-Hill Companies, The