Practical Management Science
5th Edition
ISBN: 9781305734845
Author: WINSTON
Publisher: Cengage
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Chapter 5, Problem 42P
Summary Introduction
To determine: The way to minimize the total distance.
Introduction: In linear programming, the unbounded solution would occur when the objective function is infinite. If no solution satisfied the constraints, then it is said to be an unfeasible solution.
Expert Solution & Answer
Explanation of Solution
Determine the number of students in districts from each community:
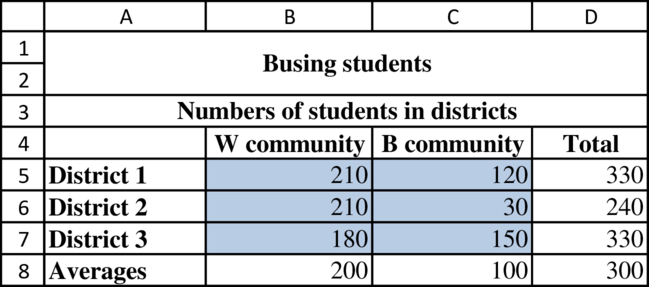
Determine the busing distance:
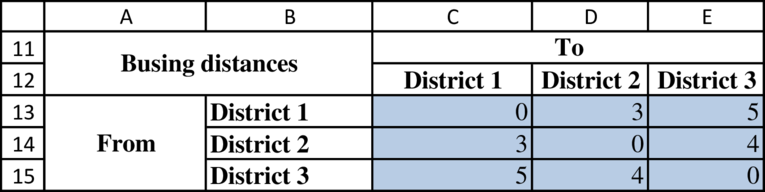
Determine the number of students on the bus from each community:
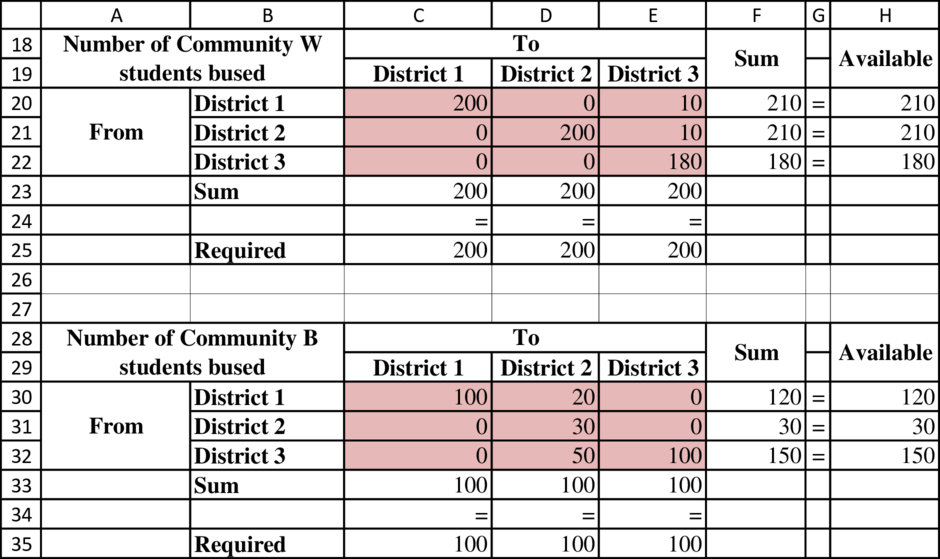
Determine the busing distances:
Formula to determine the number of students in districts from each community:
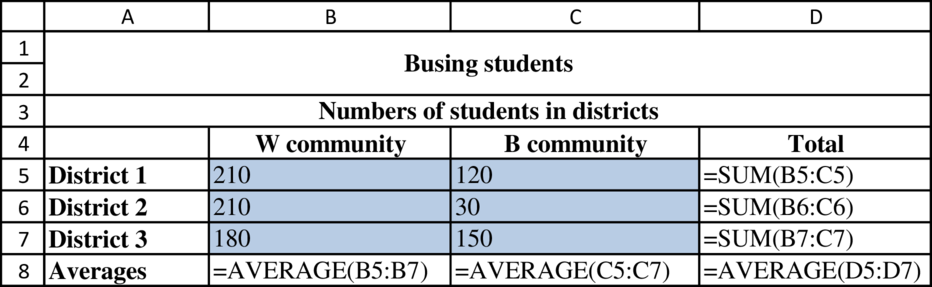
Formulae to determine the number of students in the bus from each community:
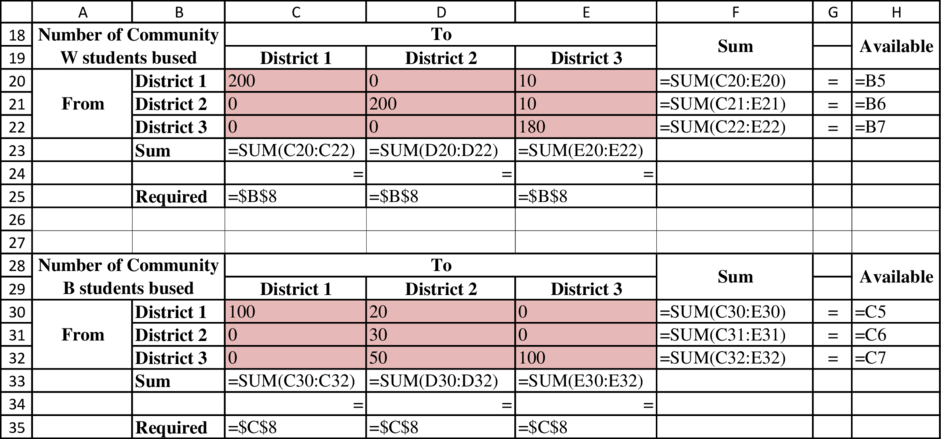
Formula to determine the busing distances:
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
A person starting in Columbus must visit Great Falls, Odessa, and Brownsville, and then return home to Columbus in one car trip. The road mileage between the cities is shown.
Columbus
Great Falls
Odessa
Brownsville
Columbus
---
102
79
56
Great Falls
102
---
47
69
Odessa
79
47
---
72
Brownsville
56
69
72
---
a)Draw a weighted graph that represents this problem in the space below. Use the first letter of the city when labeling each
b) Find the weight (distance) of the Hamiltonian circuit formed using the nearest neighbor algorithm. Give the vertices in the circuit in the order they are visited in the circuit as well as the total weight (distance) of the circuit.
The Hamilton County Local Government has eight sectors which need fire protection. Adequate
Fire protection can be provided in each sector either by building a fire station in that sector, or by
building a fire station in another sector which is no more than a 12-minute drive away. The time
to drive between the centers of each pair of sectors is given in the following table. (Because of
one-way streets and left turns the times are not symmetric.) The cost to build a fire station is the
same in each sector.
Formulate an integer programming model to choose which sectors should have their own fire station.
Solve the model by using Excel Solver.
Facility Location. A paper products manufacturer has enough capital to build and
manage some additional manufacturing plants in the United States in order to meet increased
demand in three cities: New York City, NY; Los Angeles, CA; and Topeka, KS. The company is
considering building in Denver, CO; Seattle, WA; and St. Louis, MO.
Max Operating
Capacity
400 tons/day
700 tons/day
Denver
Seattle
$10/ton
$17/tor
$5/ton
$11/ton....
$18/ton....
$28/ton
Los Angeles
Topeka
New York City
Figure 1: Graphical representation of the given data
=
• The cost fi of building plants in these cities is fi
$10,000,000 in Seattle.
Unmet Demand
300 tons/day
100 tons/day
500 tons/day
• Due to geographic constraints, plants in Denver and Seattle would have a maximum operating
capacity kį of 400 tons/day and 700 tons/day respectively.
$5,000,000 in Denver and f2
=
• The cost cij per ton of transporting paper from city i to city j is outlined in Figure 1.
• The unmet demand d, for Los Angeles, Topeka, and New…
Chapter 5 Solutions
Practical Management Science
Ch. 5.2 - Prob. 1PCh. 5.2 - Prob. 2PCh. 5.2 - Prob. 3PCh. 5.2 - Prob. 4PCh. 5.2 - Prob. 5PCh. 5.2 - Prob. 6PCh. 5.2 - Prob. 7PCh. 5.2 - Prob. 8PCh. 5.2 - Prob. 9PCh. 5.3 - Prob. 10P
Ch. 5.3 - Prob. 11PCh. 5.3 - Prob. 12PCh. 5.3 - Prob. 13PCh. 5.3 - Prob. 14PCh. 5.3 - Prob. 15PCh. 5.3 - Prob. 16PCh. 5.3 - Prob. 17PCh. 5.3 - Prob. 18PCh. 5.4 - Prob. 19PCh. 5.4 - Prob. 20PCh. 5.4 - Prob. 21PCh. 5.4 - Prob. 22PCh. 5.4 - Prob. 23PCh. 5.4 - Prob. 24PCh. 5.4 - Prob. 25PCh. 5.4 - Prob. 26PCh. 5.4 - Prob. 27PCh. 5.4 - Prob. 28PCh. 5.4 - Prob. 29PCh. 5.5 - Prob. 30PCh. 5.5 - Prob. 31PCh. 5.5 - Prob. 32PCh. 5.5 - Prob. 33PCh. 5.5 - Prob. 34PCh. 5.5 - Prob. 35PCh. 5.5 - Prob. 36PCh. 5.5 - Prob. 37PCh. 5.5 - Prob. 38PCh. 5 - Prob. 42PCh. 5 - Prob. 43PCh. 5 - Prob. 44PCh. 5 - Prob. 45PCh. 5 - Prob. 46PCh. 5 - Prob. 47PCh. 5 - Prob. 48PCh. 5 - Prob. 49PCh. 5 - Prob. 50PCh. 5 - Prob. 51PCh. 5 - Prob. 52PCh. 5 - Prob. 53PCh. 5 - Prob. 54PCh. 5 - Prob. 55PCh. 5 - Prob. 56PCh. 5 - Prob. 57PCh. 5 - Prob. 58PCh. 5 - Prob. 59PCh. 5 - Prob. 60PCh. 5 - Prob. 61PCh. 5 - Prob. 62PCh. 5 - Prob. 63PCh. 5 - Prob. 64PCh. 5 - Prob. 65PCh. 5 - Prob. 66PCh. 5 - Prob. 67PCh. 5 - Prob. 68PCh. 5 - Prob. 69PCh. 5 - Prob. 70PCh. 5 - Prob. 71PCh. 5 - Prob. 72PCh. 5 - Prob. 73PCh. 5 - Prob. 74PCh. 5 - Prob. 75PCh. 5 - Prob. 76PCh. 5 - Prob. 77PCh. 5 - Prob. 80PCh. 5 - Prob. 81PCh. 5 - Prob. 82PCh. 5 - Prob. 83PCh. 5 - Prob. 85PCh. 5 - Prob. 86PCh. 5 - Prob. 87PCh. 5 - Prob. 2C
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, operations-management and related others by exploring similar questions and additional content below.Similar questions
- Creative Robotics (CR) manufactures two lightweight robots designed for easier house-cleaning. The Alpha-ONE model is older, heavier, and is designed for carpet cleaning. The Alpha-TWO model is newer, lighter, and is designed primarily for wooden floor cleaning. The management team is trying to identify how to minimize the total costs of producing these two models. Their full-time workers consist of primarily manufacturing experts and about 3 people are required to commit themselves to manufacture the Alpha-ONE model and 4 for the Alpha-TWO model, per day. They have a total pool of 100 full-time workers now but are willing to hire more manufacturers if required. Similarly, the Alpha-TWO model is more complex and management has a pool of 20 part-time technical workers to help with the complexity, every day. Again, they are willing to hire more part-time workers if required to assist with the Alpha-TWO model. As far as staff allocations for additional assistance in manufacturing…arrow_forwardThe distance between two cities in the United States can be approximated by the following formula, where lat1 and long1 are the latitude and longitude of city 1 and lat2 and long2 are the latitude and longitude of city 2. 69 (lat1 − lat2)2 + (long1 − long2)2 Ted's daughter is getting married, and he is inviting relatives from 15 different locations in the United States. The file Wedding gives the longitude, latitude, and number of relatives in each of the 15 locations. Ted would like to find a wedding location that minimizes the demand-weighted distance, where demand is the number of relatives at each location. Assuming that the wedding can occur anywhere, find the latitude and longitude of the optimal location. (Hint: Notice that all longitude values given for this problem are negative. Make sure that you do not check the option for Make Unconstrained Variables Non-Negative in Solver. Round your answers to three decimal places.) latitude of the optimal wedding location:…arrow_forwardThe Janie Gioffre Drapery Company makes three types of draperies at two different locations. At location I, it can make 10 pairs of deluxe drapes, 20 pairs of better drapes, and 13 pairs of standard drapes per day. At location II, it can make 20 pairs of deluxe, 50 pairs of better, and 6 pairs of standard per day. The company has orders for 3000 pairs of deluxe drapes, 6300 pairs of better drapes, and 1800 pairs of standard drapes. If the daily costs are $750 per day at location I and $900 per day at location II, how many days should Janie schedule at each location to fill the orders at minimum cost? location I days location II days Find the minimum cost.$arrow_forward
- Show your step-by-step process using THE SPECIAL PURPOSE LINEAR PROGRAMMING: MODI TRANSPORTATION METHOD to solve this problem. XYZ Incorporated has received a contract to supply gravel to three new road projects located at three different locations. Project A needs 174 truckloads, Project B needs 204 truckloads, and Project C needs 143 truckloads. The company has three gravel warehouses located in three different places. Warehouse 1 has 158 truckloads available, warehouse 2 has 184, and warehouse 3 has 179. The cost of transportation from the warehouse to the projects are: from warehouse 1 to Projects A, B, C = Php 4, Php 8, Php 8 per truckload respectively. From warehouse 2 to Projects A, B, C = Php 16, Php 24, Php 16 per truckload respectively. From warehouse 3 to Projects A, B, C = Php 8, Php 16, Php 24 per truckload respectively. The objective is to design a plan of distribution that will Minimize the cost of transportation.arrow_forwardMonsters, Inc. has two plants for producing electricity, one in Monsterville and another is in New Yeti. The Monsterville plant produces according to eM(x1,x2) = min{xX1,2x2} and the New Yeti plant produces according to eNY(x1,x2) = min{2x1,x2}, where xi and x2 are the inputs. iii. How much of each input will the firm need in order to produce 20 units electricity in the New Yeti plant? iv. Assume now that Monsters, Inc. decides to produce 40 units of electricity and it can split production in any manner between the two plants. Is the technology available to this firm convex or concave? Explain your answer.arrow_forwardA fertilizer manufacturer has to fulfill supply contracts to its two main customers (650 tons to Customer A and 800 tons to Customer B). It can meet this demand by shipping existing inventory from any of its three warehouses. Warehouse 1 has 400 tons of inventory onhand, Warehouse 2 (W2) has 500 tons, and Warehouse 3 (W3) has 600 tons. The company would like to arrange the shipping for the lowest cost possible, where the per-ton transit costs are as follows: W 1 W 2 W 3 $7.50 $6.75 $6.25 $7.00 $6.50 $8.00 Customer A Customer B Write the objective function and the constraint in equations. Let V;= tons shipped to customer i from warehouse j, and so on. For example, VA1 = tons shipped to customer A from warehouse W1. This exercise contains only parts b, c, d, e, and f. b) The objective function for the LP model = Minimize Z = $7.50 + $6.25 + $6.50 (shipping cost to customer A) V + $6.75 + $7.00 + $8.00 (shipping cost to customer B) c) Subject to: Customer A's demand Customer B's demand…arrow_forward
- A retail store in Des Moines, Iowa, receives shipments of a particular product from KansasCity and Minneapolis. Let x 5 number of units of the product received from Kansas City y 5 number of units of the product received from Minneapolisa. Write an expression for the total number of units of the product received by the retail store in Des Moines. b. Shipments from Kansas City cost $0.20 per unit, and shipments from Minneapolis cost$0.25 per unit. Develop an objective function representing the total cost of shipments to Des Moines. c. Assuming the monthly demand at the retail store is 5000 units, develop a constraint that requires 5000 units to be shipped to Des Moines. d. No more than 4000 units can be shipped from Kansas City, and no more than 3000 units can be shipped from Minneapolis in a month. Develop constraints to model this situation. e. Of course, negative amounts cannot be shipped. Combine the objective function and constraints developed to state a mathematical model…arrow_forwardA health Centre will be built to serve 7 communities. The geographical location of the communities and their population is shown in the table below. Communities A, X =2.5 (km), Y=4.5(km), Population( 000's)=2 Communities B, X =2.5 (km), Y=2.5(km), Population( 000's)=5 Communities C, X =5.5 (km), Y=4.5(km), Population( 000's)=10 Communities D, X =5 (km), Y=2(km), Population( 000's)=7 Communities E, X =8 (km), Y=5(km), Population( 000's)=10 Communities F, X =7 (km), Y=2(km), Population( 000's)=20 Communities G, X =9 (km), Y=2.5(km), Population( 000's)=14 There is a possibility of building the Centre in two communities, community C and F. Based on the Demand-Distance criterion what is your recommendation for the site of the Centre. The distances to be measured based on Rectilinear method. Based on…arrow_forwardTMA manufactures 37-in. high definition LCD televisions in two separate locations, Locations I and II. The output at Location I is at most 6000 televisions/month, whereas the output at Location II is at most 5000 televisions/month. TMA is the main supplier of televisions to the Pulsar Corporation, its holding company, which has priority in having all its requirements met. In a certain month, Pulsar placed orders for 3000 and 4000 televisions to be shipped to two of its factories located in City A and City B, respectively. The shipping costs (in dollars) per television from the two TMA plants to the two Pulsar factories are as follows. To Pulsar Factories From TMA City A City B Location I $6 $3 Location II $7 $8 TMA will ship x televisions from Location I to city A and y televisions from Location I to city B. Find a shipping schedule that meets the requirements of both companies while keeping costs to a minimum. (x, y) = 2000,4000…arrow_forward
- Consider the following network representation of a transportation problem:arrow_forwardWhat factors determine whether a person chooses car or bus to travel to work? That is an interesting question. Suppose that you analyze this simple transportation problem using the probit model. The variables in the model are defined as follows: autotime commute time via auto, minutes commute time via bus, minutes =(bus time - auto time)/10, 10 minute units = 1 if auto chosen bustime dtime auto The probit model you estimate is P(AUTO = 1) = ¤(ß1 + B2DTIME). The estimates of the parameters are: -0.0788 + 0.400DTIME. The marginal effect of increasing public (bus) transportation time, given that travel via public transportation currently takes 15 minutes longer than auto travel is A) 0.348 B) 0.139 C) 0.307 D) 0.123 E) None of the above (A, B, C, D) is close to be correct.arrow_forwardThere are two companies manufacturing drones. Company A manufactures mass market drones, while company B manufactures customised drones according to customers’ requirements. In 2020, company A produces 3,200 drones, 3% of which were found to be defective and cannot pass the quality check. Company A employs 5 workers working an average of 8 hours a day in the drone production, and they worked 200 working days in 2020.In contrast, company B produces 900 drones, 10% of which were found to be defective and cannot pass the quality check. Company B employs 3 workers working an average of 6 hours a day in the drone production, and they worked 170 days in 2020. (a) If the drone manufacturing is seen as a process, what is considered as the output of the production processes of companies A and B and why? (b) Measure the single-factor manpower productivity for the two companies. (c) Is it reasonable to compare the manpower productivity of the two companies and reach a conclusion that one company…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management Science
Operations Management
ISBN:9781337406659
Author:WINSTON, Wayne L.
Publisher:Cengage,