
Concept explainers
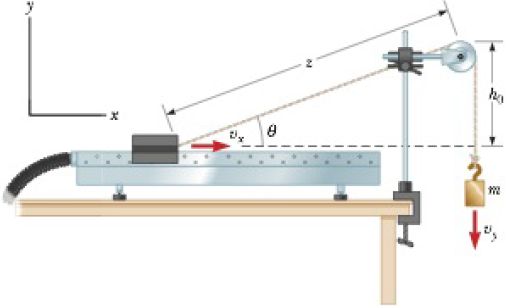
A 1.00-kg glider on a horizontal air track is pulled by a string at an angle θ. The taut string runs over a pulley and is attached to a hanging object of mass 0.500 kg as shown in Figure P5.40. (a) Show that the speed vx of the glider and the speed vy of the hanging object are related by vx = uvy, where u = z(z2 − h02)−1/2. (b) The glider is released from rest. Show that at that instant the acceleration ax of the glider and the acceleration ay of the hanging object are related by ax = uay. (c) Find the tension in the string at the instant the glider is released for h0 = 80.0 cm and θ = 30.0°.
Figure P5.40
(a)
The relation between the speed of the glider and the speed of the hanging object.
Answer to Problem 40AP
The relation between the speed of the glider and the speed of the hanging object is
Explanation of Solution
The mass of the glider is
The free body diagram of the given case is as shown below.
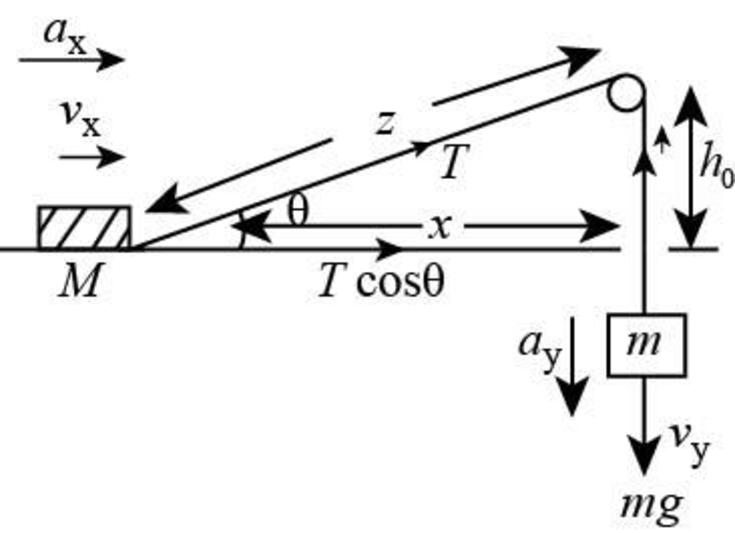
Figure (1)
Form the above figure (1).
Write the expression for the length of the string using Pythagorean Theorem,
Here,
Rearrange the above equation for
Write the expression for the speed of the glider
Here,
Substitute
The term
Write the expression for the speed of the hanging object.
Here,
Substitute
Substitute
Conclusion:
Therefore, the relation between the speed of the glider and the speed of the hanging object is
(b)
The relation between the acceleration of the glider and the speed of the hanging object.
Answer to Problem 40AP
The relation between the acceleration of the glider and the speed of the hanging object is
Explanation of Solution
From equation (2), the relation of
Write the expression for the acceleration of the glider
Substitute
The initial velocity of the hanging object is zero.
Substitute
Here,
Conclusion:
Therefore, the relation between the acceleration of the glider and the speed of the hanging object is
(c)
The tension of the string.
Answer to Problem 40AP
The tension of the string is
Explanation of Solution
From the free body diagram in figure (1) the net direction in
From part (a) the value of
Substitute
Substitute
Thus, the value of
The net force in
Here,
Substitute
Rearrange the above equation for
The net force in the
Here,
Form part (b) substitute
From equation (3) substitute
Conclusion:
Substitute
Therefore, the tension in the string is
Want to see more full solutions like this?
Chapter 5 Solutions
Physics for Scientists and Engineers, Volume 2
- 8. With the aid of a diagram draw the following electric circuit and use the resistor as the load, (a) Closed circuit (b) Open circuitarrow_forwardLab 8 Part 3 PHET Wave Interface simulation. I am having trouble with this part of the lab.arrow_forwardMick and Rick are twins born on Earth in the year 2175. Rick grows up to be an Earth-bound robotics technician while Mick becomes an intergalactic astronaut. Mick leaves the Earth on his first space mission in the year 2200 and travels, according to his clock, for 10 years at a speed of 0.75c. Unfortunately, at this point in his journey, the structure of his ship undergoes mechanical breakdown and the ship explodes. How old is Rick when his brother dies?arrow_forward
 Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning





