
Determine the real roots of
(a) Graphically.
(b) Using the
(c) Using three iterations of the bisection method to determine the highest root. Employ initial guesses of
Compute the estimated error
(a)
The real roots of the equation
Answer to Problem 1P
Solution:
The real roots of the equation are
Explanation of Solution
Given Information:
The equation
Calculation:
The graph of the function can be plotted using MATLAB.
Code:
Output:
This gives the following plot:
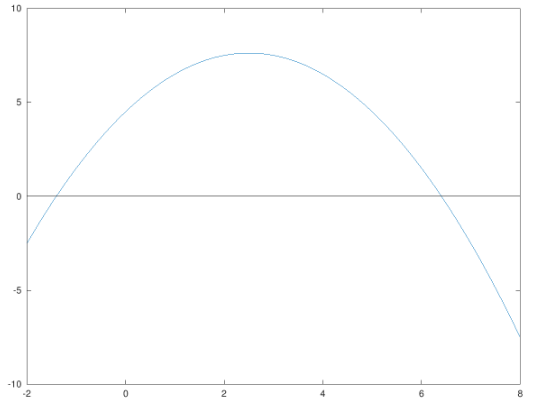
The roots of an equation can be represented graphically by the x-coordinate of the point where the graph cuts the x-axis. From the plot, the two zeros of the equation can be approximated as
(b)
To calculate: The real roots of the equation
Answer to Problem 1P
Solution:
The roots of the equation are
Explanation of Solution
Given Information:
The equation
Formula Used:
The roots of an equation
Calculation:
Consider the provided equation,
Now substitute
Thus, the roots of the equation are
(c)
To calculate: The highest root of the equation
Answer to Problem 1P
Solution:
The highest root of the equation can be approximated as 6.875. The true and approximate errors are as follows:
Explanation of Solution
Given Information:
The equation
Formula Used:
A root of an equation can be obtained using the bisection method as follows:
1. Choose 2 values x, say a and b such that
2. Now, estimate the root by
3. If,
Calculation:
For the provided function:
Hence,
Now take the first root to be,
As, the true root computed from part (b) was 6.40512484. Now, the true relative percentage error would be:
The true error is 17.1%. There would be no approximate error for the first iteration.
Now,
Thus,
Now, the second root would be:
As, the true root computed from part (b) was 6.40512484. Now, the true relative percentage error would be:
The true error is 2.42%.
The approximate error can be computed as:
The approximate error is 2%.
Now,
Thus,
Now, the third root would be:
As, the true root computed from part (b) was 6.40512484. Now, the true relative percentage error would be:
The true error is 7.34%.
The approximate error can be computed as:
The approximate error is 9.09%.
Thus, the highest root can be approximated as 6.875.
Want to see more full solutions like this?
Chapter 5 Solutions
Numerical Methods for Engineers
- 18) Find all the complex cube roots of -2i. Leave your answers in polar form with the argument in degrees.arrow_forward9) Write an equation for the hyperbola. 2+ -6-5-4-3-2 -2- -4- -5+ + 23 45 6xarrow_forward8) Find an equation for the hyperbola with vertices at vertices at (±7, 0) and foci at (±9, 0).arrow_forward
- 3) Find an equation for the parabola with a vertex at (1, 2) and focus at (1, 4). A) (x - 1)² = 8(y-2) C) (x - 1)² = -8(y - 2) B) (y - 2)² = -12(x − 1) - D) (y - 2)² = 12(x-1)arrow_forward2) Graph the equation. y² = 12x 5 10 -10 -5 5 + 10 xarrow_forward15) Solve the triangles if possible. B = 11°, b = 15.5, a = 40.62arrow_forward
- 10) Find the exact value of the expression. tan−1 [tan (~ 7}]] 8arrow_forward12) The point (-15, -8) is on the terminal side of an angle in standard position. Determine the exact values of the three trigonometric functions sine, cosine, and tangent of the angle 0.arrow_forward6) Find the center, foci, and vertices of the ellipse. = 9 49 1arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage




