
Determine the real roots of
(a) Graphically.
(b) Using the
(c) Using three iterations of the bisection method to determine the highest root. Employ initial guesses of
Compute the estimated error
(a)
The real roots of the equation
Answer to Problem 1P
Solution:
The real roots of the equation are
Explanation of Solution
Given Information:
The equation
Calculation:
The graph of the function can be plotted using MATLAB.
Code:
Output:
This gives the following plot:
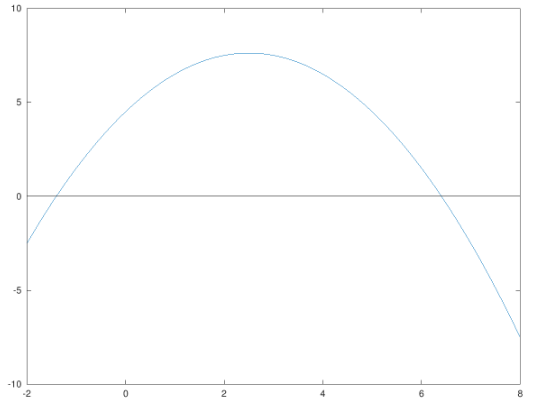
The roots of an equation can be represented graphically by the x-coordinate of the point where the graph cuts the x-axis. From the plot, the two zeros of the equation can be approximated as
(b)
To calculate: The real roots of the equation
Answer to Problem 1P
Solution:
The roots of the equation are
Explanation of Solution
Given Information:
The equation
Formula Used:
The roots of an equation
Calculation:
Consider the provided equation,
Now substitute
Thus, the roots of the equation are
(c)
To calculate: The highest root of the equation
Answer to Problem 1P
Solution:
The highest root of the equation can be approximated as 6.875. The true and approximate errors are as follows:
Explanation of Solution
Given Information:
The equation
Formula Used:
A root of an equation can be obtained using the bisection method as follows:
1. Choose 2 values x, say a and b such that
2. Now, estimate the root by
3. If,
Calculation:
For the provided function:
Hence,
Now take the first root to be,
As, the true root computed from part (b) was 6.40512484. Now, the true relative percentage error would be:
The true error is 17.1%. There would be no approximate error for the first iteration.
Now,
Thus,
Now, the second root would be:
As, the true root computed from part (b) was 6.40512484. Now, the true relative percentage error would be:
The true error is 2.42%.
The approximate error can be computed as:
The approximate error is 2%.
Now,
Thus,
Now, the third root would be:
As, the true root computed from part (b) was 6.40512484. Now, the true relative percentage error would be:
The true error is 7.34%.
The approximate error can be computed as:
The approximate error is 9.09%.
Thus, the highest root can be approximated as 6.875.
Want to see more full solutions like this?
Chapter 5 Solutions
Numerical Methods for Engineers
- the set of all preimages of 2 isarrow_forwardWhich diagram(s) represent the following relationships An injective function from A to B? A surjective function from A to B? An injective function from B to A? A surjective function from B to A?arrow_forwardDetermine if each statement is true or false. If the statement is false, provide a brief explanation: a) There exists x = R such that √x2 = -x. b) Let A = {x = ZIx = 1 (mod 3)} and B = {x = ZIx is odd}. Then A and B are disjoint. c) Let A and B be subsets of a universal set U. If x = A and x/ € A - B,then x = An B.| E d) Let f : RR be defined by f (x) = 1 x + 2 1. Then f is surjective.arrow_forward
- Write the negation of the definition of an injective functionarrow_forwardLet U= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {xeU Ix is a multiple of 3}, and B = {x = UIx = 0 (mod 2)}. Use the roster method to list all elements in each of the following sets: a) A, b) B, c) A u B, d) B – A, e) A^cn Barrow_forwardThe function f is; Injective (only), Surjective (only), Bijective, or none? show workarrow_forward
- For each a Є Z, if a ‡0 (mod 3), then a² = 1 (mod 3).arrow_forwardfind: f(3)=? , and the set of all preimages of 2 is ?arrow_forwardConstruct tables showing the values of alI the Dirichlet characters mod k fork = 8,9, and 10. (please show me result in a table and the equation in mathematical format.)arrow_forward
- Example: For what odd primes p is 11 a quadratic residue modulo p? Solution: This is really asking "when is (11 | p) =1?" First, 11 = 3 (mod 4). To use LQR, consider two cases p = 1 or 3 (mod 4): p=1 We have 1 = (11 | p) = (p | 11), so p is a quadratic residue modulo 11. By brute force: 121, 224, 3² = 9, 4² = 5, 5² = 3 (mod 11) so the quadratic residues mod 11 are 1,3,4,5,9. Using CRT for p = 1 (mod 4) & p = 1,3,4,5,9 (mod 11). p = 1 (mod 4) & p = 1 (mod 11 gives p 1 (mod 44). p = 1 (mod 4) & p = 3 (mod 11) gives p25 (mod 44). p = 1 (mod 4) & p = 4 (mod 11) gives p=37 (mod 44). p = 1 (mod 4) & p = 5 (mod 11) gives p 5 (mod 44). p = 1 (mod 4) & p=9 (mod 11) gives p 9 (mod 44). So p =1,5,9,25,37 (mod 44).arrow_forwardhow to construct the following same table?arrow_forwardplease work out more details give the solution.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage




